1.1.4. Частотная характеристика стационарных линейных динамических систем

Ниже будет показано, что для линейных стационарных систем при гармоническом входном сигнале, представляющем собой колебание с определенной амплитудой и частотой, их выход в установившемся режиме также будет представлять собой гармонический сигнал той же частоты. Частотная характеристика (ЧХ) линейной стационарной системы и является той функцией, которая позволяет найти параметры выходного гармонического сигнала по известным параметрам входного сигнала.

Прежде чем пояснить процедуру нахождения ЧХ, напомним, что всякое комплексное число может быть представлено в так называемой геометрической форме

,

где – модуль, а – фаза (аргумент) комплексного числа, определяемая из условий , . Так как , , то . Таким образом, поскольку

, (1.1.25)

гармонический сигнал с частотой может быть представлен как

, , (1.1.26)

где – постоянный вектор, определяющий амплитуду сигнала.

Заметим, что частотная характеристика, так же как и ПФ, соответствует описанию линейной стационарной системы по схеме «входвыход», при котором не требуется ее представление в форме пространства состояний (1.1.14), (1.1.15). Однако при разъяснении смысла ПФ в методическом плане удобно считать, что такое описание задано. Итак, предположем, что входной сигнал в уравнении (1.1.14) задан с помощью соотношения (1.1.26), и отыскивать частное решение этого уравнения будем в аналогичном виде

. (1.1.27)

Взяв производную от этого выражения и приравняв ее к правой части (1.1.14), с учетом вида (1.1.26) получим

, (1.1.28)

т.е. .

Отсюда с очевидностью следует, что если в (1.1.27) удовлетворяет соотношению

,

то (1.1.28) превращается в тождество, и функция

(1.1.29)

будет частным решением уравнения (1.1.14).

Выходной гармонический сигнал, таким образом, может быть записан как

, (1.1.30)

где функция

(1.1.31)

и определяет частотную характеристику [26,с.54] или частотную передаточную функцию [7,с.61] для системы (1.1.14), (1.1.15). В общем случае эта функция является матричной. Элементы (1.1.31) задают ЧХ, определяющие связь между соответствующими входами и выходами. Для системы с одним входом и выходом, используя геометрическую форму комплексного числа, можно записать

. (1.1.32)

Таким образом, для выходного сигнала будет справедливо представление в виде

или .

Из этого выражения и вытекает тот факт, что при наличии на входе системы гармонического колебания с амплитудой , частотой и нулевой начальной фазой на выходе будет гармоническое колебание с той же частотой, амплитудой и фазой .

Из сказанного следует, что ЧХ при скалярных входном и выходном сигналах представляет собой комплексное число, модуль которого равен отношению амплитуд выходного сигнала к амплитуде входной величины, а аргумент определяет сдвиг фаз выходного сигнала по отношению к входному. Функции и соответственно называются амплитудно-частотной и фазочастотной характеристиками [52, с.50].

Сопоставляя (1.1.20) и (1.1.31), нетрудно заметить, что ЧХ системы совпадает с ПФ, в которой комплексная переменная заменена на чисто мнимую величину

. (1.1.33)

Это соотношение и будем рассматривать как определение частотной характеристики, когда не предполагается задание системы в пространстве состояний.

Обращаем внимание, что частное решение (1.1.29) соответствует ненулевым начальным условиям, поскольку выходной сигнал в начальный момент времени не равен нулю и его значение определяется как

.

В сущности, это есть следствие того, что интегралы, задаваемые выражениями вида и , помимо чисто гармонической составляющей содержат еще одну составляющую, которую и необходимо скомпенсировать за счет соответствующего выбора начальных условий, для того чтобы в выходном сигнале была только гармоническая составляющая.

Таким образом, частотная характеристика в отличие от передаточной функции, во-первых, определяет связь выходного гармонического сигнала с входным гармоническим сигналом во временной области и, во-вторых, начальные условия не предполагаются нулевыми. Более подробно это обсуждается в примере 1.1.3. Нередко особенность, связанная с ненулевыми начальными условиями, упускается из виду, поскольку при введении ЧХ, как правило, подразумевается установившийся режим для асимптотически устойчивой системы, когда начальные условия не влияют на выходной сигнал. Напомним, что для асимптотически устойчивой линейной стационарной системы действительные части всех корней характеристического уравнения меньше нуля (см. подраздел 1.1.7).

 Пример 1.1.3. Получим частотную, амплитудно-частотную и фазочастотную характеристики для апериодического звена первого порядка и с их использованием – выражение на выходе при входном гармоническом сигнале, которое сопоставим с решением, приведенным в примере 1.1.1.

Принимая во внимание соотношения (1.1.24) и (1.1.33), запишем

.

Для получения представления ЧХ в виде (1.1.32) умножим и разделим на число , комплексно-сопряженное знаменателю

.

Отсюда следует, что выражения для амплитудно-частотной и фазочастотной характеристик примут вид (рис. 1.1.5)

, .

а)

б)

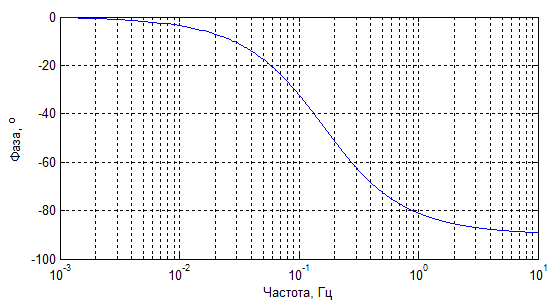
Рис. 1.1.5. Графики амплитудно-частотной (а) и фазочастотной (б) характеристик апериодического звена первого порядка

Задавая входной гармонический сигнал в виде , на выходе в соответствии с (1.1.31) получаем

(1.1.34)

Согласно результатам примера 1.1.1 при наличии входного воздействия выход будет иметь вид

,

где , т.е.

. (1.1.35)

Таким образом, видно, что выходные сигналы системы (1.1.34), (1.1.35) при одном и том же входном воздействии не совпадают друг с другом. Это объясняется той особенностью ЧХ, о которой шла речь выше. Выход (1.1.35) получен при нулевых начальных условиях, при этом помимо гармонической он имеет еще вторую составляющую. Выход же в виде (1.1.34) соответствует чисто гармоническому сигналу. Из (1.1.35) следует, что такой вид сигнала может быть только при начальном условии

.

Именно этому начальному условию и соответствует выражение (1.1.34), поскольку

. (1.1.36)

В случае устойчивой системы, т.е. при , второе слагаемое в (1.1.35) при увеличении времени стремится к нулю, и выражения (1.1.34) и (1.1.35) совпадают. 

Обратим внимание, что до сих пор при обсуждении понятия частотной характеристики не привлекалось преобразование Фурье. Более того, ЧХ была введена как функция, устанавливающая взаимосвязь выходного и входного сигналов во временной области. Нередко, однако, её определяют как отношение преобразований Фурье для выходного и входного сигналов либо как преобразование Фурье от весовой функции.

В связи с этим сделаем два замечания.

З а м е ч а н и е 1. В том случае, когда ЧХ вводится как отношение преобразований Фурье для выходного и входного сигналов [7, c.62] (см. задачу 1.1.4), необходимо помнить, что функции, для которых отыскиваются преобразования Фурье, должны быть абсолютно интегрируемыми.

З а м е ч а н и е 2. В случае, когда ЧХ определяется как преобразование Фурье от весовой функции, т.е. [7, c.62; 52, с.49]

,

требованию абсолютной интегрируемости должна также удовлетворять и весовая функция, что, как правило, имеет место для асимптотически устойчивых систем. Справедливость приведенного соотношения следует из того факта, что ПФ представляет собой преобразование Лапласа для весовой функции – выражение (1.1.21).

Поскольку весовая функция физически реализуемой системы отлична от нуля только при , то, как следует из результатов, приведенных в приложении П1.2, преобразование Фурье совпадет с преобразованием Лапласа при замене аргумента на . Однако в ряде же случаев приходится сталкиваться с ситуациями, когда при обсуждаемом варианте определения ЧХ требуется находить интеграл Фурье для функций, не удовлетворяющих условию абсолютной интегрируемости. Несмотря на некорректность выполняемых операций, в ряде случаев такой формальный подход приводит к справедливым результатам (см. комментарий к табл. П1.1 и пример, рассмотренный в задаче 1.1.5).