1.1.2. Определение выхода линейных динамических систем с помощью фундаментальной матрицы и весовой функции

Пусть задана линейная динамическая система:

; (1.1.7)

, (1.1.8)

в которой не разделяются входное возмущение и управление и считается, что задан некоторый входной сигнал , а ошибки измерения отсутствуют. Используя выражение (П2.8), нетрудно записать соотношение, связывающее выход системы с ее входом

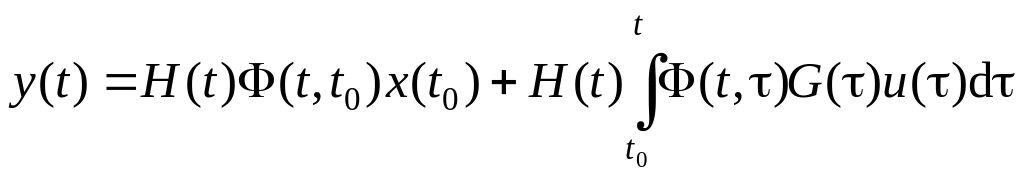, (1.1.9)

в котором – задаваемая с помощью соотношения (П2.7) фундаментальная матрица для уравнения (1.1.7). Таким образом, описание выхода системы в этом случае осуществляется по схеме: вход – состояние – выход [41, 42].

Первое слагаемое, порожденное начальным условием, нередко называют свободным движением системы

, (1.1.10)

а второе

, (1.1.11)

порожденное входным воздействием, – вынужденным движением системы.

В случае если начальные условия нулевые, выход системы определяется как

,(1.1.12)

где

. (1.1.13)

Функция , задаваемая этим соотношением называется весовой функцией или функцией веса [7]. Такое название следует из того, что в правой части последнего выражения определяет в каждый момент времени на интервале от до уровень вклада входного воздействия в выходной сигнал. В этом легко убедиться, если, вводя интервал дискретизации , записать приближенное представление выходного сигнала , где , , .

В общем случае представляет собой матрицу размерности , поэтому ее называют весовой матрицей [38]. В частном случае, когда и – единичные матрицы, весовая функция и фундаментальная матрица между собой совпадают.

Рассмотрим теперь стационарную систему:

; (1.1.14)

. (1.1.15)

Поскольку фундаментальная матрица для этой системы зависит от разности аргументов, то и весовая функция также будет зависеть лишь от разности аргументов, т.е. , или при

. (1.1.16)

В этом случае связь выхода стационарной системы с входным воздействием при нулевых начальных условиях будет определяться как

. (1.1.17)

Выражение такого типа называется сверткой функций, и в данном случае это функции и .

Заметим, что для весовой функции используют также термин – импульсная переходная функция [26]. Это название объясняется следующим образом. Пусть при нулевых начальных условиях входной сигнал представляет собой импульсное входное воздействие – воздействие в виде дельта-функции в момент по -му входу и при нулевых входных воздействиях по другим входам, т.е.

.

Определим -й выход системы. Для этого зададим матрицу , отсюда следует, что

,

где – -й элемент матрицы [7, с. 59].

Если входное воздействие в виде дельта-функции поступает в момент , т.е. , то в соответствии со свойствами дельта-функции выход системы примет вид

.

Таким образом, элемент представляет реакцию системы на -м выходе при импульсном входном воздействии в виде дельта-функции в начальный момент времени по -му входу при нулевых начальных условиях и нулевых входных воздействиях по другим входам.

Следует заметить, что весовая функция в выражении (1.1.17) отлична от нуля лишь при значениях аргумента, больших либо равных нулю, т.е. при . Это обусловлено тем, что весовая функция (1.1.16) соответствует физически реализуемой системе (1.1.14) (иногда говорят о реализуемой весовой функции или системе без упреждения), т.е. системе, в которой при формировании ее выходного сигнала (1.1.17) в текущий момент времени используются значения входного сигнала только в предшествующие моменты времени (рис. 1.1.1).

Рис. 1.1.1. Формирование выходного сигнала в физически-реализуемой системе, т.е. при

В противоположность этому для физически нереализуемой системы весовая функция отлична от нуля и при отрицательных значениях аргумента, т.е. . Следует заметить, что термин физически нереализуемая система носит условный характер, поскольку такая система на самом деле реализуема. Речь идет лишь о невозможности ее реализации в реальном масштабе времени. В частности, для рассматриваемых в дальнейшем устройств оценивания это означает, что при получении оценки в текущий момент времени используются не только прошлые, но и будущие измерения, что характерно при решении задач сглаживания или интерполяции. Эта ситуация поясняется на рис. 1.1.2.

Рис. 1.1.2. Формирование выходного сигнала в физически нереализуемой системе, т.е. при

 Пример 1.1.1. Пусть система скалярная, и ее модель задана в виде:

; .

Приведем выражения для весовой матрицы и с ее помощью найдем выход системы в случае, когда и .

Ясно, что для этого примера , , . Принимая во внимание (1.1.13) и (П2.15), можем записать: .

Рис. 1.1.3. График весовой функции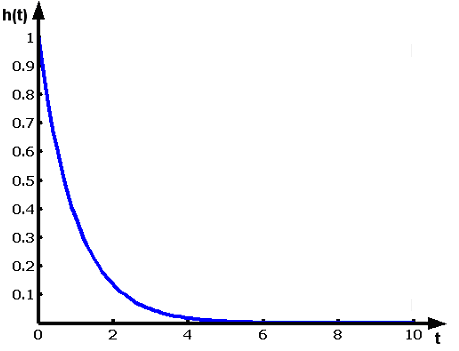

Пример графика весовой функции при и для рассматриваемой системы изображен на рис.1.1.3.

Представим выход системы в виде суммы

,

в которой первое слагаемое обусловлено начальным условием, а второе – порождено входным воздействием.

Принимая во внимание тот факт, что [14, с.118]

,

при получаем

=

.

Вводя , , , можем записать

,

где .

Таким образом,

.

Поскольку [Двайт, с.118]

,

при выход будет определяться как

.

Если параметр , то при на выходе имеем только гармоническую составляющую. То же самое будет при любом , если . 