Задачи к разделу

Задача 1.1.1. Убедитесь, что для матрицы вида (1.1.46) при и для характеристического многочлена справедливо представление

.

Задача 1.1.2. Для системы с передаточной функцией

запишите представление в пространстве состояния с использованием управляемой и наблюдаемой канонических форм.

Задача 1.1.3. Убедитесь в том, что для системы изображение по Лапласу для фундаментальной матрицы определяется как

.

Р е ш е н и е. Запишем выходной сигнал системы при нулевых начальных условиях в виде

.

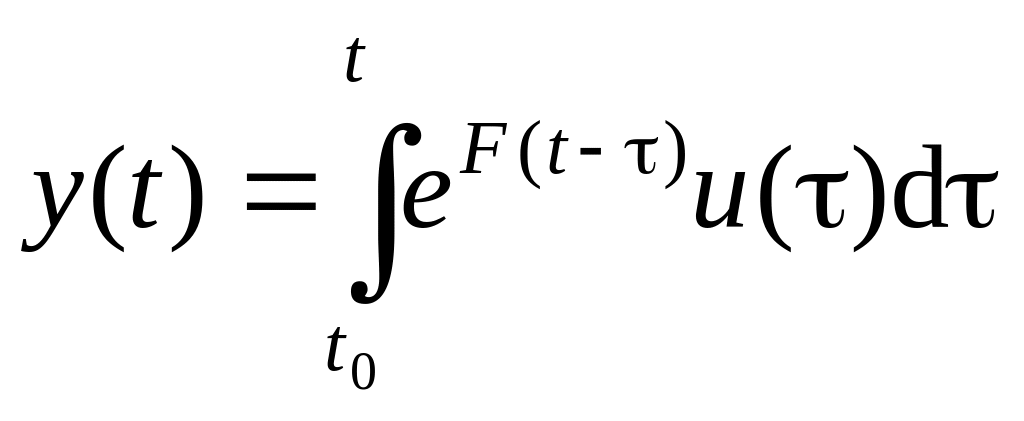Применяя преобразование Лапласа, получаем

.

Отсюда с очевидность следует, что

.

Задача 1.1.4. Покажите, что ЧХ может быть определена, как отношение преобразований Фурье для выходного и входного сигналов.

Р е ш е н и е. Полагая, что входной сигнал имеет вид (1.1.26) при , т.е. , и используя таблицу П1.1, запишем для него преобразование Фурье

.

Принимая во внимание вид выходного сигнала , можем записать преобразование Фурье

.

Отсюда с очевидностью следует, что отношение преобразований Фурье выходного и входного сигналов и представляет собой выражение для ПФ, задаваемое соотношением (1.1.32).

Задача 1.1.5. Найдите весовую и передаточную функцию и частотную характеристику для системы, заданной в виде

.

Р е ш е н и е. Весовая функция очевидно равна единице, поскольку в данном случае согласно (1.1.13) (при t>0). Передаточная функция и частотная характеристика определятся как

, .

Для получения представления ЧХ в виде (1.1.32) умножим и разделим на число, комплексно-сопряженное знаменателю, т.е.

.

Отсюда следует, что выражения для амплитудно-частотной и фазочастотной характеристик могут быть записаны как (рис. 1.1.3)

, .

Графики этих функций представлены на рис. 1.1.6.

Рассматриваемая система представляет собой обычный интегратор, при прохождении через который амплитуда гармонического сигнала уменьшается в раз, а фаза меняется на 90 градусов.

Заметим, что весовая функция в рассматриваемом случае не является абсолютно интегрируемой. Тем не менее, учитывая связь преобразований Лапласа и Фурье и тот факт, что при , нетрудно убедиться в том, что . Таким образом, в рассматриваемом примере ЧХ также может быть введена как преобразование Фурье от этой функции.

a)

б)

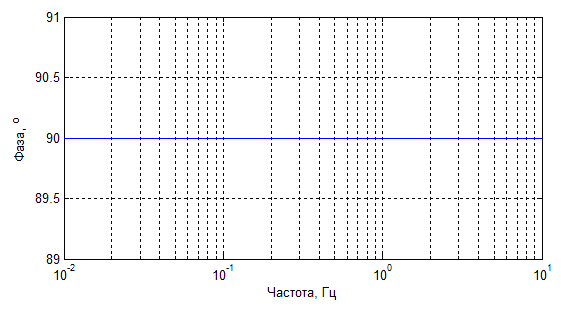
Рис. 1.1.6. Графики амплитудно-частотной (a) и фазочастотной характеристик (б)

Задача 1.1.6. Найдите ЧХ и весовую функцию для системы

Р е ш е н и е. С учетом результатов примера 1.1.4 легко получить ПФ в виде . Таким образом, . Вычисляя обратное преобразование Лапласа, получаем

.

Поскольку эта функция абсолютно интегрируема, то преобразование Фурье для этой функции с учетом того, что она отлична от нуля только при , будет совпадать с выражением для ЧХ. Нетрудно заметить, что рассматриваемое уравнение соответствует случаю 4 из примера П5 приложения 2, т.е. ( ), а , так что

,

Таким образом, в рассматриваемой системе всегда присутствуют незатухающие колебания. Например, при нулевом входном воздействии и , .

В общем случае такие колебания в двухмерной системе возникают всегда, когда матрица динамики системы может быть представлена как

.

Уравнения, порождающие более сложные гармонические колебания, рассматриваются, например, в [41, 42].

Задача 1.1.7. Покажите, что коэффициенты ошибок могут быть получены с помощью следующего соотношения [87, с.119]

,

Р е ш е н и е. Дифференцируя соотношение (1.1.21), можем записать

.

Отсюда вытекает

,

что и подтверждает справедливость (1.1.64).

Задача 1.1.8. Убедитесь в том, что для системы с ПФ , при выполнении условий , , система обладает астатизмом второго порядка.