1.1.5. Взаимосвязь между основными функциями, используемыми при описании линейных динамических систем
Введенные в предыдущих разделах функции, используемые для описания поведения динамических систем, могут быть сведены в табл. 1.1.1.
Т а б л и ц а 1.1.1
Основные функции, используемые при описании линейных систем
Название функции |
Обозначение |
Назначение |
Примечание |
Фундаментальная матрица |
|
Определяет общее решение
|
Используется как для стационарных, так и нестационарных систем |
Весовая функция, (импульсная переходная функция) |
|
Устанавливает связь выхода и входа при нулевых начальных условиях:
|
|
Передаточная функция |
|
Устанавливает связь изображений выхода и входа:
|
Используется для стационарных систем |
Частотная характеристика |
|
Устанавливает связь гармонических колебаний на выходе и входе:
|
,
.
,
.
,
.
Взаимосвязь между этими функциями для случая стационарных линейных систем отражается в табл. 1.1.2.
Т а б л и ц а 1.1.2
Взаимосвязь различных функций, используемых для описания поведения линейных стационарных систем
,
Отыски-ваемая функция |
Задаваемая функция |
|||
|
|
|
|
|
|
|
* |
* |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В
табл. 1.1.2 использованы обозначения,
введенные в приложении 1 для прямых
(
,
)
и обратных
,
преобразований
Фурье и Лапласа.
На диагонали этой таблицы приведены выражения, которые можно трактовать как исходные определения соответствующих функций для рассматриваемого класса систем, а вне диагонали – выражения, устанавливающие взаимосвязь между ними.
Следует
также отметить, что выражение
,
определяющее тот факт, что ЧХ может быть
найдена как преобразование Фурье от
весовой функции, следует воспринимать
с учетом замечания, приведенного в конце
подраздела 1.1.4.
Звездочка * в верхней графе означает, что не существует однозначного соответствия между задаваемыми и отыскиваемыми функциями. Так, например, зная ПФ, невозможно однозначно описать систему в форме пространства состояния. Причины отсутствия такого перехода обсуждаются в следующем подразделе.
1.1.6. Определение модели линейной динамической системы в пространстве состояний по заданной передаточной функции
Ранее предполагалось, что в качестве исходного описания системы задано ее представление в форме пространства состояния. При решении прикладных задач нередко возникает необходимость получить модель системы в пространстве состояния, располагая ее передаточной функцией. Обсудим этот вопрос более подробно.
Передаточной функции (1.1.22) соответствует уравнение, записанное в операторной форме, т.е. с помощью преобразования Лапласа
(1.1.37)
Во временной области этому уравнению можно однозначно сопоставить дифференциальное уравнение с постоянными коэффициентами -го порядка
(1.1.38)
Специфика этого уравнения заключается в том, что в правой части у него содержатся q-е производные от входного воздействия. Суть обсуждаемой задачи заключается в получении системы в форме Коши с помощью передаточной функции. Задача определения уравнений состояния по ПФ сводится к известной в теории дифференциальных уравнений задаче приведения линейных уравнений n-го порядка к системе уравнений в нормальной форме Коши [1, 2]. Простейший пример решения этой задачи рассмотрен в приложении 2 (пример 6).
Заметим, что решение задачи приведения линейных уравнений n-го порядка к системе уравнений в нормальной форме Коши неоднозначно, т.е. одной ПФ соответствует множество описаний системы в пространстве состояний в виде (1.1.14), (1.1.15). Покажем это.
Пусть задана ПФ
,
соответствующая системе (1.1.14), (1.1.15). С
использованием невырожденной, не
зависящей от времени
матрицы
,
введем новую переменную
. (1.1.39)
Поскольку
и
,
а следовательно,
,
можем записать
.
Или
.
Выход системы с новой переменной связан как
.
Вычисляя ПФ для преобразованной системы, имеем
Таким образом, для системы, имеющей ПФ , имеем новое описание в виде:
; (1.1.40)
, (1.1.41)
в котором ,
,
,
.
(1.1.42)
Преобразование называется преобразованием базиса, а , как отмечается в [73, с. 455], преобразованием подобия. Очевидно, что существует бесконечное множество преобразований подобия. Поскольку ПФ систем, связанных преобразованием подобия, совпадают, то каждой ПФ также соответствует бесконечное множество описаний в пространстве состояний. Следует также иметь в виду, что одной и той же ПФ, кроме того, могут соответствовать различные описания в пространстве состояний, не связанные между собой преобразованием подобия [1, с. 50].
Пример 1.1.4. Проиллюстрируем неоднозначность представления системы с заданной ПФ в пространстве состояний на примере системы, имеющей ПФ
,
(1.1.43)
в
которой
– круговая частота.
Рассмотрим систему, задаваемую уравнениями:
(1.1.44)
.
Поскольку
в этом случае
,
,
,
то с использованием (1.1.19) нетрудно
убедиться в том, что ПФ для этой системы
имеет вид (1.1.43).
Введя
преобразование
с матрицей
и используя (1.1.41), получим следующее
представление:
(1.1.45)
,
в
котором
,
,
.
Легко убедиться, что и для этой системы ПФ также имеет вид (1.1.43).
Рассмотрим два наиболее важных варианта получения описания системы в пространстве состояния для SISO-системы, ПФ которой задана в виде (1.1.22).
Первый вариант основан на использовании так называемой управляемой канонической формы для системы в пространстве состояния, для которой матрицы, определяющие описание системы записываются как [1]:
;
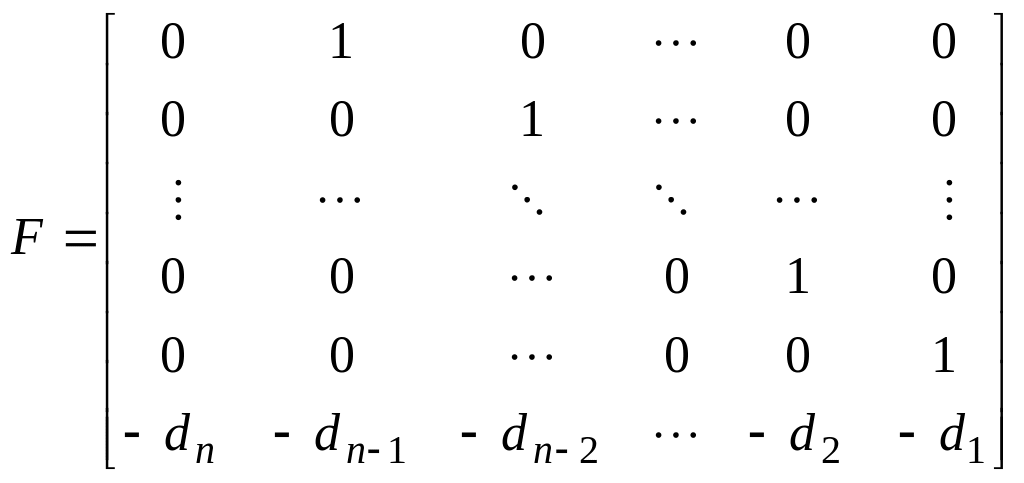(1.1.46)
,
.
(1.1.47)
Этим матрицам соответствуют уравнения:
(1.1.48)
.
(1.1.49)
Матрица (1.1.46) называется матрицей Фробениуса. Нетрудно убедиться в том, что соответствующий ей характеристический полином, определяемый из уравнения , задается следующим соотношением:
.
Иными словами, стоящие на последней
строке элементы матрицы
представляют собой коэффициенты
характеристического полинома.
Используя (1.1.20), можно показать, что для системы (1.1.48), (1.1.49) ПФ будет задаваться выражением (1.1.22).
Пример 1.1.5. Убедимся в справедливости приведенного утверждения на двухмерном примере, т.е. когда
,
,
.(1.1.50)
Используя эти
соотношения и выражения (1.1.20), (П2.28) для
ПФ и матрицы
,
запишем
,
откуда с очевидностью следует
. (1.1.51)
Особенность приведенного варианта получения описания системы в пространстве состояний заключаются в том, что входное воздействие присутствует в правой части уравнения только для последней компоненты вектора состояния, а выходной сигнал формируется в виде линейной комбинации компонент вектора состояния. Рассмотрим другой вариант получения описания системы в пространстве состояния для SISO-системы, ПФ которой задана в виде (1.1.22).
Этот вариант основан на использовании
наблюдаемой канонической формы,
для которой матрица динамики имеет вид
(1.1.46), а матрицы
и
записываются как
Элементы
матрицы
вычисляются через коэффициенты
многочленов
методом неопределенных коэффициентов.
Можно также использовать следующую
рекуррентную формулу
Этим матрицам соответствуют уравнения:
(1.1.52)
И в этом случае легко убедиться, что для такой системы передаточная функция будет задаваться выражением (1.1.22).
Особенность второго варианта представления системы в пространстве состояний с ПФ вида (1.1.22) заключается в том, что одно и тоже входное воздействие присутствует в правых частях уравнений для всех компонент вектора состояний, а выход системы соответствует его первой компоненте.
Пример 1.1.6. Убедимся в справедливости приведенного утверждения на примере системы второго порядка, т.е. покажем, что при
;
;
(1.1.53)
передаточная функция будет иметь вид (1.1.51).
Используя эти соотношения и выражения (1.1.20), (П2.28) для ПФ и матрицы , запишем
.
Откуда с очевидностью получаем (1.1.51).
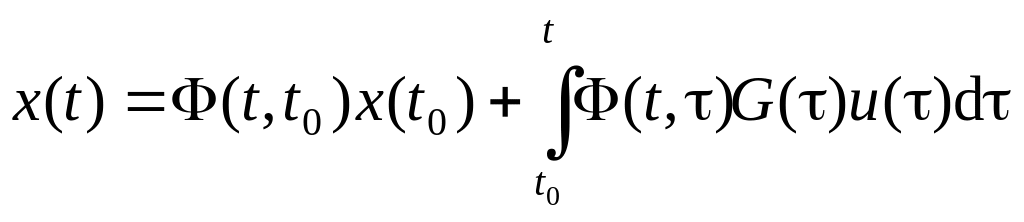
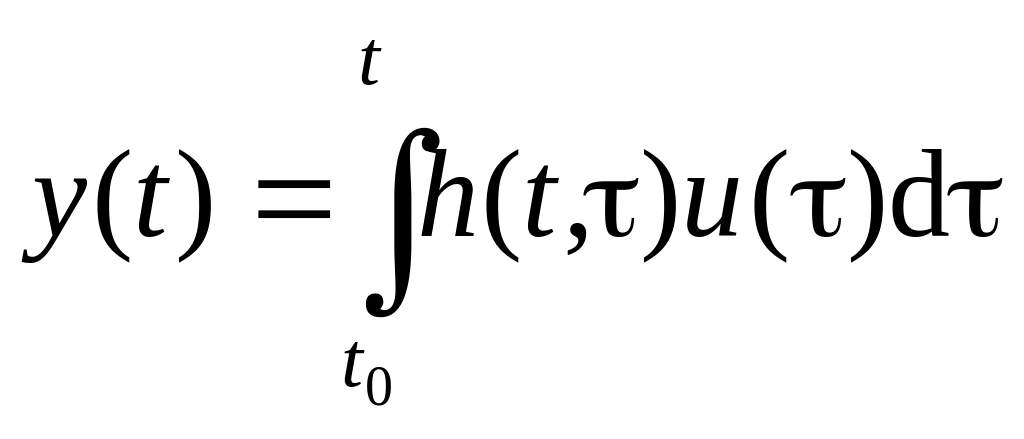