1.1.3. Передаточная функция стационарных линейных динамических систем

Передаточной функцией (ПФ) называется такая функция, которая определяет связь выходного и входного изображений по Лапласу при нулевых начальных условиях, т.е.

. (1.1.18)

Заметим, что в общем случае это определение не предполагает введение понятия состояния, и выход системы описывается как функция от входа, т.е. в данном случае описание системы осуществляется по схеме вход – выход [41, 42]. В то же время, располагая представлением системы в виде (1.1.14), (1.1.15), можно легко получить выражение для ПФ. Действительно, используя представление (П2.23) для общего решения при нулевых начальных условиях, можем записать выражение, связывающее входное и выходное изображения

. (1.1.19)

Таким образом, для ПФ получаем

. (1.1.20)

Сопоставляя (1.1.17) и (1.1.18), с учетом теоремы о свертке (см. приложение 2) нетрудно заметить, что передаточная функция представляет собой преобразование Лапласа от весовой функции , т.е.

, (1.1.21)

и соответственно, весовая функция стационарной системы может рассматриваться как оригинал от ПФ. В общем случае ПФ, так же, как и весовая функция, является матрицей, элементы которой определяют ПФ, устанавливающую связь между -м входом и -м выходом. Каждый элемент такой матрицы может быть представлен в виде отношений двух полиномов. В частности, для системы с одним входом и одним выходом можно записать следующее представление:

, (1.1.22)

где коэффициенты полинома, стоящего в знаменателе, совпадают с коэффициентами характеристического многочлена матрицы F, определяемым как . Такой вид ПФ следует из (1.1.20) и правила определения обратной матрицы (П1.1.21), приведенного в [73].

Заметим, что наряду с представлением (1.1.22) ПФ может быть задана и в виде

, (1.1.23)

где – обобщенный коэффициент передачи системы, а , – корни полиномов, называемые нулями и полюсами системы.

 Пример 1.1.2. Найдем ПФ для системы из примера 1.1.1 и определим с ее помощью реакцию системы на входной единичный скачок при нулевых начальных условиях.

ПФ в этом случае имеет вид

. (1.1.24)

Используя (1.1.18) и табл. П1.2, запишем

.

Отсюда получаем

.

Пример графика, иллюстрирующего реакцию системы с ПФ (1.1.24) на входной единичный скачок при и , представлен на рис. 1.1.4.

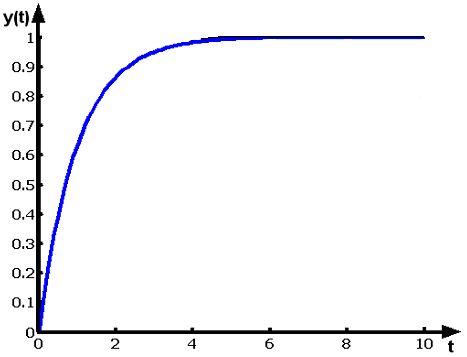
Рис. 1.1.4. Реакция системы с ПФ (1.1.24) на входной единичный скачок

Система с ПФ (1.1.24) в классической теории автоматического управления называется апериодическим звеном первого порядка. Величина называется постоянной времени. Такое название объясняется тем, что с ее помощью можно оценить время переходного процесса, за которое при , и решение становится существенно меньшим . Так, при и получаем , а . Обычно это время оценивается на уровне (3-5)T. 

Поскольку в общем случае описание системы с помощью ПФ может быть и не связано с ее представлением в виде (1.1.14), (1.1.15), важно оговорить, что степень числителя в (1.1.22) должна быть меньше степени знаменателя, т.е. . Если , то в выражении для ПФ можно выделить составляющие , . Их наличие, в свою очередь порождает наличие разрывных (физически неосуществимых) составляющих в весовой функции , поскольку эта функция есть оригинал от ПФ (табл. П1.2). К примеру, при , содержит дельта функцию. Системы такого типа называются физически неосуществимыми [87, c.107].

З а м е ч а н и е. Несмотря на то что при определении ПФ начальные условия предполагаются нулевыми, ясно, что, применяя преобразование Лапласа к уравнениям (1.1.14), (1.1.15), можно получить преобразование Лапласа для выходного сигнала с учетом ненулевых начальных условий.

Действительно, с учетом правил дифференцирования оригинала, приведенного в табл. П1.2, можем записать .