1.3. Дискретизация и моделирование линейных

динамических систем

В этом разделе рассматривается задача перехода от непрерывной динамической системы к ее дискретному аналогу, обсуждаются методы описания линейных стационарных систем в специальном наборе подпрограмм Control System Toolbox и анализируются особенности реализации процедуры дискретизации стационарных систем в пакете прикладных программ Matlab.

1.3.1. Дискретизация непрерывных систем

При исследовании динамических систем с использованием средств вычислительной техники важной является задача получения эквивалентного дискретного описания, или задача дискретизации непрерывных динамических систем [2, с.134; 99, 100], которая в простейшем случае может быть сформулирована следующим образом.

Задана математическая модель непрерывной динамической системы

, (1.3.1)

где и  векторы размерности и ,  известные матрицы соответствующей размерности.

Требуется найти такую дискретную систему, описываемую с помощью разностного уравнения

(1.3.2)

состояние которой при выполнении условий , совпадало бы с состоянием непрерывной системы в дискретные моменты времени , т.е.

, (1.3.3)

где , – интервал дискретизации.

Суть таким образом сформулированной задачи дискретизации заключается в нахождении матриц , , обеспечивающих выполнение (1.3.3) при сделанных предположениях.

Принимая во внимание соотношение (П2.8), для системы (1.3.1) можем записать

. (1.3.4)

Очевидно, что для совпадения первого слагаемого правой части (1.3.2) с соответствующим слагаемым (1.3.4) матрицу следует выбирать так, чтобы

. (1.3.5)

Предположим далее, что интервал дискретизации выбран из условия, при котором

, , (1.3.6)

т.е. в пределах интервала дискретизации можно считать, что входное воздействие постоянно

, . (1.3.7)

Тогда

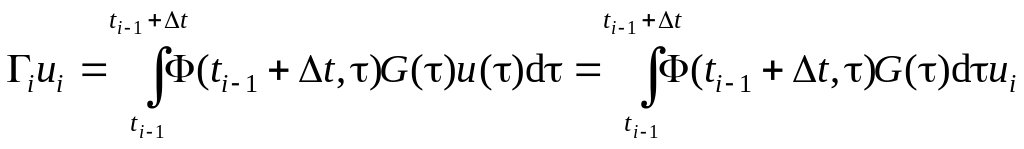.(1.3.8)

Отсюда с очевидностью следует, что для выполнения (1.3.3) матрица может быть найдена как

. (1.3.9)

Привлечение условия (1.3.6) соответствует использованию так называемого экстраполятора или фиксатора нулевого порядка (zero order hold-ZOH). В этом случае проблема дискретизации при использовании ZOH сводится к отысканию фундаментальной матрицы (1.3.5) и вычислению интеграла (1.3.9).

Рассмотрим частный случай стационарной системы, когда матрицы в выражении (1.3.1), а следовательно, и в (1.3.2) постоянны и не зависят от времени, т.е. .

В этой ситуации (1.3.5), (1.3.9) могут быть представлены как:

; (1.3.10)

. (1.3.11)

Последнее соотношение получается после введения замены .

В стационарном случае для вычисления фундаментальной матрицы можно использовать ее представление в виде ряда, тогда вместо (1.3.10) и (1.3.11) получаем:

; (1.3.12)

. (1.3.13)

Заметим, что если ввести

, (1.3.14)

то и будут иметь вид

; . (1.3.15)

Обычно при вычислениях используют

, (1.3.16)

так что

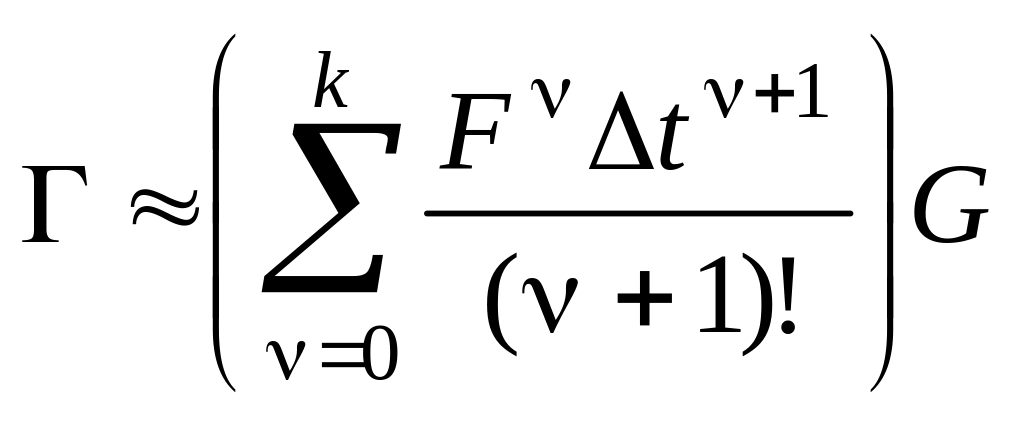; . (1.3.17)

Очевидно, что точность дискретизации, во-первых, зависит от того, насколько обосновано приближение (1.3.7), что существенно определяется величиной интервала , а, во-вторых, зависит от точности вычисления матриц (1.3.12), (1.3.13).

Нетрудно понять, что в стационарном случае достаточно один раз вычислить матрицы для дискретной модели, которые могут быть использованы для любого дискретного момента времени . Для нестационарных систем дискретизацию требуется проводить на каждом шаге. При этом следует иметь в виду, что для нестационарного случая интервал дискретизации необходимо выбирать так, чтобы помимо (1.3.7) можно было бы считать справедливыми следующие приближения:

, , . (1.3.18)

,

где – максимальное по модулю собственное число матрицы динамики , а коэффициент принимается равным 0,10,2.

Таким образом, к ошибкам дискретизации, обусловленным ошибками вычисления матричной экспоненты и ошибками приближения (1.3.7), добавляются методические ошибки, порожденные приближением (1.3.18).

Следует обратить внимание на тот факт, что представление фундаментальной матрицы с помощью ряда (1.3.12) и вытекающие из него формулы не являются экономичными с вычислительной точки зрения. Существует несколько методов, направленных на сокращение объема вычислений, при сохранении точности, в частности простейший и модифицированный методы Эйлера, методы Паде и Тастина [2, с. 142].