1.2.4. Модель микромеханического гироскопа

В настоящее время при построении современных инерциальных навигационных систем широкое применение находят микромеханические гироскопы и акселерометры [19, 53, 54, 58]. Рассмотрим (рис. 1.2.4) модель для так называемого микромеханического гироскопа (ММГ) RR-типа (от англ. rotate-rotate) [59, с. 103].

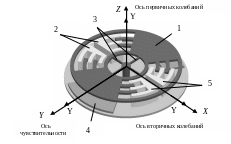
Рис. 1.2.4. Микромеханический гироскоп RR-типа

1  ротор, 2  неподвижные гребенчатые структуры привода первичных колебаний вокруг оси Z; 3  упругие балки подвеса; 4  датчик угла вокруг оси X; 5  неподвижные гребенчатые структуры датчика угла вокруг оси Z

Принцип действия гироскопа заключается в следующем. При помощи специальной системы управления возбуждаются и поддерживаются на заданном уровне первичные угловые колебания ротора 1 относительно оси Z (главная ось или ось первичных колебаний). После появления подлежащей определению угловой скорости вокруг оси чувствительности Y возникает момент сил Кориолиса, величина которого определяется как , где  значение кинетического момента ротора. Момент вызывает так называемые вторичные угловые колебания ротора гироскопа относительно оси X (ось прецессии или ось вторичных колебаний).

Измеряя величину вторичных колебаний ротора, можно определить угловую скорости . Кинетический момент создается за счет возбуждения и поддержания стабильными колебания ротора ММГ при помощи специальной системы управления. Физически момент управления создается датчиком момента или электростатическим приводом (5), имеющим форму гребенчатых структур. Часть гребенчатых структур сформирована в теле ротора, а другая закреплена на корпусе таким образом, чтобы зубцы подвижной и неподвижной частей имели взаимную область перекрытия площадей. В этом случае после подачи напряжения на неподвижную гребенку возникает электростатическая сила, стремящаяся затянуть зубцы подвижной гребенки в пазы неподвижной.

Для измерения угла поворота ротора относительно оси Z используются аналогичные гребенчатые структуры, образующие за счет электрической схемы включения датчик угла (2). При повороте ротора относительно оси Z площадь перекрытия зубцов изменяется, соответственно, изменяется и емкость датчика угла, регистрируемая в дальнейшем специальным преобразователем «емкостьнапряжение».

Измерения поворота ротора относительно оси вторичных колебаний Х также осуществляется при помощи датчика емкостного типа (4), неподвижные электроды которого расположены на корпусе, а в качестве общего электрода используется тело ротора. При повороте ротора относительно оси X изменяется зазор между электродами датчика, а следовательно и емкость, что так же как и в канале первичных колебаний, регистрируется с помощью специального преобразователя «емкость  напряжение».

Можно показать, что упрощенная линеаризованная система уравнений движения ротора ММГ, не учитывающая перекрестные связи и вредные моменты, имеет следующий вид [25, 59, с.103]:

; (1.2.27)

, (1.2.28)

где , – углы отклонения ротора ММГ относительно осей первичных Z и вторичных X колебаний; , – показатели затухания колебаний ротора относительно осей Z и X; , – собственные частоты подвеса ротора ММГ относительно осей Z и X; – момент инерции ротора относительно оси X; , – управления, вводимые по осям первичных и вторичных колебаний.

Задачей управления по оси первичных колебаний является возбуждение и стабилизация колебаний ротора с заданной частотой и амплитудой . На практике частота возбуждения первичных колебаний часто совпадает с собственной частотой первичных колебаний ротора , что вызвано необходимостью использования резонансного усиления для достижения заданной амплитуды колебаний. После завершения переходных процессов движение ротора относительно оси Z принимает вид угловых колебаний:

; (1.2.29)

. (1.2.30)

Соответственно выражения для кинетического момента ротора и момента сил Кориолиса принимают вид гармонических и амплитудно-модулированных сигналов:

; (1.2.31)

, (1.2.32)

где – момент инерции ротора относительно оси Z.

С учетом (1.2.32) можно видеть, что уравнение (1.2.28) является нестационарным, поскольку входной сигнал угловой скорости модулируется по величине в соответствии с гармоническим законом с частотой первичных колебаний. Это также означает, что вынужденные колебания ротора по оси вторичных колебаний будут происходить на частоте первичных колебаний, и для выделения полезного сигнала из измеренного сигнала необходимо выполнять процедуру синхронного детектирования.

Также следует иметь в виду, что в общем случае значения моментов инерций , , показателей затухания , и собственных частот , по осям X и Z не равны между собой, что может оказывать существенное влияние на характеристики ММГ.

Вместе с тем нетрудно заметить, что левые части уравнений (1.2.27)(1.2.28), описывающее поведение угла поворота ротора вокруг оси первичных и вторичных колебаний, с точностью до обозначений совпадают с уравнением (1.2.20). Таким образом, собственное движение системы может быть исследовано с использованием полученных в подразделе 1.2.3 функций.

Для анализа движения ротора по оси вторичных колебаний в случае гармонического воздействия, модулированного по амплитуде необходимо привлечение теории анализа систем с амплитудной модуляцией.