Эквивалентная спектральная плотность возмущающего воздействия в частных случаях
“Точечная” цель (
).
В этом случае
и эквивалентная спектральная плотность
возмущающего воздействия определяется
выражением:
Справедливо
как при малых, так и больших отношениях
сигнал/помеха
.
а) для дальномера:
б) для угломеров при линейном сканировании ДН антенны в случае медленно флуктуирующего ОС:
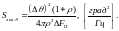
в) для
измерения скорости
(доплеровской частоты) этот случай не
применим, так как при реализации
междупериодного когерентного накопления
.
По крайней мере, это соотношение
целесообразно выдерживать.
2) “Умеренно протяженная” цель .
В этом случае
и
эквивалентная спектральная плотность
возмущающего воздействия определяется
выражением:
Этот случай
характерен для измерения скорости и
дальности для крупноразмерных целей
при высоком разрешении по
.
Например, для измерителя скорости:
Сильный сигнал .
Ошибки оценки координат целей
Ошибка оценки координат или параметра определяется:
флуктуационной ошибкой, обусловленной возмущающим воздействием (наличие шумов, флуктуаций ОС);
динамической ошибкой, обусловленной инерционностью измерителя или устройства оценки координат.
Ошибку оценки
параметра
можно характеризовать среднеквадратическим
значением ошибки, которое в силу
независимости флуктуационной и
динамической ошибок определяется
выражением:
где
и
- соответственно, дисперсии флуктуационной
и динамической ошибок.
Наиболее правильно рассматривать динамическую ошибку как смещение или математическое ожидание ошибки изменения D, а флуктуационную ошибку как случайное состояние. Соответственно, закон распределения ошибки изменения (в установившемся состоянии, то есть когда переходные процессы закончились) имеет вид:
Рассмотрим ошибки
оценки параметра
измерителем за время наблюдения
.
В этом случае флуктуационная ошибка
определяется как произведение
эквивалентной спектральной плотности
возмущающего воздействия на полосу
пропускания устройства оценки
(измерителя):
где
- полоса пропускания устройства оценки.
Динамическая
ошибка устройства оценки обусловлена
изменением среднего значения параметра
за время наблюдения и равна:
где
- математические ожидания скорости и
ускорения изменения параметра
.
Дискриминаторы следящих измерителей радиальной скорости
2.1 Оптимальный дискриминатор
Сигнал ошибки, формируемый на выходе оптимального дискриминатора измерителя скорости, определяется производной от квадрата модуля обобщенного корреляционного интеграла по измеряемому параметру – частоте Доплера:
- ошибка измерения.
Выражение для обобщенного корреляционного интеграла имеет вид:
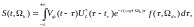
Выражение для алгоритма работы оптимального дискриминатора преобразуется к виду:
Для определения
структуры оптимального дискриминатора,
рассмотрим формирование производной
.
Коррекция по частоте может производиться:
- либо управлением частотой опорного сигнала (как записано в выражении для корреляционного интеграла);
- либо управлением частотой настройки фильтра, осуществляющего междупериодное когерентное накопление.
В последнем случае частоту коррекции необходимо учитывать в импульсной характеристике (ИХ) фильтра:
- комплексная
огибающая ИХ фильтра.
С учетом такой реализации:
В этом случае в
обобщенном корреляционном интеграле
от
зависит только ИХ фильтра
и производную от обобщенного корреляционного
интеграла можно представить в виде:
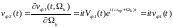- ИХ фильтра,
позволяющего формировать производную
.
Найдем частотную характеристику (ЧХ) НЧ аналога этого фильтра:
- АЧХ НЧ аналога
фильтра, формирующего на выходе
корреляционный интеграл.
Вывод. ЧХ второго фильтра, формирующего в оптимальном дискриминаторе производную от обобщенного корреляционного интеграла, является производной по частоте от ЧХ первого фильтра, формирующего обобщенный корреляционный интеграл.
Пример. Пусть в качестве радиоинтегратора (РИ) коррелятора выступает одиночный колебательный контур, НЧ аналог которого имеет АЧХ:
Следовательно,
второй фильтр представляет собой
последовательно включенные фазовращатель
(ФВ) и два РИ. Постоянная времени
является постоянным множителем, не
влияющим на форму АЧХ второго фильтра.
Эти рассуждения позволяют представить облик оптимального дискриминатора измерителя радиальной скорости:
Рассмотрим работу схемы:
При
сигнал на выходе первого УПФ формируется
на частоте, ниже промежуточной. Такое
колебание во втором УПФ получит
положительный фазовый сдвиг, который
при больших рассогласованиях будет
близким к
.
С учетом ФВ на (
)
разность фаз входных сигналов ФД
(скалярного перемножителя) будет больше
и выходной сигнал ошибки будет
отрицательным
.
При нулевом
рассогласовании (
)
сигнал на выходе первого УПФ будет
формироваться строго на промежуточной
частоте. В этом случае фазовый сдвиг,
вносимый вторым УПФ, будет равен нулю.
Входные сигналы ФД будут ортогональны
(
)
и выходной сигнал ФД будет равен нулю
.
При
второй полосовой фильтр даст отрицательное
смещение фазы выходного сигнала. Поэтому
с учетом ФВ на (
)
разность фаз входных сигналов ФД будет
меньше
и выходной сигнал ФД будет больше нуля
.