26. Методы построения переходных процессов в сау

Наибольшее распространение получили:

1) классический метод (непосредственное решение д.у.)

2) операторный метод

3) метод трапецеидальных ВЧХ(вещественная частотная х-ка)

4) использование ЭВМ

1. Классический

Рассм. лин.д.у., описывающее движ-е САУ. D(p)*y(t)=k(p)U(t)+N(p)f(t) (1)

где p=d/dt D(p),k(p),N(p)-полиномы во времени

y(t)-выходная регулируемая величина; U(t)-управляющее воздействие; f(t)-возмущающее возд. Решение уравнения (1) имеет вид:y(t)= yn(t)+ yb(t);y(t)=полное решение уравнения (1)

yn(t)-общее решение однородного д.у. D(p)y(t)=0. Эту составляющую часто называют переходной yb(t)-возмущающая составляющая или частное решение, которое определяется правой частью ур-ия (1). Как известно общ. Решение уравнения (1) может быть представлено из корней характеристического уравнения D(p)=0

yn(t)=c1ep1t+c2ep2t+…+ cnepnt - для вещественной

yn(t)= (c1+c2t)ep2t –для двукратного вещ. корня

yn(t)=c1e(+j)t+c2e(-j)t=Ai*e1t*sin(It+i); ci,Ai, i – постоянные интегрирования. Полное решение (1) будет иметь вид y(t)=yb(t)+ c1ep1t+c2ep2t+…+ cnepnt (2) для отыскания постоянной интегрирования используем начальные условия t=0;y(0)=y0;y|(0)=y|0;

y(n-1)(0)=y0(n-1) дифференцируем уравнение (2) (n-1) раз и используем н.у. получаем систему из n алгебраических уравнений, с n неизвестными, c1, c2, c3,…, cn, от куда и определ-я пост. интегрирования.

2. Операторный

Он основан на интегральном преобразовании Лапласа. В изображ. решен. диф. ур-я имеет вид: Y(p)=W(p)*U(p), и выполнив преобразование Лапласа получим оригинал т.е решение ур-я при нулевых начал. условиях.y(t)=L-1{W(p)*U(p)}, различ. след. способы нахождения оригинала: 1) табличный, 2) по теореме разложения, 3) по теореме свертывания. Для определ. интеграла можно использовать теорему разложения. Например для случая разных веществ. корней хар-го ур-я: p1, p2, p3,…, pn, можем записать Y(p)= bmpm+…+b1p+ b0/ anpn+…+a1p+a0=K(p)/ an(p-p1)(p-p2)… (p-pn) тогда решене исход. Ур-я динамики можно будет записать: y(t)= Σni=1 (K(pi)/D’(pi))*epit, D’(pi)=dD(p)/dp при p= pi, где pi- корни хар-го ур-я D(P)=0. Аналогичные ф-лы есть для случая кратных и комплексных корней. Теорема свертывания гласит если изобр. решения диф. ур-я представл. собой производные двух ф-ий для которых известны оригиналы L-1 {W(p)}=ω(t), L-1 {U(p)}=u(t), то ориг. Решения y(t) может быть вычислен с помощью интеграла свертки или интеграла Дюамеля. y(t)=∫t0W(τ)* U(t-τ)dτ. Интеграл Дюамеля связывает мгновенные значения вых и вх сигналов с учётом влияния предысторий. Функция w() отражает с которым предыдущее значение n(t-) участвует в формировании выходного сигнала.

Достоинства:

1) операторные методы используют алгебраические выражения

2) постоянные интегрирования вычисляются автоматически из нулевых начальных условий

3) метод ориентирован на табличное решение

Недостатки:

1)необходимость нахождения корней

3. Метод трапецеидальных вчх

П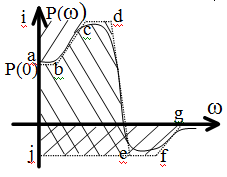 оследов. расчетов:

1-й шаг: представл. график ВЧХ в виде горизонт. и наклонных линий.

2-й шаг: из этих отрезков составл. трапеции, которые одной примыкают к оси ординат.

3-й шаг: перемещаем трапеции чтобы их основания оказались на оси абцисс.

Ч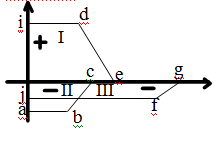 тобы сумма площадей трапеции приближалась к площади под кривой ВЧХ, площадь I берем со знаком “+”, II-III cо знаком “-“.

P(ω)= Σni=1Pi(ω)- трапецеид. ВЧХ. H(t)= 2/П

)= наибольшая погрешность апраксимации лежит в области высоких частот. Отброшенный высокочастотный хвост ВЧХ отразиться только на начальном участке перех-ой хар-ки. (ω→ , t→0) =Σhi(t).

4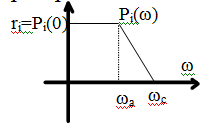 -й шаг: для каждой трапеции находим составл-ю перех. хар-ки. Для этого использ. таблицу так назыв. h-функций: hi(t). Сначала опред.

Параметры трапеции

а) ri=Pi(0)- высота трапеции,

б) χi=ωai/ωci- коэф. наклона в интер-ле (0;1). Таблицы составл. для единичной трапеции Pi(0)=1 и для различных

коэфф. наклона χi=0;0.05;…;0.95;1. Таблицы составл. для безразмерного времени τ=ωc(t). Из таблицы извлекаем значение перех-ой хар-ки. h1i(t)- еден. трапеция. Затем коорд. Времени: ti= ri/ωci, hi(t)=ri*h1i(t).

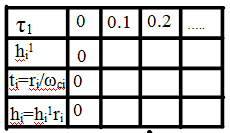
Повторяя вычисл. для других трапеций находим все составл-е hi. строим график hi с учетом знаков трапеции и графически

суммируем.

Источник:

• шпоры которые с интернета