22.Запас устойчивости по максимуму ачх замкнутой системы. М-окружности и их свойства.

В соответствии с критерием устойчивости Найквиста мерой запаса устойчивости можно считать степень удаления точек годографа КЧХ разомкнутой системы от точки -1,j0, которая может быть определена по величине максимума АЧХ замкнутой системы.

Д опустим, что КЧХ разомкнутой системы W_р.с(jω) располагается на комплексной плоскости, как показано на рис.4.12. Тогда АЧХ замкнутой системы А_з.с(jω) определится через W_р.с(jω) с помощью соотношения

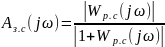
Числитель для некоторой частоты ω_i равен длине отрезка ОА, а знаменатель – длине отрезка ВА. Отсюда

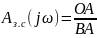
При нулевой частоте значение КЧХ достаточно велико, поэтому соотношение отрезков близко или равно единице. С ростом частоты точка А движется в направлении стрелки и в пределе, при 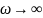длина вектора ОА стремится к нулю. А вектора ВА к единице; соответственно модуль характеристики тоже стремится к нулю.

Однако характер изменения соотношения при 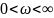различен в зависимости от степени удаления характеристики W_р.с(jω) от точки -1,j0 (точки В на рис.4.12).

Если КЧХ располагается достаточно далеко, то длина вектора ВА остается всегда больше длины вектора ОА и их соотношение монотонно уменьшается от значения при 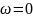до нуля при .

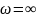Если же КЧХ располагается близко, то вначале соотношение отрезков с ростом частоты возрастает, поскольку длина ОА уменьшается медленнее, чем уменьшается длина ВА. Достигнув максимального значения при некоторой частоте ω_рез, это соотношение затем стремится к нулю.

В предельном случае, когда КЧХ проходит через точку -1,j0 (система на границе устойчивости), длина вектора ВА становится равной нулю, а значение максимума АЧХ бесконечно большим.

Относительное значение резонансного пика АЧХ замкнутой системы в виде 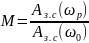принято называть частотным показателем колебательности.

Найдем геометрическое место точек в плоскости характеристики W_р.с(jω), которое удовлетворяет условию постоянства соотношения длин векторов . Из рис.4.12 следует:

, .

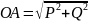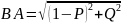т.е.

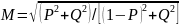
После преобразований получим:

Это уравнение окружности радиуса 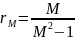, с центром на отрицательной вещественно полуоси на расстоянии 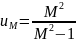от начала координат.

Семейство таких окружностей показано на рис.4.13. Очевидно, что индекс окружности М, которую пересекает характеристика W_р.с(jω) при частоте ω₁, равен значению АЧХ замкнутой системы при этой частоте. Индекс о кружности, которой характеристика только касается, не пересекая ее, равен максимуму АЧХ (при ) .

Сабанин с126-127

Ротач с121-124

23.Расчет аср с п-, и- и пи–алгоритмами регулирования на заданный запас устойчивости по «m» и «m».

При ограничении на запас устойчивости по корневому показателю колебательности m, условием требуемого запаса устойчивости для системы с ПИ-регулятором будет:

Переписав это уравнение в виде двух уравнений для вещественной и мнимой части, получим:

Для И-регуля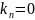тора , для П-регулятора .

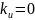При ограничении на запас устойчивости по частотному показателю колебательности m

Ротач с139,146

24. Прямые и косвенные критерии качества процессов регулирования, ориентированные на ступенчатое возмущающее действие

Прямые критерии:

1.Величина максимального отклонения регулируемой величины y_дин( динамическая ошибка или первый выброс)

2.Величина остаточного установившегося отклонения y_уст после окончания переходного процесса или сумма y_дин+ y_уст

3.время регулирования t_рег ( длительность процесса), т.е время в течение которого отклонение достигает какой-то наперед заданной величины ±Δ и в дальнейшем ее не превышает

4.колебательность процесса

Качество процесса тем выше, чем меньше эти показатели

Качество процесса считается тем выше, чем меньше показатели y_дин и t_рег , при условии достаточно большого запаса устойчивости системы, определяемого либо должным расположением корней характеристического уравнения системы, либо должным видом частотных характеристик замкнутого контура системы [Ротач]

Используется ступенчатое возмущение, т. к является наиболее тяжелым для систем регулирования!

Т.к. прямые критерии качества регулирования нельзя связать с параметрами настройки регулятора вводятся косвенные интегральные критерии

1.Линейный интегральный критерий и его свойства.

.

«+»Инвариантен по отношению к точке приложения возмущения.

Простота расчетов ( нет необходимости знать матем. модель)

«-» искажает показатели при отрицательных отклонениях, применяется для слабоколебательной системы

В АСР с И-,ПИ-,ПИД-рег-ми значение 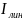опред-ся значением коэф-та при интегральной составляющей =1/kи. Минимуму отвечает kи→max, k_п./T_и→max

2.Квадратичный интегральный критерий и его свойства.

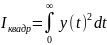.(возведение в квадрат- для устранения влияния отрицательных значений)

-не инвариантен по отношению к точке приложения возмущения (т.е параметры настройки для мин действия одного возмущения могут не мин другое возмущение)

-Вычисления производится по модулю КЧХ системы.

3.Модульный:

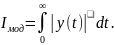
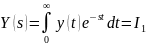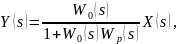,где где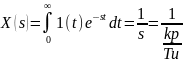

Минимальное значение 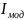при макс значении Ки=Кр/Ти

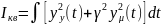
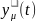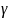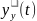Иногда ограничение на запас устойчивости вводится функцией штрафа, такие инт. Критерии являются обобщенными -переходная хар-ка отн. регулирующего воздействия - коэффициент веса функ. Штрафа - отн. управляющего воздействия