
- •1. Предмет тер вера. Случ опыт. Случ событие.Элемент событие. Мн-во эл событий
- •2.Достоверн и невозможн событие. Сумма, разность, произведение.
- •3. Несовместные события. Полная группа событий. Противоположные события.
- •4. Классич и статистич определение вероятностей.
- •5. Формулы комбинаторики
- •6. Вероятн суммы несовместных событий. Следствия (о вероятн против события и суммы вер группы событий)
- •7.Теорема сложения вер 2х совместных соб. Вер суммы неск совместн событий как вер появления хоты бы одно из неск событий.
- •8. Условная вероятнось. Завис и независ события. Теорема умножения вероятней ( для 2х событий)
- •9. Формула полной вероятности
- •10. Формула Байеса (учебник)
- •10. Формула Байеса (лекции)
- •11. Схема Бернулли. Теорема Бернулли. Теорема Пуассона.
- •12. Случайные величины. Дискретные и непрерывные случайные величины
- •13. Закон распределения дискретной случайной величины
- •14. Функция распределения дискретной случайной величины
- •2. Свойство:
- •15. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
- •16. Дисперсия дискретной случайной величины. Св-ва дисперсии. Среднее квадратическое отклонение.
- •18. Закон распределения Пуассона. Математическое ожидание и дисперсия дискретной случайной величины, распределенной по закону Пуассона.
- •19.Функция распределения вероятностей непрерывной случайной величины и ее свойства.
- •20. Плотность распределения вероятностей непрерывной случайной величины и ее свойства.
- •21. Математическое ожидание и дисперсия непрерывной случайной величины. Среднее квадратическое отклонение.
- •22. Мода. Медиана. Наивероятнейшее число появления события в независимых испытания Бернулли. Геометрическая интерпретация числовых характеристик случайных величин.
- •24. Экспоненциальное распределение: плотность, функция распределения, математическое ожидание и дисперсия.
- •25. Нормальное распределение: плотность, функция распределения, математическое ожидание и дисперсия. Стандартное нормальное распределение. Функция Лапласа. Интеграл Пуассона.
- •27. Многомерные случайные величины. Закон распределения двумерной случайной величины. Закон распределения составляющих.
- •Условные законы распределения:
- •Функции регрессии:
- •Плотность распределения составляющих двумерной дискретной случайной величины.
- •Зависимые и независимые случайные величины.
- •Линейная зависимость между случайными величинами и значение коэффициента корреляции:
- •35. Центральная предельная теорема – теорема Ляпунова
- •Локальная теорема Лапласа:
- •33. Закон больших чисел.
- •34. Теорема Бернулли
12. Случайные величины. Дискретные и непрерывные случайные величины
Величина называется случайной, если в результате опыта она не может принимать любые заранее неизвестные значения, т.е. это функция, определенная на множестве событий.
Случайные величины делятся на дискретные и непрерывные.
Величина называется дискретной, если она может принимать определенные, фиксированные значения в области целых чисел. Например, число ежедневно продаваемых в магазине холодильников является дискретной случайной величиной.
Множество значений случайных величин:
 R1
Дискретная
случайная величина
R1
Дискретная
случайная величина
-2 0 2
Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга. Примером непрерывной случайной величины является время заправки автомашины на автозаправочной станции.
 R1
Непрерывная
случайная величина
R1
Непрерывная
случайная величина
p а b
Случайная величина обычно обозначается прописной буквой латинского алфавита (Х,Y), её конкретные значения – строчными буквами (х,у). Для дискретных случайных величин при решении конкретных задач указываются их возможные числовые значения. Например, х1=3, х2=1, х3=5
13. Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют перечень её возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, первая строка которой содержит возможные значения xi , а вторая – вероятности рi:
Х |
х1 |
х2 |
… |
хn |
р |
р1 |
р2 |
… |
рn |
Где
![]()
Если множество возможных значений Х бесконечно (счетно), то ряд р1+р2+…сходится и его сумма равна единице.
Закон распределения
дискретной случайной величины Х может
быть задан также аналитически (в виде
формулы):
![]() или с помощью функции распределения:
F(x)=Р(Х<х)
или с помощью функции распределения:
F(x)=Р(Х<х)
Закон распределения
дискретной случайной величины можно
изобразить графически, для чего в
прямоугольной системе координат строят
точки
![]() и соединяют их отрезками. Полученную
фигуру называют многоугольником
распределения.
и соединяют их отрезками. Полученную
фигуру называют многоугольником
распределения.
рi
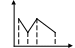 хi
хi
14. Функция распределения дискретной случайной величины
Пусть дискретная случайная величина Х может принимать n значений х1, х2, …, хn . Для полной характеристики этой случайной величины должны быть заданы ещё и вероятности появления указанных значений р1, р2,…., рn . Дискретные значения случайной величины и вероятности их появления удобно записывать в следующем виде:
Х |
х1 |
х2 |
… |
хn |
р |
р1 |
р2 |
… |
рn |
Для дискретной случайной величины, так же как и для непрерывной, вводится понятие функция распределения, которая представляет собой вероятность события X<x, где х – задаваемые непрерывно изменяющиеся значения, т.е. F(x)=Р(Х<х)
Если дискретные значения случайной величины х1,х2,…хn располагались в порядке возрастания, то каждому значению хi этих величин ставится в соответствие сумма вероятностей всех предыдущих значений и вероятности рi:
х1 |
х2 |
х3 |
… |
р1 |
р1+р2 |
р1+р2+р3 |
… |
Так как до значения
x1
случайная
величина Х не встречалась, то и вероятность
события Х<х1
равна 0. Для
всех значений
![]() вероятность события Х<х
совпадает
с вероятностью значения x1,
т.е. р1.
Но при х>x2
случайная
величина уже может принимать два
возможных значения х1
и х2,
поэтому вероятность события Х<х для
вероятность события Х<х
совпадает
с вероятностью значения x1,
т.е. р1.
Но при х>x2
случайная
величина уже может принимать два
возможных значения х1
и х2,
поэтому вероятность события Х<х для
![]() будет
равна сумме вероятностей р1
и р2 и
тд Нанося на график возможные дискретные
значения случайной величины х и
соответствующие суммы вероятностей,
получаем ступенчатую форму, которая и
является графиком функции распределения
вероятностей
будет
равна сумме вероятностей р1
и р2 и
тд Нанося на график возможные дискретные
значения случайной величины х и
соответствующие суммы вероятностей,
получаем ступенчатую форму, которая и
является графиком функции распределения
вероятностей
F(x)
p1
p1
+ p2
p1
+ p2
+ p3
1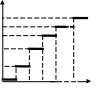 Х
Х
0 X1 X2 X3 X4 Хn
Часть вместо термина «функция распределения» используют термин «интегральная функция распределения»
Св-ва функции распределения:
1 Свойство: F(x) является неубывающей:
Док-во:
![]()
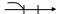 Х
Х
х1 х2
![]()
![]()
![]()
![]()
Следствия из 1ого св-ва
1.1.![]()
1.2. Р(X=x1 )=0
