Экзаменационный билет № 12

1. Реальные газы. Силы Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и Эндрюса. Метастабильные состояния: пересыщенный пар и перегретая жидкость. Критическое состояние, критические параметры. Равновесие жидкости и насыщенного пара. Уравнение Клапейрона-Клаузиуса. Внутренняя энергия реального газа. Эффект Джоуля-Томсона.

2. Микроканоническое и каноническое распределения Гиббса. Статистический интеграл системы. Энтропия. Большое каноническое распределение (классический и квантовый случай). Термодинамическая эквивалентность канонических распределений.

1 . Реальные газы. Силы Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и Эндрюса. Метастабильные состояния: пересыщенный пар и перегретая жидкость. Критическое состояние, критические параметры. Равновесие жидкости и насыщенного пара. Уравнение Клапейрона-Клаузиуса. Внутренняя энергия реального газа. Эффект Джоуля-Томсона.

Для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона-Менделеева (pV=RT) не пригодны. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

Собственный объем молекул. Силы отталкивания противодействующие проникновению в занятый молекулой объем других молекул, сводится х тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V_m, a V_m-b , где b — объем, занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул

Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого — внутренним давлением. По вычислени­ям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату моляр­ного объема, т. е. Р' = а/V_m² ,где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного при­тяжения, V_m — молярный объем.

Вводя эти поправки, получим уравнение Вав-дер-Ваальса для моля газа (уравнение состояния реальных газов): (Р+ а/V_m² ) (V_m-b) = RT. Для произвольного количества вещества  газа уравнение Ван-дер-Ваальса примет вид (Р+ ²а/V² ) (V-b) = RT, где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем.

Изотермы Ван-дер-Ваальса и их анализ. Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса.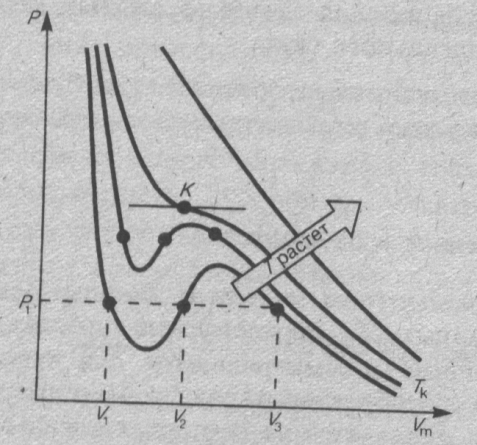

При высоких температурах (Т > Т_кр) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кри­вой. При некоторой температуре Т_кр на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура Т_кр — крити­ческой температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем и давление называются также критическими. Состояние с критическими парамет­рами называется критическим состоянием. При низких температурах (Т < Т_кр) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

Р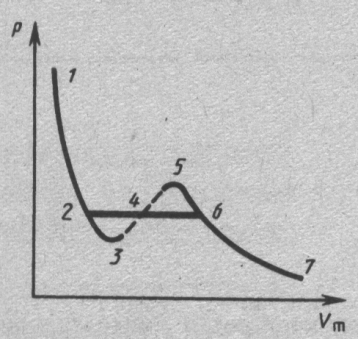 ассматривая различные участки изотермы при Т<Т_кр, видим, что на участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообраз­ное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—I (изотерма Эндрюса). Часть 6—7 отвечает газообраз­ному состоянию, а часть 2—/ — жидкому. В состояниях, соответствующих горизон­тальному участку изотермы б—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Д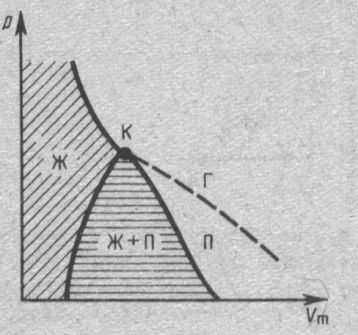 ля нахождения критических параметров подставим их значения в уравнение Ван-дер-Ваальса : р_кр V³ –(RT_кр+p_крb)V²+aV-ab=0 Поскольку в критической точке все три корня совпадают и равны , уравнение приводится к виду р_кр(V-V_кр)³=0 В этих уравнениях должны быть равны и коэф­фициенты при неизвестных соответствующих степеней. Поэтому можно записать три уравнения, решая полученные уравнения, найдем

V_кр=3b, p_кр=а/(27b²) , T_кр=8a/(27Rb)

Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая, ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р, Vm под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.

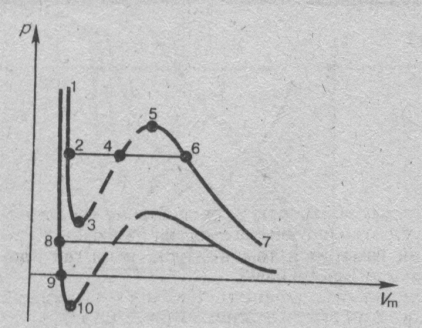
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. справа), видим, что последняя имеет прямолинейный участок 2—б, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть ре­ализованы состояния, изображаемые участками Ван-дер-Ваальсовой изотермы 5—6. и 2—3. Эти неустойчивые состояния называются метастабильными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенньн пар. Обе фазы ограниченно устойчивы.

При достаточно низких температурах изотерма пересекает ось V_m, переходя в область отрицательных давлений (нижняя кривая). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9—10 — растянутой жидкости.

Д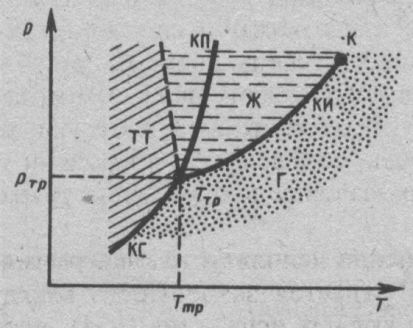 ля наглядности фазовых превращений используется диаграмма состояний, где КИ, КП, КС-кривые испарения, плавления, сублимации; ТТ –твердое тело.

Термодинамика дает метод расчета равновесия двух фаз – уравнение Клапейрона-Клаузиуса: dр/dT=L/(T(V₂-V₁)), где L-теплота фазового перехода, (V₂-V₁)-изменение объема вещества при переходе. Оно позволяет определить наклоны кривых равновесия.

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (определяет внутреннюю энергию идеального газа, равную СvТ) и потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, как известно из механики, идет на увеличение потенциальной энергии системы, т. е. A=p'dV=П, или П =-(а/V²)dV Знак минус означает, что молекулярные силы, создающие внутреннее давление р', являются силами притяжения . Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа U= СvТ –a/V растет с повышением температуры и увеличением объема. Можно доказать, что при адиабатическом расширении без совершения внешней работы внутренняя энергия не меняется (1 начало термодинамики.), но температура уменьшается, так как совершается работа против сил притяжения.

Эффект Джоуля-Томсона – адиабатическое расширение реального газа с совершением внешими силами положительной работы. Из 1 начало термодинамики U+pV=const.- неизменная величина (энтальпия), подставив в неё всё приведенное выше получим: Т₂-Т₁=(2а(1/V₂-1/V₁)-b(p₂-p₁) -ab(1/V₂²-1/V₁²)) /(Cv+R), то есть знак разности температур зависит от величины поправок (при а=0 без сил притяжения, газ нагревается; при b=0 - охлаждается) и от значений начальных объема и температуры. Эффект Джоуля-Ленца положительный – при охлаждении, отрицательный – при нагревании. Температура, при которой происходит изменение знака эффекта – температура инверсии. Т=(2a/Rb)(1-b/V), - кривая инверсии. (ниже кривой положительный эффект).

2. . Микроканоническое и каноническое распределения Гиббса. Статистический интеграл системы. Энтропия. Большое каноническое распределение (классический и квантовый случай). Термодинамическая эквивалентность канонических распределений.

Рассмотрим многочастичную термодинамически равновесную систему. Основная идея статфизики сос­тоит в замене среднего по времени (b(q, р)); функции b(q, p)

данной системы средним значением b(q, p) этой функции по ан­самблю определенным образом распределенных систем где фазовая плотность распределения p(q, p) для равновесных систем, очевидно, не зависит от времени и удовлетворяет условию нормировки Задача состоит в том, чтобы найти p(q, p), удовлетворяющую равенству Для этого обратимся прежде всего к основному уравнению ста­тистической физики классических систем — уравнению Лнувилля. Из него получаем откуда следует, что равновесная функция распределения p(q, p) является интегралом движения уравнений Гамильтона или функцией интегралов движения: В соответствии с введенным Гиббсом (отвечающим термодина­мике) статистическим определением энтропии (см. ниже) функция p(q, p) зависит лишь от однозначных аддитивных интегралов дви­жения. Известны три таких интеграла движения: энергия Н, им­пульс Р и момент импульса М. Поэтому Для равновесной системы частиц в неподвижном сосуде им­пульс Р и момент импульса М равны нулю. Поэтому в этом слу­чае для систем с заданным числом частиц фазовая плотность рас­пределения зависит лишь от функции Гамильтона Для определения явного вида функции распределения в статис­тической физике принимается в качестве основного положения по­стулат равной априорной вероятности любого микросостояния равновесной изолированной системы, т. е. принимается, что для изолированной системы, имеющей энергию Е с точностью (определяемой заданием макроскопических условий) и число частиц N в объеме V, функция распределения p(q, p) постоянна в слое и равна нулю вне этого слоя:

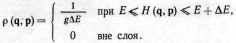Равновероятностное распределение микросостояний изолиро­ванной системы называется микроканоническим распределением, а соответствующий ансамбль — микроканоническим ансамблем. С помощью б-функции микроканоническое распределение (12.9) можно записать в виде

П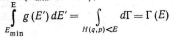 остоянная g(E, N, V) определяется из условия нормировки и имеет смысл плотности распределения фазового объема по энер­гии. Действительно, интеграл от g(E') по допустимым значениям энергии, меньшим Е (Еmin<E'<Е), равен фазовому объему (приведенному), заключенному внутри гиперповерхности Н(q, р) =Е. Увеличение фазового объема Г(Е) при возрастании энергии на величину Е называется статистичес­ким весом макроскопического состояния системы с энергией E и равно где g(E) — энергетическая плотность фазового объ­ема, или, поскольку точки фазового объема изображают состояния, плотность состояний системы с данной энергией Е. Можно показать, что микроканоническое распределение обеспечивает равенство среднего по макроканоническому ансамблю среднему по времени функции координат к импульсов систем. Такие системы называются эргодическими. Обоснование (исходя из механики) эргодичности многочастичных систем и возможности замены средних по времени средними по микроканоническому ансамблю носит название эргодической проблемы. Эта проблема несмотря на ряд полученных важных результатов еще ждет своего решения. Для построения термодинамики многочастичной системы дос­таточно, как известно, определить один из ее термодинамических потенциалов. Остальные величины находятся уже методами самой термодинамики. При независимых макроскопических параметрах E, V, N, которыми определяется термодинамическое состояние рассматриваемой системы, термодинамическим потенциалом явля­ется энтропия. Гиббс определяет ее как величину, пропорциональ­ную логарифму фазового объема где k — универсальная постоянная, равная постоянной Больцмана. Можно показать, что определенная таким образом энтропия обладает известными термодинамическими свойствами.

Заметим, что поскольку при определении энтропии в статис­тическом пределе (N=>, V=>, V/N = v = const) следует учиты­вать только основную асимптотику по числу частиц —N, то опре­деление статистической энтропии не является единствен­ным. Так, например, можно использовать вместо эквива­лентные выражения в виде логарифмов или плотности состояний i статистического веса Логарифмический вид выражений для энтропии обусловлен требованием ее аддитивности, в частности, для невза­имодействующих подсистем. Вычисление фазового объема или ста­тистического веса даже для относительно простых статистических систем .представляют трудную задачу. Поэтому микроканоничес­кое распределение используется в основном не для вычисления термодинамических функций конкретных систем, а для общетеоре­тического рассмотрения. Каноническое распределение Найдем распределение по состояниям (функцию распределения в фазовом пространстве) неизолированной (но замкнутой) систе­мы, находящейся в тепловом контакте с другой системой значи­тельно больших размеров (по числу степеней свободы) — термо­статом. Т — температура термостата и системы, находим каноническое распределение Гиббса

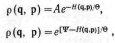
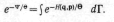
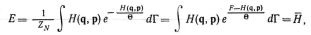где  — kT называется модулем канонического распределения, а константа A содержит все не зависящие от q и р вели­чины и определяется из условия нормировки Входящий интеграл 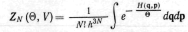называется статистич. интегралом системы, а определяемая есть ее энергия Гельмгольца F(T,V,N). Действительно, вычислим внутренние уравнению Гиббса—Гельмгольца т. е. что внутренняя энергия статистической системы равна сред­нему значению ее функции Гамильтона по каноническому распре­делению Гиббса как и должно быть в соответствии с фи­зическим смыслом Е. 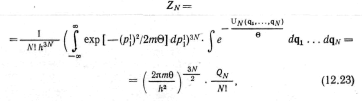Поскольку функция Гамильтона системы равна сумме кинетической и потенциальной энергий ее частиц, а кинетическая энергия есть квадратичная функция импульсов, то интегрирова­ние по ним в может быть произведено и мы получим называется конфигурационным интегралом. Интегрирование по импульсам канонического распределения Гиббса легко выполняется и дает конфигурационное рас­пределение Гиббса 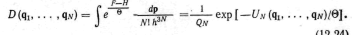Энергия Гельмгольца — тепловая длина волны де Бройля. Таким образом вычисление энергии Гельмгольца, а следова­тельно, и всех термодинамических функций многочастичной си­стемы сводится к вычислению ее конфигурационного интеграла (12.24). С помощью известных термодинамических соотношений (5.17) 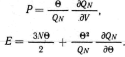С помощью канонического распределения находим, что энтропия

с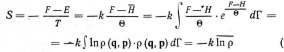 истемы пропорциональна среднему значению логарифма плотности веро­ятности, а не является

средним значением какой-либо механиче­ской величины. Большое каноническое распределение Определим теперь распределение по состояниям открытой си­стемы в термостате, называемое большим каноническим распре­делением Гиббса. С такими системами мы встречаемся в целом ряде приложений. Кроме того, использование большого канони­ческого распределения во многих случаях оказывается более эф­фективным, чем микроканонического и канонического распреде­лений. Рассмотрим малую систему, которая находится в тепловом и материальном контакте с термостатом, обмениваясь с ним не только энергией, но и частицами. Границы, отделяющие систему от термостата в некотором смысле условны: они фиксируют лишь ее объем V и другие внешние параметры а, но не энергию Е и число частиц N. В соответствии с этим термодинамическое со­стояние системы определяется переменными Т, V, N. Большое каноническое распределение получим аналогично выводу канонического, исходя из микроканонического распреде­ления для изолированной объединенной (термостат и изучаемая малая система) системы с энергией ЕО и числом частиц NO. От­личие в рассматриваемом случае системы состоит в том, что те­перь следует в явном виде указывать число частиц в ней. Таким образом, подобно функция распределения си­стемы с переменным числом частиц в термостате имеет вид: 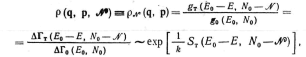где индексы о к т относятся соответственно к объединенной си­стеме и к термостату. 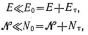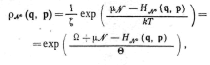Поскольку мы будем предполагать, что для энергии E и числа частиц N подсистемы справедливы нера­венства то в первом приближении где учтено, что Подставляя (12.45) в (12.44), находим распределение Гиббса большое каноническое 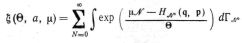большой статистический интеграл (сумма), большой термодинамический потенциал. Действительно, термодинамические параметры —число частиц и внутренняя энергия —определяемые со­ответствующими частными производными большого термодина­мического потенциала, совпадают со средними значениями числа частиц и функции Гамильтона по большому каноническому рас­пределению Г иббса (12.46).

Термодинамическая эквивалентность канонических распределений Мы рассмотрели три гиббсовских распределения: микрокано­ническое — для изолированных систем, каноническое — для не­изолированных закрытых систем в термостате и большое канони­ческое—для неизолированных открытых систем в термостате.За исключением немногих случаев, использование этих распределений для каждой из названных систем приводит в статистическом преде­ле (N=>, V=>, V/N = u = const) к термодинамически эквива­лентным результатам. Это означает, что каноническим и большим каноническим распределениями можно пользоваться также для описания изолированных систем, что практически является очень важным. Во всех практически важных случаях относительная' флуктуация энергии очень мала и в статистиче­ском пределе стремится к нулю. Малость величины относитель­ной флуктуации означает, что зна­чения энергии системы в термоста­те сколько-нибудь отличные от средней энергии, рактически не­вероятны.

Энергии, заметно отличающиеся от Н, чрезвычайно маловероят­ны, и система ведет себя практически как изолированная. Это и приводит к термодинамической эквивалентности результатов, по­лученных с помощью канонического и микроканонического рас­пределений. Аналогично с помощью большого канонического распределе­ния находим: относительная флуктуация числа частиц в системах большого канонического ансамбля

стремится к нулю в статистическом пределе. Отсюда следует эк­вивалентность большого канонического и канонического распре­делений. Заметим, что, несмотря на термодинамическую эквива­лентность статистических ансамблей, расчеты величины флуктуа­ции, проведенные с их помощью, приводят к различным резуль­татам. Как видно из формулы, относительная флуктуация энергии системы в термостате не будет малой тогда, когда бесконечно большая теплоемкость, и аналогично относительная флуктуация не будет малой при нулевая величина коэффициента устойчивости. Это имеет место, как известно из термодинамики, в критическом состоянии и в двухфазных системах. В этих слу­чаях канонические ансамбли не эквивалентны. основы КВАНТОВОЙ СТАТИСТИКИ Квантовые микроканоническое и каноническое распределения. Определение микроканонического и канонического распреде­лений квантовых систем в целом аналогично рассмотренному классическому случаю. Роль функции распределения играет те­перь статистический оператор р или набор коэффициентов wk. определяющих вероятностное распределение по чистым состоя­ниям.

Как следует из уравнения Неймана, равновесный ста­тистический оператор коммутирует с гамильтонианом И для покоящейся системы является его функцией. Поэтому необходимо задать зависимость коэффициентов wk от энергии Ek.

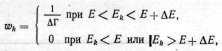
Если число квантовых состояний изолированной системы, имеющей энергию Е с определенным отклонением Е<Е, равно Г(E), то в соответствии с постулатом равной априорной вероят­ности состояний таких систем имеем квантовое микроканониче­ское распределение 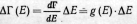из условия нормировки (13.1): 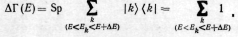а полное число состояний равно 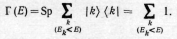Энтропия квантовой статистической системы определяется фор­мулами, 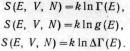Отсюда получаем квантовое канониче­ское распределение по состояниям 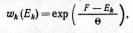или после нормировки 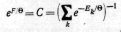называется статистической суммой, а есть энергия Гельмгольца квантовой системы, в чем легко убе­диться. Заметим, что каноническое распределение определяет также распределение по энергиям для системы с невырожденными уровнями энергии. При наличии вырождения, когда одному и тому же энергетическому уровню Е соответствует gt различных состояний, вероятность такого вырожденного зна­чения энергии равна 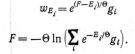Зная энергию Гельмгольца, как функцию своих есте­ственных переменных, все другие термодинамические параметры можно найти методами термодинамики. Энтропия системы равна 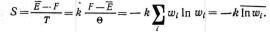Таким образом, исследование квантовой статистической системы с помощью канонического распределения сводится к следующей процедуре:

а) вначале решается динамическая задача по определению энергетического спектра Е; и соответствующего набора кванто­вых чисел i путем решения уравнения Шредингера;

б) потом рассчитывается статистическая сумма (13.11) систе­мы и ее энергия Гельмгольца F(Q, V, N) (13.12);в) и далее вычисляются термодинамические характеристики системы. Квантовое большое каноническое распределение. Рассмотрим свойства открытых квантовых систем в термо­стате. Макроскопически такие системы описываются переменны­ми Т, V, N. Границы, отделяющие систему от термостата, прони­цаемы для частиц. Соответствующее этим условиям распределе­ние по состояниям — большое каноническое распределение — мо­жет быть получено подобно каноническому, исходя из микрока­нонического распределения для объединенной изолированной си­стемы с энергией E0 и числом частиц N0. При этом в дополнение к неравенству для энергии системы необходимо добавить неравенство для числа ее ча­стиц Отсюда, используя микроканоннческое распределение для объ­единенной системы, находим большое каноническое распределе­ние по состояниям i квантовой открытой системы а термо­стате:

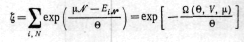
большой термодинамический потенциал. Действительно, вычисленные с помощью (13.19) по формулам термодинамики энергия и число частиц системы равны соответ­ствующим средним по большому каноническому распределению: 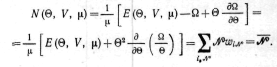Энтропия системы, как и в случае канонического распределения определяется средним значением логарифма функции распреде­ления: 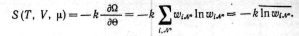Таким образом, при использовании большого канонического распределения для исследования квантовых статистических систем необходимо прежде всего определить энергетический спектр системы из решения уравнения Шредингера Причем в отличие от канонического распределения требуется най­ти зависимость спектра для произвольного числа частиц N, в том числе и для малых N~ 1. Затем следует расчет большой статистической суммы и большого термодинамического потенциала . Далее методами термодинамики вычисляются все необходимые термодинамические характеристики системы.