3.5. Основные положения квантовой механики.

Корпускулярно-волновой дуа­лизм света. Т.о., в одних опытах (дифракция, интерференция, поляризация) свет проявляет волновые свойства, в других же (тепловое излучение, фотоэффект, эффект Комптона) он ведет себя как поток частиц-фотонов, но никогда не проявляет волновые и корпускулярные свойства одновременно. Волновая и квантовая теории света допол­няют друг друга. Двойственная природа света получила название корпускулярно-волнового дуа­лизма света и находит свое выражение в формулах, определяю­щих основные характеристики фотонов. Как видно из этих формул, корпускулярные характеристики фотона – энергия ε_f = hv и импульс р_f = hv/c=h/λ – связаны с волновыми характеристиками света : его частотой ν и длиной волны λ.

Б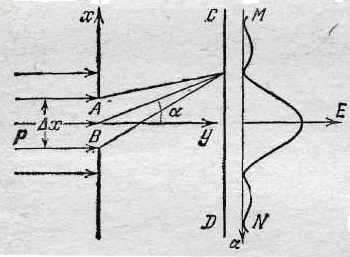 оль­шая группа оптических явлений – интерференция, дифракция, поляризация – полностью объясняется в волновой оптике. Однако, если «перемещаться» от длинных волн в сторону более коротких, то вол­новые свойства света будут проявляться все слабее, уступая место более отчетливо проявляющимся квантовым свойствам. Это видно, например, из существования «красной границы» фотоэффекта и такой же границы для фотохимических реакций.

Рассмотрим связь волновых и квантовых свойств света на примере прохождения света через щель в непрозрачном экране (рис.). Предположим, что параллель­ный пучок монохроматических световых лучей проходит через щель АВ вдоль оси ординат. На экране CD, распо­ложенном за щелью, возникает дифракционная картина. В каждую точку экрана х попадает плоская гармоническая волна : E(x,t)=E₀·exp(-i·k·x) · exp(-i·ω·t)= E(x) · exp(-i·ω·t) и наблюдается определенная освещенность, пропор­циональная интенсивности I(x) в этой точке. На рис. справа изображено распределение интенсивности света по экрану, пропорциональное квадрату амплитуды Е(х) световой волны I(x)~E(x) ².

С квантовой точки зрения образование на эк­ране дифракционной картины означает, что при прохождении све­та через щель происходит перераспределение фотонов в пространстве. В результате этого в разные точки экрана попадает различное число фотонов. Освещенность экрана в данной точке будет тем больше, чем большей будет суммарная энергия фотонов, попадающих за еди­ницу времени в данную точку. Эта энергия, в свою очередь, пропорциональна числу п(x) фотонов, доставивших эту энергию. Таким образом, I(x) ~п(x).

Из сказанного следует, что E(x) ²~п(x). Квадрат амплитуды световой волны в какой-либо точке пространства пропорционален числу фотонов, попадающих в эту точку. Иными словами, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в эту точку. Таким образом, волновые и квантовые свойства света не исключают, а, наоборот, взаимно дополняют друг друга. Квантовые свойства света обусловлены тем, что энергия, импульс и масса излучения сосредоточены в частицах – фотонах. Вероятность нахождения фотонов в различных точках пространства опре­деляется волновыми свойствами света – амплитудой световой волны (квадратом ее модуля).

Далее было установлено, что волновые свойства присущи не только совокупности большого числа одновременно летящих фотонов. Каждый отдельный фотон обладает волновыми свойствами. Волновые свойства фотона проявляются в том, что для него нельзя точно указать, в какую именно точку экрана он попадет после про­хождения щели. Можно говорить лишь о вероятности попадания каждого фотона в ту или иную точку экрана.

Такое истолкование связи между волновыми и квантовыми свой­ствами света сыграло выдающуюся роль в развитии современной физики.

Волновые свойства микрочастиц. Корпускулярно-волновой дуализм присущ не только свету, но и частицам вещества. Эту идею высказал, исходя из соображений симметрии, Луи де Бройль: если свет, который рассматривался как электромагнитная волна, может проявлять корпускулярные свойства, то и частицы вещества должны проявлять волновые свойства.

Согласно этой идее, импульс частицы с массой m и скоростью υ равен р = mυ, а с другой стороны, он равен p= h/λ. Следо­вательно, движущейся частице можно поставить в соответствие волну с длиной: λ_Б =h/p= h/mυ.

Величину λ_Б называют дебройлевской дли­ной волны частицы. Экспериментально волно­вые свойства микрочастиц были обнаружены в опытах по дифракции электронов на кристаллах.

Наличие волновых свойств у частиц вносит ограничения в применимости к ним классиче­ской механики, согласно которой час­тица в любой момент времени занимает опре­деленное положение в пространстве и обладает определенным импульсом.

Когда проводится какое-либо измерение, его результат содержит некоторую неопределен­ность, обусловленную двумя факторами: корпускулярно-волновым дуализмом и неизбеж­ным взаимодействием наблюдаемого объекта с регистрирующим прибором, приводящим к изменению состояния объкта. Поэтому сущест­вует предел, ограничивающий точность измерений. Этот предел не зависит от степени совершенства измерительного прибо­ра, а присущ самой природе вещей. Это и есть принцип неопределенностей Гейзенберга.

Количественные соотношения, выражающие этот принцип для конкретных динамических пе­ременных, называются соотношениями неопре­деленностей. Наиболее важными являются два из них:

.

Первое соотношение утверждает, что нельзя измерить одновременно с абсолютной точностью положение (координату) и проекцию импульса микрочастицы на ту же ось. Чем точнее мы пытаемся определить положение объекта, т.е. чем меньше Δх, тем больше будет неопределенность импульса Δр_x . Этот вывод можно понять из следующих рассуждений: пусть мы хотим как можно точнее узнать положение микрочастицы (Δх→0 ). Для этого мы должны использовать фотоны с малой длиной волны λ (именно λ определяет точность измерения положения ∆х) и, соответственно, большим импульсом р_f = h/λ. В результате такого соударения двух частиц измеряемая частица приобретает непредсказуемый импульс. Если же мы попытаемся точно измерить проекцию импуль­са, то большой окажется неопределенность в по­ложении объекта. Принцип неопределенностей в то же время не запрещает точно определить что-то одно: либо положение, либо импульс. Можно так­же с абсолютной точностью измерить координату и проекции импульса на другие оси. Согласно этому соотношению неопределенностей: а) объяснена устойчивость атома; при гипотетическом падении электрона на ядро неопределенность положения электрона уменьшилась бы на 5 порядков с 10 ^–10 м (размер атома) до 10 ^–15 м (размер ядра). На 5 порядков соответственно увеличилась бы неопределенность импульса электрон и он, получив бы такую энергию, не смог бы удержаться в ядре; б) невозможно определить траекторию движения микрочастицы (для этого необходимо знать в каждый момент времени и координату и импульс частицы);

Второе соотношение устанавливает связь между неопределенностью энергии ΔE квазистационарного возбужденного состояния и средним временем жизни Δt возбужденного состояния в атомных процессах. Например, достаточно точно можно измерить энергию системы в стационарном состоянии, время жизни в котором велико (Δt → ∞), если же система находится в нестационарном состоянии, время жизни Δt в котором конечно, энергию можно измерить с погрешностью порядка ΔE ~ ħ /Δt .

Волновая функция, физический смысл и свойства. Состояние квантовой частицы нельзя определять, как в классической механике одновременным заданием в начальный момент времени координат и импульса . Это запрещено принципом неопределенностей. По аналогии с электромагнитной волной, для которой электромагнитное поле определяется заданием некоторой функции координат и времени E(x,y,z,t), для описания движения микрочастиц вводится некоторая функция координат и времени Ψ(x,y,z,t), характеризующая волну де Бройля, и получившая название волновой функ­ции (ВФ) .

Сама волновая функция Ψ в общем случае комплексна и поэтому не имеет наглядного физического представления, ее нельзя проде­монстрировать экспериментально. Согласно М.Борну, физический смысл имеет квадрат модуля ВФ , с помощью которого определяется вероятность dP того, что частица в момент времени t будет обнаружена в элементе объема dV, расположенном в окрест­ности точки х, у,z: .

Т.о, , где Ψ^* означает комплексно сопря­женную к Ψ величину, является плотностью веро­ятности.

Волну де Бройля можно рассматривать как волну вероятности, амплитудой которой является волновая функция.

Де Бройль постулировал, что свободное дви­жение частицы с определенной энергией E и импульсом описывается волновой функцией вида: . – мнимая единица.

Функция Ψ должна удовлетворять т.н. стандартным условиям. Она должна быть однозначной, поскольку микрочастица в определенный момент времени может находиться только в одной точке пространства. Волновая функция и ее частные производные по координатам являют­ся непрерывными во всех точках простран­ства (при движении частица не может исчезать в одном месте и появляться в другом). И наконец, волновая функция должна быть конечна, т.е. нигде не обращаться в бесконечность. Поскольку значение , вычисленное в некоторой точке, пропорционально вероятности Р обнаружения частицы, описываемой функцией Ψ, в этой точ­ке, то интеграл от по всему пространству должен быть конечным, так как в любом случае частица где-то должна быть. Обычно этот интеграл приравнивают единице: .

Волновую функцию, для которой выполняет­ся это соотношение, называют нормирован­ной, а само равенство – условием норми­ровки волновой функции.

Нахож­дение вида волновой функции частицы, движущейся под действием внешних сил, является основной задачей квантовой механики, так как задание волновой функции есть полное и исчерпывающее описание этой частицы. Это связано с тем, что вероятностное пове­дение микрочастиц лежит в самой их природе.

Уравнение Шредингера. Волны де Бройля описывают состояние только свободной частицы. В 1926 г. Э.Шредингер обобщил гипотезу де Бройля на случай движения микрочастицы во внешнем силовом поле и получил уравнение, описывающее поведение (распространение) волн вероятности во внешних силовых полях. Это уравнение, в результате решения которого получается конкретный вид ВФ, получи­ло название волнового уравнения, или уравнения Шредингера.

,

где m – масса частицы, U(x,y,z,t) – потенциальная функция частицы в силовом поле.

Как и все основные уравнения физики (напри­мер, законы Ньютона, уравнения Максвелла), уравнение Шредингера не имеет вывода. Пра­вильность уравнения Шредингера и толкование смысла фигурирующей в нем волновой функции подтверждаются огромным опытным материа­лом современной физики.

То, что уравнение Шредингера содержит лишь первую производную от Ψ по времени, связано с выражением принципа причинности: если известна волновая функ­ция Ψ(x,y,z,0), частицы в начальный момент времени, то можно однозначно определить ее волновую функцию Ψ(x,y,z,t) в любые последующие моменты времени t > 0. Однако, точное знание ВФ для какой-либо точки пространства позволяет определить лишь вероятность обнаружения микрочастицы в этой точке.

Часто потенциальная функция U частицы яв­ным образом не зависит от времени и в этом случае она имеет смысл потенциальной энергии. Силы, дей­ствующие на частицу, а следовательно, и U(х,у,z) за­висят только от координат. В этих случаях уравнение Шредингера можно упрос­тить, исключив всякую зависимость от t. Это получается, если ВФ представить в виде произведения координатной и временной частей: .

Подставив в зависящее от времени уравне­ние Шредингера это выражение и сократив все уравнение затем на общий экспоненциаль­ный множитель, получим: , где - т.н. оператор Лапласа.

Это уравнение называется уравнением Шре­дингера для стационарных состояний.

Волновое уравнение Шредингера играет в квантовой механике ту же роль, что 2 закон Ньютона в классической механике. Задать закон движения частицы в квантовой механике – зна­чит определить Ψ-функцию в каждый момент времени в каждой точке пространства.

Так как уравнение Шредингера является урав­нением второго порядка в частных производ­ных, то для его решения необходимо задавать на­чальные и граничные условия.

Квантовая частица в потенциальной яме. Рассмотрим одномерное (вдоль оси х) движение частицы в потенциальном поле, называющемся беско­нечно глубокой прямоугольной потенциальной ямой шириной ℓ: .

Так как энергия частицы Е не может быть бес­конечной, частица не может находиться вне ямы, поэтому вероятность ее обнаружения вне ямы, а значит, и волновая функция, равна нулю: w(x<0)=w(x>ℓ) и ψ(x<0)=ψ(x>ℓ)=0.

Из условия непрерывности ВФ вытекает равенство нулю ВФ и на границе ямы: ψ(x=0)=ψ(x=ℓ)=0. Это граничные услови­я для решения уравнения Шредингера для частицы внутри потенциальной ямы: ,

где Е — энергия частицы.

Решение такого дифференциального уравне­ния имеет вид: ψ=A·sin(k·x),

где - волновое число. Используя граничное условие ψ(ℓ)=0, получим: κ_n ·ℓ=n·π ,

где n=1,2,3,... – любое целое число, большее нуля (квантовое число). Это условие позволяет найти возможные значения энергии частицы

.

Уравнение Шредингера имеет решения, удов­летворяющие граничным условиям только при дискретных значениях квантового числа п. Энер­гия частицы в бесконечно глубокой потенциаль­ной яме оказывается квантованной. Состояние частицы с наименьшей возможной энергией (n=1) называется основным, все остальные состоя­ния – возбужденными. Волновая функция, отвечающая n-му уров­ню энергии: . Постоянную А_n определим из условия нормировки ; и .

На границах ямы при х = 0 и х = ℓ всегда |ψ_n| ² = 0, однако, вeроятность нахождения частицы в определенной точке внутри ящика может сильно меняться при разных значениях квантового числа п .

Выводы: энергия микрочастицы, движущей­ся в потенциальной яме, пробегает дискретный ряд значений; даже в основном состоянии час­тица не находится в состоянии полного покоя; дискретный характер энергетических уровней проявляется при малой массе частиц и малых размерах области, в которой происходит движе­ние; при больших значениях квантовых чисел и пространственно неограниченном движении квантовомеханические соотношения переходят в формулы классической физики.

Квантовым гармоническим осциллятором называется микрочастица массы т, находящаяся в параболической потенциальной яме вида U(x)=κ·x²/2 и совершающая гармоническое движение с частотой ω; κ-постоянная.

Модель квантового ос­циллятора особенно полезна при исследова­нии малых колебаний систем около положения равновесия, например, колебаний атомов в уз­лах кристаллической решетки или колебаний атомов около их положений равновесия в мо­лекуле.

По аналогии с классической теорией (пружинный маятник) положим . Тогда для потенциальной энергии по­лучим:

. Стационарное уравнение Шредингера в дан­ном случае будет иметь вид:

.

Полученное уравнение имеет конечные, од­нозначные и непрерывные решения, т.е. собственные функции, не для всех значений энергии Е, а только при собственных значениях, удовлетворяющих условию:

Число n_υ называется колебательным кванто­вым числом. Из последнего равенства следу­ет, что энергия квантового осциллятора кванту­ется. Энергетический спектр представляет собой эквидистантные, т.е. отстоящие друг от друга на одинаковую величину ΔE=ħω, уровни. Минималь­ная энергия, которой может обладать квантовый осциллятор, равна Е₀ = ħω / 2 и называется энер­гией нулевых колебаний, или нулевой энергией и соответствует абсолютному нулю температур.

То, что минимальная энергия осциллятора не может быть равна нулю даже при 0К, находится в соответ­ствии с признанием относительности покоя и вечности движения. Если бы энергия частицы равнялась нулю, то это озна­чало бы, что частица покоится и ее импульс и координата одновременно имеют точные значения, что противоречит принци­пу неопределенностей. Существование нулевых колебаний доказы­вают опыты по наблюдению рассеяния света прозрачными кристаллами при сверхнизких (вплоть до 10 ^{– 6}К) температурах.

Расчет показывает, что для квантового осцил­лятора возможны переходы только между сосед­ними уровнями, т.е. с изменением квантового числа n_υ на единицу:

Δ n_υ = ±1.

Это условие называется правилом отбора, оно показывает, какие из всех мыслимых переходов реализуются в действительности.

При каждом из переходов излучается или по­глощается фотон (или другая частица – фонон) с энергией ħω , где ω – его цик­лическая частота.