2. Всякое изменяющееся во времени элект­рическое поле порождает вихревое магнитное поле.

Тогда полевые уравнения Максвелла в интегральной форме и­меют вид:

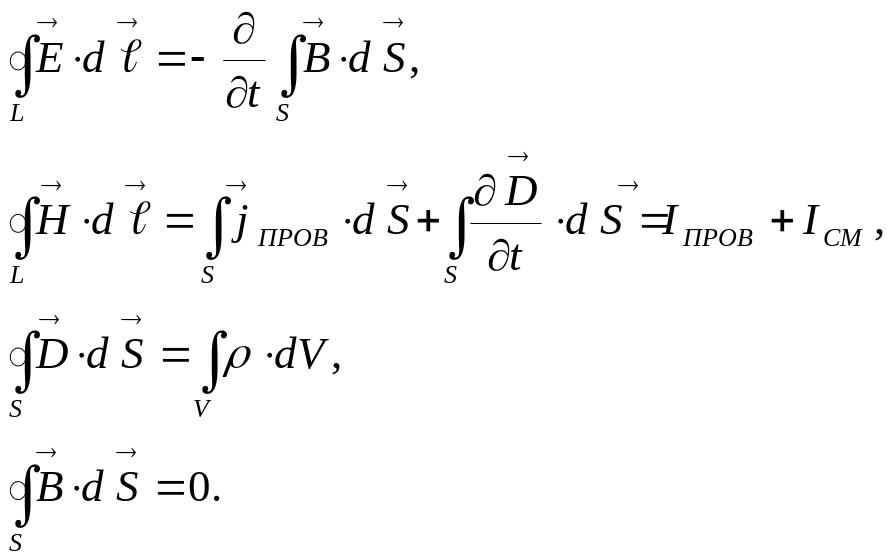
Первое уравнение связывает значение скоро­сти изменения магнитного потока через любую поверхность S и циркуляцию вектора напряженно­сти электрического поля по контуру L, опираю­щемуся на эту поверхность. Оно является по су­ществу выражением закона электромагнитной индукции Фарадея.

Второе уравнение устанавливает связь между токами проводимости и смещения и порождаемым ими магнитным полем; оно указывает, что переменное электрическое поле приводит к по­явлению магнитного поля. Таким образом, мы должны считать, что магнитное поле созда­ется не только токами проводимости, но и токами смещения. Это очень важный результат, так как токов проводимости может вообще не быть (например, в вакууме), но если есть электрическое поле и оно меняется со временем , то и в этом случае появ­ляется магнитное поле. Это обобщенный закон Био-Савара-Лапласа..

Третье уравнение представляет собой теоре­му Гаусса в электростатике и указывает, что линии индукции электрического поля не замкну­ты и что источником электростатического поля служат электрические заряды.

Четвертое уравнение представляет теорему Гаусса для магнитного поля и указывает на то, что линии индук­ции магнитного поля являются замкнутыми, т.е., что в природе нет одиночных магнитных зарядов (монополей).

Из уравнений Максвелла следует, что электри­ческое и магнитное поля нельзя рассматривать как независимые, изменение во времени одного из этих полей приводит к появлению другого.

Чтобы использовать уравнения Максвелла для расчета полей, к ним нужно еще добавить уравнения, характеризующие свойства среды (материальные уравнения), в которые входят диэлектрическая проницаемость ε, магнитная проницаемость μ и электропровод­ность σ среды.

Для изотропных сред, не содержащих сегнетоэлектриков и фер­ромагнетиков.:

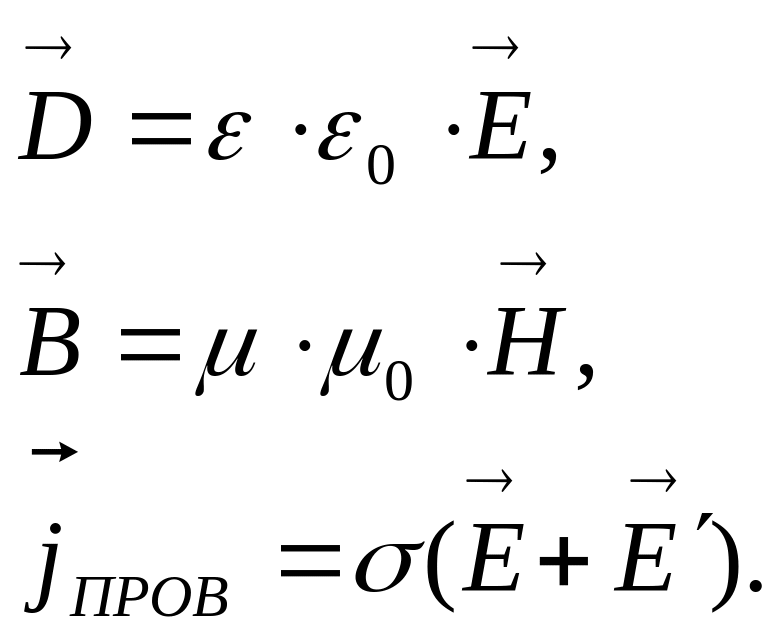
Последняя формула – это закон Ома в дифференциальной форме.

7. Электромагнитные колебания

Незатухающие колебания

Свободные (собственные) электриче­ские колебания — колебания, совершающие­ся без внешнего воздействия за счет первона­чально накопленной энергии. Такие колебания совершаются в контуре, состоящем из катушки индуктивности L и конденсатора C. Если конденсатор предва­рительно зарядить, а потом подключить к катуш­ке, то он будет разряжаться через катушку ин­дуктивности. Ток разрядки создает магнитное поле в катушке. Магнитное поле, в свою очередь, за счет возникновения э.д.с. самоиндукции обеспечит перезарядку конденсатора. В каждый момент времени напряжения на катушке U_L и конденса­торе U_C равны друг другу, т.е. U_C + U_L=0 . Тогда уравнение колебаний в таком контуре имеет вид: . Если учесть, что заряд на конденсаторе q и ток в цепи I связаны соотношением I= - dq/dt (уменьшение заряда на конденсаторе приводит к возрастанию тока в цепи и наоборот), приходим к уравнению свободных гармонических незатухающих колебаний: где частота собственных колебаний:

Решением его является q=q₀·cos(ω₀·t+φ₀). Сила тока в цепи изменяется по закону I= – dq/dt= q₀·ω₀·sin( ω₀·t + φ₀)=I₀· sin( ω₀·t + φ₀), где – амплитуда тока. При свободных гармонических колебаниях в колебательном контуре происходит периодическое преобразование энергии W_e электрического поля конденсатора в энергию магнитного поля W_m катушки и наоборот: ; .

Полная энергия электромагнитных колебаний в контуре не изменяется с течением времени и равна: .

Затухающие колебания

Реальный колебательный контур имеет оми­ческое сопротивление R, поэтому колебания в нем затухают, т.к. энергия, запасенная в контуре, выделяется в виде тепла. Уравнение затухающих колебаний в RLC-контуре имеет вид : где β=R/(2·L) – коэффициент затухания.

В кон­туре возникнут колебания при условии: , т.е., при L > C·R²/4. Решение уравнения колебаний имеет вид: , где Затухание колебаний характеризуют логарифмическим декрементом затухания и добротностью . Если значение индуктивности L ≤ C·R²/4 , то э.д.с. самоиндукции оказывается недостаточ­ной, чтобы вызвать перезарядку обкладок кон­денсатора, процесс будет апериодическим. Сопротивление контура, при котором колебательный процесс переходит в апериодический (ω₀ = β), называется критическим: .

Вынужденные электрические колебания

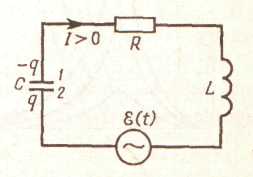Чтобы поддерживать в контуре колебания, надо извне подводить энергию, компенсирующую потери. Для этого необходимо, разорвав кон­тур, подать на образовавшиеся контакты пере­менное напряжение : ε(t) =U₀·cosΩt.

Уравнение вынужденных колебаний под действием этого вынуждающего напряжения имеет вид:

Решением полученного дифференциального уравнения будет выражение

q₀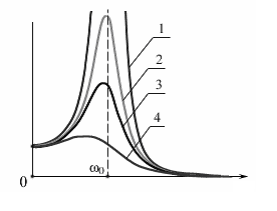

где значения амплитуды и фазы зависят от соот­ношения между частотой Ω вынуждающего воздействия и частотой собственных колебаний ω₀ :

β

Ω

и . При некото­рой частоте Ω наступает резонанс – резкое усиление амплитуды колебаний. Максимум заряда на конденсаторе достигается при резо­нансной частоте . Резонансные кривые для заряда совпадают с резонансными кривыми для механических колебаний . На рис. кривые 1-4 приведены для возрастающего коэффициента затухания β. Кривая 1 соответствует отсутствию затухания β=0.

Сила тока при вынужденных колебаниях изменяется со временем согласно выражению: I= - dq/d t= q₀·Ω·sin( Ω·t - φ)=I₀· sin( Ω·t – φ). Резонансная частота для силы тока совпадает с собственной частотой

Ω_РЕЗ=ω₀=1/LC , а амплитуда силы тока принимает значение I_0МАХ=U₀/ R.

Р

Ω

езонансные кривые для амплитуды силы тока I₀ для различных сопротивлений контура приведены на рис.

( По своему виду уравнения свободных незатухающих, затухающих и вынужденных колебаний такие же, как для механических колебаний. Поэтому, в принципе, все параметры электромагнитных колебаний в контуре можно получить, если учесть, что для них : и β=R/(2·L) ).