- •Билет №1
- •1.Функция двух переменных. Определение. Примеры функций. Предел и непрерывность функции. Теоремы о свойствах непрерывных функций. (сформулировать)
- •Билет №2
- •1.Частные производные. Определение. Формулы и правила для их вычисления.
- •Билет №3
- •1.Дифференциируемость и дифференциал функции двух переменных. Необходимые условия дифференцируемости. (Доказать)
- •Билет №4
- •1.Теорема о достаточных условиях дифференцируемости функции двух переменных. (Доказать)
- •Билет №5
- •1.Производные от сложных функций двух переменных (доказать формулы). Полная производная.
- •Билет №6
- •1.Производные второго порядка и дифференциал второго порядка функции двух переменных.
- •Билет №7
- •1.Экстремум функции двух переменных. Необходимое условие экстремума (доказать). Достаточные условия экстремума. (Сформулировать)
- •Билет №8
- •1.Скалярное поле. Производная по направлению: определение, формула для вычисления (доказать). Градиент: определение, его связь с производной по направлению (доказать формулу).
- •Билет №9
- •1.Неявная функция. Определение, примеры. Теорема о существовании и дифференцируемости неявной функции (сформулировать).
- •Билет №10
- •1.Первообразная и неопределенный интеграл (определения). Свойства неопределенного интеграла. Таблица основных интегралов.
- •Билет №11
- •1.Непосредственное интегрирование. Теорема об инвариантности формул интегрирования (доказать). Подведение под знак дифференциала.
- •Билет №12
- •1.Интегрирование методом замены переменной (доказать формулу). Интегрирование по частям.
- •Билет №13
- •1.Интегрирование дробно-рациональных функций.
- •Билет №14
- •Билет №15
- •1.Определенный интеграл. Определение, геометрический смысл.
- •Билет №16
- •1.Свойства определенного интеграла (перечислить, теорему о среднем доказать).
- •Билет №17
- •1.Определенный интеграл с переменным верхним пределом. Определение. Теорема об его производной (доказать). Формула Ньютона-Лейбница (доказать).
- •Билет №18
- •1.Замена переменной в определенном интеграле (доказать формулу). Интегрирование по частям.
- •Билет №19
- •Билет №20
- •Билет №21
- •1.Дифференциальные уравнения с разделяющимися переменными. Определение, их решение.
- •Билет №22
- •1.Дифференциальные уравнения первого порядка с однородными функциями. Определение, их решения.
- •Билет №23
- •1.Линейные дифференциальные уравнения первого порядка. Решение методом вариации произвольного постоянного.
- •Билет №24
- •1.Дифференциальные уравнения, допускающие понижение порядка.
- •Билет №25
- •Билет №26
- •1.Понятие о линейной независимости функций. Определитель Вронского для функций. Теорема о необходимом условии линейной зависимости двух функций (доказать).
- •Билет №27
- •1.Необходмое и достаточное условие линейной независимости двух решений однородного линейного дифференциального уравнения второго порядка.
- •Билет №28
- •Билет №29
- •1.Линейные однородные дифференциальные уравнения 2-ого порядка с постоянными коэффициентами. Построение их общего решения в зависимости от корней их характеристического уравнения.
- •Билет №30
- •1.Неоднородные линейные дифференциальные уравнения 2-ого порядка. Теорема об общем решении (доказать). Теорема о частном решении, если правая часть уравнения есть сумма двух функций.
- •Билет №31
- •1.Способ неопределенных коэффициентов для нахождения частного решения линейного дифференциального уравнения 2-ого порядка с постоянными коэффициентами.
Билет №19
1.Геометрические приложения определенного интеграла. Вычисление площадей в прямоугольных координатах. Вычисление длин дуг, заданных в прямоугольных координатах уравнением y=f(x), x [a,b] и заданных параметрически. Доказать соответствующие формулы.
1.Вычисление площадей в прям координатах.
1) если f(x) непрерывная и неотрицательная на отрезке [a,b] ф-ия, то площадь криволинейной трапеции аАвВ вычисляется по формуле S=
2) если f(x)
меняет знак на отрезке [a,b],
то отрезок [a,b]
следует разделить на части, в каждой из
которых f(x)
сохраняет знак. Площади фигур, находящихся
над осью 0х берут со знаком плюс, а площади
фигур под осью 0х со знаком минус: Q1=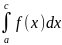 ,
Q2= -
,
Q2= - ,
Q3=
,
Q3= .
Тогда площадь криволинейной трапеции
аАвВ равна: S=Q1+Q2+Q3=
.
Тогда площадь криволинейной трапеции
аАвВ равна: S=Q1+Q2+Q3= .
.
3)криволинейная
трапеция АВСД ограничена и снизу, и
сверху непрерывными кривыми, ур-я которых
у1=f(x),
y2=g(x),
х
[a,b],
причем f(x)≥
g(x)≥0.
Рассматривая криволинейную тарпецию
АВСД как разность фигур аСДв и аАВв,
получим: SABCD=
-
= .
.
4)если g(x) меняет знак на отрезке [a,b], то площадь криволинейной трапеции АВСД вычисляется также по формуле SABCD= - =
2.Вычисление длин дуг.
1) пусть плоская кривая АВ задана в прям координатах ур-ем у=f(x), х [a,b]. Рассмотрим Т-произвольное разбиение отрезка[a,b]. Пусть х0=а<х1<х2<…<хn=b- точки разбиения, λ(Т) – параметр разбиения. Обозначим А, А1, А2,…,В, тчки на дуге АВ с абсциссами соответственно х0,х1,х2,…,xn. Соединим последовательно точки А, А1, А2,…,В прямолинейными отрезками. Получим ломанную Л= А, А1, А2,…,В вписанную в дугу АВ. Обозначим: ΔSi, 1≤i≤n, длину каждого звена ломаной Аi-lAi; L(T)-длину ломаной, которая образуется при данном разбиении отрезка Т отрезка [a,b].
Длина ломаной
равна L(T)=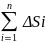 =
=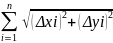 ,
где Δyi=f(xi)-f(xi-1).
,
где Δyi=f(xi)-f(xi-1).
Опред: Если
сущ-ет
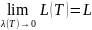 ,
то кривая АВ называется спрамляемой, а
число L называется длиной
дигу АВ. «на языке ε-δ»: для
ε>0
δ>,
такое что для
такого, что λ(Т)<δ выполняется неравенство
,
то кривая АВ называется спрамляемой, а
число L называется длиной
дигу АВ. «на языке ε-δ»: для
ε>0
δ>,
такое что для
такого, что λ(Т)<δ выполняется неравенство
 <ε.
<ε.
Теорема:
Пусть f(x),
f’(x)непрерывны
на [a,b],тогда
кривая АВ спрамляема и L=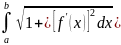 .
.
Док-во:
По т Лагранжа
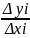 =f’(c),
xi-1<c<xi.
Поэтому ΔSi=
=f’(c),
xi-1<c<xi.
Поэтому ΔSi= =
= Δxi=
Δxi= Δxi,
xi-1<c<xi.
Длина вписанной ломаной: L(T)=
=
Δxi,
xi-1<c<xi.
Длина вписанной ломаной: L(T)=
= Δxi,.
В правой части равенства интегральная
сумма для ф-ии ф(х)=
на [a,b]. Т.к.
по условию f’(x)
непрерывна на [a,b],
то и ф(х) непрерывна на [a,b].
Поэтому сущ-ет
Δxi,.
В правой части равенства интегральная
сумма для ф-ии ф(х)=
на [a,b]. Т.к.
по условию f’(x)
непрерывна на [a,b],
то и ф(х) непрерывна на [a,b].
Поэтому сущ-ет
 =
= =
= =
=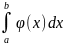 =
=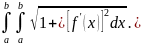
2.Кривая заданная параметрическими ур-ми.
 ,где
t
[α,β].
(1)
,где
t
[α,β].
(1)
Каждому
значению t0 из [α,β]
ур-я (1) приводят в соответствие пару
чисел х0= и
у0=
и
у0= .
Числа х0 и у0 можно рассматривать как
прямоугольные координаты точки на
плоскости. Когда t изменяется
от α до β, точка на плоскости описывает
некоторую кривую АВ.
.
Числа х0 и у0 можно рассматривать как
прямоугольные координаты точки на
плоскости. Когда t изменяется
от α до β, точка на плоскости описывает
некоторую кривую АВ.
Теорема. Пусть ф-ии φ(t), ψ(t) имеют производные на [α,β]. Тогда параметрические ур-я (1) определяют однозначную и дифференцируемую ф-ию у от х, причем dy/dx=φ’(t)/ψ’(t).
Док-во:
По условию сущ-ет φ’(t) на [α,β]→ φ(t) непрерывна на [α,β]. Т.к. φ’(t) знакопостоянна на [α,β], то φ(t) строгомонотонна на [α,β]. Т.о. φ(t) непрерывна и строгомонотонна. Поэтому, эта ф-ия имеет обратную дифференц ф-ию t=Ф(х), причем Ф’(х)=1/ φ’(t).
Тогда у= ψ(t)= ψ[Ф(х)] есть сложная ф-ия от х. По правилу дифференцирования сложной ф-ии: dy/dx=ψ’t* Ф’(х)= ψ’(t)/φ’(t).
Пусть а=ф(α),
в=ф(β). В интеграле L=
выполним замену переменной х= φ(t)
и dx= φ’(t)dt.
Получим: L=
=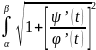 *
φ’(t)dt=
*
φ’(t)dt=