Билет №1

1.Функция двух переменных. Определение. Примеры функций. Предел и непрерывность функции. Теоремы о свойствах непрерывных функций. (сформулировать)

Опр: если в каждой точке М(х,у) из некоторого множества Е точек плоскости оху ставится в соответствие по известному закону число U, то говорят, что на множестве Е задана ф-я U=f(х,у) и U=f(х,у) – есть ф-я двух переменных.

Множество Е называется областью определения ф-ии. Если ф-я задана аналитически, то обл опр состоит из тех точек, для которых формула имеет смысл.

Примеры ф-й: Z=x²+y², Е-вся плоскость.

Z=√1- x²-y², формула годится только для тех точек М(х,у), которые удовлетворяют неравенству 1-x²-y²≥0 или x²+y²≤1. Здесь Е – это замкнутый круг с центром в точке (0,0) и радиусом 1.

Предел и непрерывность ф-ии. Пусть ф-я U=f(М) определена в некоторой окрестности точки М₀, в точке М₀ ф-я может быть неопределена.

Опр1: число А называется пределом ф-ии U=f(М) при стремлении точки М к точке М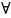₀, ε>0 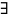U_δ(М₀), такая что М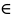 U_δ(М₀) (М≠М₀) выполняется неравенство |f(М)-А|<ε.

Обозначение: 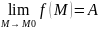или

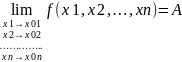
Опр2: ф-я U=f(М) называется непрерывной в точке М₀, если она определена в этой точке и некоторой ее окрестности и 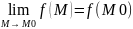. Если в точке М₀ не выполняются условия непрерывности, то М₀ называется точкой разрыва ф-ии f(М). Точки разрыва могут быть изолированными, образовывать линии разрыва, поверхности разрыва.

Опр3: ф-ия U=f(М) называется непрерывной на множестве Е, если она непрерывна в каждой точке этого множества.

Теоремы:

1.Пусть Ф-Ии f(M) и g(M) непрерывны в т.А. Тогда ф-ии f(M)±g(M), f(M)*g(M) и f(M)/g(M) (если g(A)≠0) также непрерывны в т.А.

2.Теорема об устойчивости знака непрерывной ф-ии. Пусть ф-ия f(M) непрерывна в т.А. Тогда U_δ(А), в которой ф-ия сохраняет знак f(А).

3.Первая теорема Вейерштрасса. Пусть ф-ия f(M) непрерывна на замкнутом ограниченном множестве Е. Тогда она ограничена на этом множестве.

4.Вторая теорема Вейерштрасса. Пусть ф-ия f(M) непрерывна на замкнутом ограниченном множестве Е. Тогда она принимает хотя бы в одной точке множества Е наибольшее значение и, хотя бы в одной точке, наименьшее значение.

5.Теорема об обращении ф-ии в нуль. Пусть ф-ия f(M) непрерывна в связной области Е. Если в двух точках М₁ и М₂ области Е ф-ия принимает значения разных знаков, например, f(М₁)<0, f(М₂)>0, то в этой области найдется точка М₀ такая, что f(М₀)=0.

Билет №2

1.Частные производные. Определение. Формулы и правила для их вычисления.

Пусть ф-ия Z=f(x,y) определена в точке М₀(х₀,у₀) и некоторой ее окрестности. Независимой переменной х дадим приращение Δx, оставив то же значение у₀ другой независимой переменной у. Тогда ф-ия получит приращение Δ_xZ=f(х₀+Δx,у₀)-f(х₀,у₀),которое называется частным приращением ф-ии по х. Аналогично определятся частное приращение ф-ии по у Δ_уZ=f(х₀,у₀+Δу)-f(х₀,у₀).

Если обе независимые переменные получат приращения Δx и Δу, то ф-ия Z=f(x,y) получит приращение ΔZ= f(х₀+Δx,у₀+Δу)-f(х₀,у₀), которое называется полным приращением ф-ии.

Опред: если сущ-ет 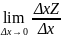, то его значение называется частной производной ф-ии f(x,y)по х в точке М₀(х₀,у₀). Частную производную обозначают одним из символов:

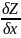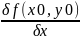, , Z’x, f’(x₀,y₀,z₀), .

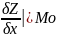Аналогично, 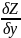= 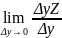- частная производная ф-ии f(x,y)по у в точке М₀(х₀,у₀).

Из определения: формулы и правила для вычисления частных производных совпадают с формулами и правилами, указанными для ф-ии одной переменной, но нужно помнить, чт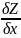о вычисляется в предположении, что у-постоянная, а в предположении, что х-постоянная. Частные производные для ф-ии любого числа переменных определяются аналогично.