Билет №11
1.Непосредственное интегрирование. Теорема об инвариантности формул интегрирования (доказать). Подведение под знак дифференциала.
Непосредственное интегрирование состоит в том, что заданный интеграл преобразуется к табличному путем тождественного преобразования подынтегрального выражения и использования линейных св-в интегралов.
Теорема об
инвариантности формул интегрирования:
все формулы интегрирования не зависят
от характера переменной интегрирования.
Если
=F(x)+C
(1), U=φ(x)-любая
дифференцируемая ф-ия.Тогда
=F(U)+C
(2).
Док-во:
Из (1) получаем: f(x)dx=dF(x) (взяли дифференциалы от обеих частей)
Св-ва инвариантности дифференциалов 1ого порядка: формула не меняется, если вместо х подставили дифференцируемую ф-ию U= φ(x).
dF(U)=f(U)dU,
=
или
=F(U)+C
(св-во 3 интеграла).
К непосредственному интегрированию относят и подведение под знак дифференциала.
По определению дифференциала ф-ии: φ’(x)dx=d[φ(x)]. Преобразование по этой формуле называется подведением множителя φ’(x) под знак дифференциала.
Таблицу подведения под знак дифференциала для основных элемент ф-ий легко получить из таблицы интегралов, по св-ву: если =F(x)+C, то f(x)dx=dF(x).
Пример:
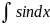=-cosx+C,
sinxdx=-d(cosx)
При интегрировании подведением под знак дифференциала используют св-ва дифференциала:
1.d[φ(x)]=d[φ(x)+C]
2.d[Cφ(x)]=Cd[φ(x)]
3.d[φ(x)]=1/C d[Cφ(x)]
Билет №12
1.Интегрирование методом замены переменной (доказать формулу). Интегрирование по частям.
Метод замены переменных.
Пусть непосредственно вычислить не удается. Часто путем удачной замены переменной интеграл сводится к интегралу, который легко вычисляется.
Сделаем замену х=φ(t), потребуем, чтобы ф-ия удовлетворяла условиям:
1.ф-ия φ(t) непрерывна и строго монотонная на промежутке Т→сущ-ет обратная ф-ия t=φ(x) на Х(множество значений ф-ии φ(t) на промежутке Т)
2.ф-ия φ(t) имеет непрерывную производную φ’(t) на Т.
Тогда имеет
место формула:
=
*
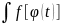φ’(t)dt
(1), т.е. если
*
φ’(t)dt=F(t)+C
(2), то
=F[ψ(x)]+C
(3)
Док-во:
Из (2): F’(t)=f[φ(t)]*φ’(t)=f(x)*φ’(t)
Чтобы док-ть (3) надо показать, что производная от правой части равна подынтегральной ф-ии.
Правило для отыскания производной сложной ф-ии:
dF[ψ(x)]/dx=dF/dt dψ(x)/dx=f(x)*φ’(t)*1/φ’(t)=f(x)
По правилу производной для обратной ф-ии: dψ(x)/dx=1/φ’(t).
По частям.
Пусть U(x)и V(x)-дифференцируемые ф-ии.
d(UV)=UdV+VdU
UdV=d(UV)-VdU→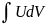
=UV-
- формула интегрирования по частям.
Для применения
этой формулы нужно подынтегральное
выражение в виде произведения UdV,
так чтоб вычисления
и
была легче, чем вычисления исходного
интеграла.
Рекомендации: 1. Если под знаком ∫ стоит алгебраический многочлен, умноженный на тригонометрическую или показательную ф-ию, то за U надо брать многочлен, а всё остальное за dV.
2.Если под знаком ∫ есть логарифмическая или обратная тригонометрическая ф-ия, то ее нужно брать за U, а всё остальное за dV.
Билет №13
1.Интегрирование дробно-рациональных функций.
Дробно-рациональные ф-ии-основной класс интегрируемых ф-ий, т.е. таких ф-ий, интегралы которых выражаются через элементарные ф-ии. Дробно-рациональные ф-ии: R(x)=Pn(x)/Qm(x), где Pn(x)=a0+a1x+…+anxn, Qm(x)= b0+b1x+…+bnxn. Если n<m, то дробь R(x)-правильная, n≥m, то дробь неправильная.
Всякую неправильную дробь можно представить в виде суммы алгебраического многочлена и правильной дроби, путем деления многочлена в числителе на многочлен в знаменателе. Т.к. интегрирование многочленов не вызывает трудностей, то задача интегрирования рациональной дроби сводится к правильной рациональной дроби.
Опред: правильные рац дроби вида: А/(х-а), В/(х-а)к, (Ах+В)/(х2+рх+q), где А,В,а,р,q-некоторые числа и х2+рх+q не разлагается на линейные множители, т.е. D=(p/2)2-q<0 называются простейшими рац дробями 1ого,2ого и 3его типа.
Интегрирование
дробей 1ого и 2ого типов не вызывают
трудностей:
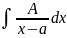=A
ln|x-a|+C
(1),
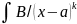dx=B
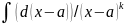=B(x-a)-k+1/(1-k)
+C (2)
Интегрирование дробей 3его проводится непосредственно.
Теорема: каждая правильная дробь Pn(x)/Qm(x) может быть представлена в виде суммы конечного числа простейших дробей.
Разложение правильной дроби на простейшие определяется разложением её знаменателя Qm(x) на простые множители.
Известно, что всякий алгебраический многочлен разлагается единственным образом на множители типа х-а и квадратичные множители х2+рх+q, которые D=p2/4-q<0.
В разложении знаменателя пр.дроби:
1.всякому неповторяющемуся линейному множителю х-а соответствует одна дробь 1ого типа
2.всякому повторяющемуся линейному множителю (х-а)к соответствует к-дробей. Одна 1ого типа и (к-1) дробь 2ого типа.
3.всякому квадратичному множителю х2+рх+q отвечает 1дробь 3его типа.