Билет №5

1.Производные от сложных функций двух переменных (доказать формулы). Полная производная.

Пусть ф-ии U=f(x;y) и V=φ(x;y) дифференцируемы в точке М₀(х₀,у₀), а ф-ия Z=F(U;V) дифференцируема в точке N₀(U₀,V₀) причем U₀=f(х₀,у₀), V₀=φ(х₀,у₀). Докажем, что сложная ф-ия Z=F[f(x;y);φ(x;y)] имеет частные производные δz/δx и δz/δy в точке М₀.

Док-во:

Даём Δx, у=у₀, получим Δ_xU, Δ_xV (частные приращения) и z получит Δz.

Δz= δz/δU Δ_xU+ δz/δV Δ_xV+α(Δ_xU,Δ_xV)Δ_xU +β(Δ_xU,Δ_xV)Δ_xV

α,β→0 при Δ_xU→0, Δ_xV→0

Δz/Δx= δz/δU Δ_xU/Δx+ δz/δV Δ_xV/Δx+ (α Δ_xU/Δx+β Δ_xV/Δx)→0

Пусть Δx→0; Δ_xU,Δ_xV→0 (U,V диффер в т. М₀→непрерывны)

α,β→0

δz/δx=δz/δU δU/δx+ δz/δV δV/δx

Дадим Δу, оставив х= х₀

δz/δy= δz/δU δU/δу+ δz/δV δV/δу

δz/δU, δz/δV в точке N₀

δU/δx, δU/δу, δV/δx, δV/δу в точке М₀.

Замечание:

Рассмотрим частный случай Z=F(U;V), U=f(x), V=φ(x).

Z=F[f(x);φ(x)]

δz/δx= δz/δU δU/δx+ δz/δV δV/δx – формула для отыскания полной производной.

Билет №6

1.Производные второго порядка и дифференциал второго порядка функции двух переменных.

Пусть z=f(x,y), (x,y) D и дифференцируема в каждой точке этой области(имеет частные производные δz/δx и δz/δy в области D)

Пусть в точке М₀(х₀,у₀) сущ-ет δ/δx(δz/δx)=δ²z/δx² или z’’_xx – частная производная 2ого порядка.

δ/δy(δz/δх)= δ²z/δyδx;

δ/δх(δz/δy)= δ²z/δхδу-смешанные частные производные.

δ/δy(δz/δу)= δ²z/δy²

Аналигично определяются частные производные n-ного порядка.

Теорема о смешанных производных:

Пусть z=f(x,y) имеет частные производные δz/δx, δz/δy, δ²z/δхδу, δ²z/δyδx в окрестности U(M₀), причем δ²z/δхδу и δ²z/δyδx непрерывны в т.М₀.

Тогда δ²z/δхδу=δ²z/δyδx.

Замечание: если условие непрерывности δ²z/δхδу и δ²z/δyδx в т.М₀ не выполняется, то эти производные могут быть различны в т.М_0.

Пусть ф-ия z=f(x,y), (x,y) D и дифференцируема в каждой точке этой области(имеет частные производные δz/δx и δz/δy в области D). Тогда в каждой точке области можно посчитать дифференциал.

dz= δz/δх*dx+ δz/δy*dy

dz зависит:1.от точки М(х,у); 2.от dx и dy.

Будем считать, что dx, dy – const, независимо от точки, в которой будем считать. dz=dz(x,y)

Пусть данная ф-ия имеет в обл D непрерывные частные производные 2ого порядка.

Покажем, что тогда dz имеет непрерывные частные производные 1ого порядка в обл.

δ/δх(dz)= δ/δх[δz/δх*dx+ δz/δy*dy]= δ²z/δx²*dx+ δ²z/δy²*dy –ф-ия непрерывна.

δ/δy(dz)= δ/δy[δz/δх*dx+ δz/δy*dy]= δ²z/δyδx*dx+ δ²z/δy²*dy – ф-ия непрерывна.

По теореме о достаточных условиях дифференцируемости ф-ия dz будет дифференцируема в каждой точке области D, поэтому можно говорить о дифференциале этой ф-ии.

d(dz)=d(δz/δх*dx+ δz/δy*dy)=δ/δх[δz/δх*dx+δz/δy*dy]dx+δ/δy[δz/δх*dx+δz/δy*dy]dy= δ²z/δx²*dx²+δ²z/δхδу*dydx+δ²z/δyδx*dxdy+δ²z/δy²*dy²=δ²z/δx²*dx²+2δ²z/δхδу*dydx+δ²z/δy²*dy²=d²z.

Дифференциалы ф-ии zпорядка выше 1ого определяются таким же образом.

Билет №7

1.Экстремум функции двух переменных. Необходимое условие экстремума (доказать). Достаточные условия экстремума. (Сформулировать)

Пусть ф-ия z=f(x,y), (x,y) D. М₀(х₀,у₀) – внутренняя точка этой области.

Опред1: Точка М₀(х₀,у₀) называется точкой максимума ф-ии z=f(x,y),если U(М₀) такая, что f(х₀,у₀)> f(x,y) (x,y) U(М₀).

Опред2: Точка М₀(х₀,у₀) называется точкой минимума ф-ии z=f(x,y),если U(М₀) такая, что f(х₀,у₀)< f(x,y) (x,y) U(М₀). Если ф-ия имеет максимум или минимум в данной точке, то говорят, что она имеет экстремум в данной точке.

Теорема «Необходимые условия экстремума»: если ф-ия z=f(x,y) имеет экстремум в М₀(х₀,у₀), то каждая частная производная δz/δx и δz/δy в этой точке равна 0 или не сущ-ет.

Док-во:

Пусть в М₀(х₀,у₀) ф-ия имеет максимум. Тогда U(М₀) такая, что f(х₀,у₀)> f(x,y) (x,y) U(М₀). Будем сохранять значение у=у₀, а значение х будем менять, т.е. будем рассматривать ф-ию на прямой у=у₀. Тогда мы будем иметь ф-ию f(x,y₀) одной переменной х. Если точка М(x,y₀) U(М₀), то выполняется неравенство f(х₀,у₀)> f(x,y₀). А это означает, что ф-ия одной переменной f(x,y₀) имеет максимум в точке х₀, следовательно ее производная ( )(х=х₀ у=у₀)=0 или не сущ-ет.

Точки, в которых δz/δx и δz/δy равны 0 или не сущ-ют называются критическими точками ф-ии z=f(x,y). Если ф-ия z=f(x,y) имеет точки экстремума, то они находятся только среди критических точек. Но не всякая критическая точка является точкой экстремума.

Теорема «Достаточные условия экстремума»: Пусть ф-ия z=f(x,y) определена и непрерывна и имеет непрерывгные частные производные 1ого, 2ого порядков в окрестности критической точки М₀(х₀,у₀), в которой f’_х(х₀,у₀)=0 и f’_у(х₀,у₀)=0. Тогда:

1.если определитель

Δ=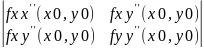 =f_xx’’(x₀,y₀)*f_yy’’(x₀,y₀)-(f_xy’’(x₀,y₀))²>0 и f_xx’(x₀,y₀)>0, то в точке М₀-ф-ия имеет минимум.

2.Если Δ<0 и f_xx’(x₀,y₀)<0, то в точке М₀-ф-ия имеет максимум.

3.если Δ<0, то ф-ия не имеет экстремума в точке М_0.

4.если Δ=0, то экстремум в точке М₀ мб и м не б. В этом случае требуется дальнейшее исследование.