Билет №3

1.Дифференциируемость и дифференциал функции двух переменных. Необходимые условия дифференцируемости. (Доказать)

Опр: ф-ия Z=f(x,y) называется дифференцируемой в точке М₀(х₀,у₀), если ее полное приращение в этой точке может быть представлено в виде: ΔZ=A₁ +A₂Δy+α(Δx,Δy)Δx+β(Δx,Δy)Δy (1), где A₁ A₂ – некоторые числа, не зависящие от Δx и Δy, α(Δx,Δy) и β(Δx,Δy) – бесконечно малые ф-ии при Δx→0, Δy→0.

Условие дифференцируемости (1) можно записать: ΔZ=A₁Δx+A₂Δy+0(р) (2).

Если хотя бы одно из чисел A₁ A₂ отлично от 0, то сумма A₁Δx+A₂Δy представляет собой главную, линейную относительно Δx и Δy часть приращения ф-ии в точке М₀(х₀,у₀). Ее называют дифференциалом ф-ии Z=f(x,y) в точке М₀(х₀,у₀) и обозначают dz или df.

Т.Необходимые условия дифференцируемости. Если ф-ия Z=f(x,y) дифференцируема в точке М₀(х₀,у₀), то:

1.Ф-ия непрерывна в этой точке

2.Сущ-ют в этой точке частные производные df/dx и df/dy, причем A₁=df/dx, A₂=df/dy.

Док-во:

1.Из условия дифференцируемости Ф-Ии в данной точке следует, что 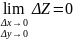, а это означает, что ф-ия непрерывна в точке М₀(х₀,у₀).

2.Из условия (1) частное приращение ф-ии по х в точке М₀ равно Δ_xZ= A₁Δx+αΔx. Тогда Δ_xZ/Δx=A₁+α, а , т.к. α→0 при Δx→0, Δy→0. Аналогично А₂=df/dy.

Следствие: условие дифференцируемости ф-ии в данной точке М₀ можно записать в виде: ΔZ=df(х₀,у₀)/dx Δx+ df(х₀,у₀)/dy Δy+0(р) или ΔZ=dZ+0(р), где dZ= df(х₀,у₀)/dx Δx+ df(х₀,у₀)/dy Δy.

Билет №4

1.Теорема о достаточных условиях дифференцируемости функции двух переменных. (Доказать)

Пусть ф-ия Z=f(x,y) имеет в окрестности точки М₀(х₀,у₀) частные производные df/dx и df/dy причем эти частные производные непрерывны в точке М₀. Тогда ф-ия Z=f(x,y) дифференцируема в точке М₀(х₀,у₀).

Док-во:

Дадим независимым переменным приращения Δx и Δy такие, чтобы точка М₀(х₀+Δx,у₀+Δу) U(М₀). Полное приращение ф-ии ΔZ=f(х₀+Δx,у₀+Δу)-f(х₀,у₀) представим в виде ΔZ=[f(х₀+Δx,у₀+Δу)- f(х₀,у₀+Δу)]+[f(х₀,у₀+Δу)-f(х₀,у₀)] (1).

Выражение [f(х₀+Δx,у₀+Δу)- f(х₀,у₀+Δу)] стоящее в первой квадратной скобке, можно рассматривать как приращение ф-ии f(х₀,у₀+Δу) одного переменного х на отрезке [х₀,х₀+Δx] (значение не меняется). По условию, ф-ия Z=f(x,y) имеет частные производные в U(М₀), поэтому ф-ия f(х₀,у₀+Δу) имеет производную по х, равную df/dx.

Применим теорему Лагранжа (f’(c)=f(b)-f(a)/b-a) к ф-ии f(х₀,у₀+Δу) на отрезке [х₀,х₀+Δx]:

f(х₀+Δx,у₀+Δу)-f(х₀,у₀+Δу)=Δx df/dx( ,у₀+Δу) (2) где х₀< <х₀+Δx.

Аналогично получим f(х₀,у₀+Δу)-f(х₀,у₀)=Δу df/dy(х₀, ) (3) где у₀< <у₀+Δу. Подставляя выражения 3 и 2 в равенство 1, получим ΔZ=Δx df/dx( ,у₀+Δу)+ Δу df/dy(х₀, ) (4).

Т.к., по условию теоремы, частные производные непрерывны в т.М₀, то

,у₀+Δу)/dx=df(х₀,у₀)/dx фигскобка

= df(х₀,у₀)/dy (5)

( →х₀, →у₀ при Δx→0, Δy→0). Из равенств 5 следует:

df( ,у₀+Δу)/dx=df(х₀,у₀)/dx+α фигскобка

df(х₀, )/dy= df(х₀,у₀)/dу+β (6)

С учетом 6, выражение 4 запишем в виде ΔZ= df(х₀,у₀)/dx Δx+ df(х₀,у₀)/dу Δу+αΔx+βΔу (7)

Следовательно, ф-ия Z=f(x,y) дифференцируема в т.М₀.

Замечание:будем называть приращения независимых переменных Δx и Δу дифференциалами независимых переменных и обозначать dx dy соответственно.

Тогда дифференциал ф-ии в т.М₀ записывается в виде: ΔZ= df(х₀,у₀)/dx dx+ df(х₀,у₀)/dу dy.