Билет №31

1.Способ неопределенных коэффициентов для нахождения частного решения линейного дифференциального уравнения 2-ого порядка с постоянными коэффициентами.

Рассмотрим неоднородное линейное ур-е 2-ого порядка с постоянными коэффициентами y’’+py’+qy=f(x) (1) где p, q – постоянные числа. f(x)-непрерывна на (a,b).

Для некоторых частных видов правой части (1) - f(x) удается найти частное решение ур-я способом неопределенных коэффициентов.

Частное решение ур-я ищется в форме аналогичной форме правой части ур-я, форма уточняется с тем, какие корни характеристического ур-ия.

1.f(x)=P_m(x)e^ax, P_m-алгебраический многочлен степени m.

1)Число а не является корнем характеристического ур-я x²+px+q=0.

y₁=Q_m(x) e^ax, Q_m(x)=A₀+A₁x+A₂x²+…+A_mx^m, A₀, A₁- неизвестные коэффициенты, можно найти способом неопределенных коэффициентов.

2)Число а – простой корень харак ур-я: y₁=хQ_m(x) e^ax,

3)Число а –двукр корень: y₂=х²Q_m(x) e^ax.

2. f(x)=Mcosbx+Nsinbx i=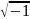

1) Число bi не явл корнем хар ур-я x²+px+q=0. у=Acosbx+Bsinbx

2) Число bi явл корнем хар ур-я x²+px+q=0. y=x(Acosbx+Bsinbx)

3.f(x)=p(x) e^axcosbx+q(x) e^axsinbx

1)a+bi не явл корнем хар ур-я x²+px+q=0. y=U(x) e^axcosbx+V(x) e^axsinbx

2) a+bi явл корнем хар ур-я x²+px+q=0. y=x[U(x)e^axcosbx + V(x)e^axsinbx]

В случаях 2 и 3 форма отыскания частного решения сохраняется и тогда правая часть ур-я (1) содержит только cosbx или sinbx.