Билет №24
1.Дифференциальные уравнения, допускающие понижение порядка.
1.Ур-я вида y(n)=f(x) (1). Этот тип ур-й играет важную роль, потому что к нему сводятся ур-я других видов.
Порядок ур-я понижается путем последовательного интегрирования.
Т.к. y(n)=(y(n-1))’, то ур-е y(n)=f(x) можно переписать так: (y(n-1))’=f(x), откуда y(n-1)= +C1.
Интегрируя
еще раз: y(n-2)=∫(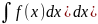
+C1x+C2.
Продолжая далее, после n интегрирований получим общее решение ур-я (1): у=∫dx∫dx… +C1x(n-1)+C2x(n-2)…+Cn-1x+Cn
2.Ур-я вида y’’=f(x,y’) не содержащие явно искомой ф-ии у. Это позволяет понизить порядок ур-я при помощи подстановки y’=p(x). Тогда y’’=p’(x). Подставив выражение производных в ур-е y’’=f(x,y’), получим ур-е первого порядка относительно неизвестной ф-ии р(х): p’=f(x,p). Проинтегрировав это ур-е, найдем его общее решение p=p(x,C1), а затем общее решение ур-я: у=∫p(x,C1)dx+C2.
Замечание:
аналогично интегрируя ур-е вида
y(n)=f(y(n-1)).
Полагая y(n-1)=р,
получим для определения р ур-е 1ого
порядка p’=f(p),
откуда
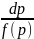=dx,
р=р(х,С1) или y(n-1)=р(х,С1).
Это ур-е вида y(n)=f(x).
Билет №25
1.Линейные дифференциальные уравнения высших порядков. Теорема Пикара о существовании и единственности решения (не доказывать). Линейный дифференциальный оператор, его свойства. Теорема о свойствах частных решений линейного однородного уравнения (доказать).
Линейным диф ур-ем n-ного порядка называется ур-е вида:
y(n)+p1(x)y(n-1)+p2(x)y(n-2)+…+p(n-1)(x)y’+p(n)(x)y=f(x) (1)
Теорема Пикара о существовании и единственности решения для линейного ур-я: если в ур-ии (1) все коэффициенты ур-я p1(x), p2(x), …, p(n)(x) и правая часть f(x) непрерывны в интервале (a,b), то оно имеет единственное решение у=ф(х), удовлетворяющее начальным условиям: у=у0, y’=y’0, …, y(n-1)=y0 (n-1) при х=х0, где х0 (a,b), а у0, y’0,…, y0 (n-1)-любые заданные числа. Это решение определено и n раз дифференцируемо во всем интервале (a,b).
Если в (1) правая часть f(x) тождественно равна 0 в интервале (a,b), то ур-е (1) принимает вид: y(n)+p1(x)y(n-1)+p2(x)y(n-2)+…+p(n-1)(x)y’+p(n)(x)y=0 (2) и называется линейным однородным ур-ем.
Если f(x)≠0 в интервале (a,b), то ур-е (1) называется линейным неоднородным ур-ем.
Для сокращения записи введем линейный дифференциальный оператор:
L(y)= y(n)+p1(x)y(n-1)+p2(x)y(n-2)+…+p(n-1)(x)y’+p(n)(x)y (3)
L – ставит в соответствие каждой ф-ии у(х) новую ф-ию L(y).
Оператор L(y) обладает след осн св-ми:
1.Постоянный множитель можно выносить за знак оператора: L(Cy)=CL(y)-св-во однородности.
2.Оператор от суммы 2ух ф-ий равен сумме операторов от этих ф-ий: L(y1+y2)=L(y1)+L(y2)-св-во аддитивности.
Теорема о св-ах частных решений линейного однородного ур-я.
Т1: если ф-ия у1 есть решение линейного однородного ур-я (2), т.е. L(y1)Ξ0, то ф-ия Сy1, где С-произвольная постоянная, тоже является решением этого ур-я.
Док-во:
По св-ву однородности линейного оператора: L(Cy1)=CL(y1). Но по условию теоремы, L(y1)Ξ0, поэтому CL(y1)Ξ0, а это и означает, что Cy1 есть решение ур-я (2).
Т2: если ф-ии у1 и у2 – решения ур-я (2), то их сумма у= у1+ у2 тоже является решением ур-я (2).
Док-во:
По св-ву аддитивности оператора L(y1+y2)=L(y1)+L(y2). По условию теоремы L(y1)Ξ0, L(y2)Ξ0. Поэтому L(y1+y2)Ξ0, т.е. ф-ия у= у1+ у2 –решение ур-я (2).
Т3: если ф-ии у1, у2,…,уn- решения ур-я (2), то их линейная комбинация у=С1у1+С2у2+…+Cnyn, где С1,С2,…,Сn – произвольные постоянные, тоже являются решением ур-я (2).
Док-во:
По Т1 каждая из ф-ий С1у1, С2у2, …, Cnyn является решением ур-я (2).
По Т2 ф-ия 1= С1у1+С2у2 есть решение ур-я (2), ф-ия 2= 1+ С3у3-решение ур-я (2) и тд.