Билет №8
1.Скалярное поле. Производная по направлению: определение, формула для вычисления (доказать). Градиент: определение, его связь с производной по направлению (доказать формулу).
Пусть ф-ия U=f(x,y,z) задана в некоторой пространственной обл V. (x,y,z) V. В этом случае задано скалярное поле в обл V.
Пример: Если в каждой точке некоторого объема известно давление газа, задано поле давления газа.
Производная по направлению: в обл V задано скалярное поле. Пусть М0(х0,у0,z0) V.М1(х0+Δх,у0+Δу,z0+Δz).
ΔS=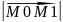
=
,
ΔU=U(M1)-U(M0)
Опред: если
сущ-ет lim отношения:
,
то он называется производной по
направлению ф-ии U в т.S
по направлению ΔS.
δU/δS>0, то U↑ в т. M0,
δU/δS<0, то U↓ в т. M0.
Градиент: в
обл V задано скалярное
поле и в каждой точке поля определен
вектор
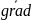U=δU/δx
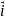+δU/δy
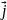+δU/δz
(частные
производные в данной точке)
Теорема:
δU/δS=пр.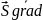
U=
cosφ
(φ=(.
,
U)),
ф-ия дифференцируема в обл V.
1.Производная по направлению в данной точке есть:
δU/δS= δU/δx cosα+δU/δy cosβ+δU/δz cosγ (1)
(αβγ)-углы с осями координат
т.к. U(x,y,z) дифференцируема в обл V, то ее приращение можно записать:
ΔU= δU/δxΔх+δU/δyΔу+δU/δzΔz+о(ΔS) (2)
Поделим левую,правую части на ΔS:
ΔU/ΔS= δU/δx Δх/ΔS +δU/δy Δу/ΔS+δU/δz Δz/ΔS+о(ΔS)/ΔS (3)
Δх/ΔS=cosα, Δу/ΔS=cosβ, Δz/ΔScosγ – направляющие косинусы вектора
В равенстве (3) переходим к пределу при ΔS→0.
δU/δS|М0= δU/δx|М0cosα+δU/δy|М0cosβ+δU/δz|М0cosγ
Док-во:
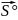(орт-вектора S)=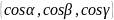
Подсчитаем скалярное произведение:
U = δU/δx cosα+δU/δy cosβ+δU/δz cosγ – производная по направлению в данной точке δU/δS|М0.
U
=
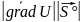cosφ=
cosφ=
пр.
U
(4),чтд
Из формулы (4): δU/δS= пр. U= cosφ (5)
Следствие из теоремы: cosφ=1, δU/δS= -самое большое значение (φ=0)
Билет №9
1.Неявная функция. Определение, примеры. Теорема о существовании и дифференцируемости неявной функции (сформулировать).
Ф-ия у=f(x) называется неявной,если она задана с помощью ур-я F(x,y)=0, не разрешенного относительно у.
Пример: F(x,y)=х2+у2-1
Теорема о существовании и дифференцируемости неявной ф-ии: Пусть F(x,y), (x,y) U(х0,у0) и выполняются условия:
1. F(x,y), F’x, F’у-непрерывны в U(х0,у0)
2. F(х0,у0)=0
3. F’у(х0,у0)≠0
Тогда: прямоугольная окрестность (х0,у0).
П(х0,у0)=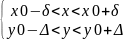
,
в которой F(x,y)=0
определяет у=f(x),
х
(х0-δ,х0+δ).
Эта ф-ия непрерывна и имеет непрерывную
производную y’=f’(x)=
-F’x/F’у,
х
(х0-δ,х0+δ).
Билет №10
1.Первообразная и неопределенный интеграл (определения). Свойства неопределенного интеграла. Таблица основных интегралов.
Опред1: ф-ия F(x) называется первообразной для f(x) на Х, если сущ-ет F’(x),х Х и F’(x)=f(x).
Опред2:
совокупность всех первообразных ф-ий
для данной ф-ии f(x),х
Х
называется неопределенным интегралом
от ф-ии f(x)
и обозначается
=F(x)+C,
F’(x)=f(x).
Интегрирование – отыскание для f(x) всех первообразных.
Основные св-ва неопределенного интеграла:
1.( )’=(F(x)+C)’=F’(x)=f(x)
2.d( )=d(F(x)+C)=dF(x)=F’(x)dx=f(x)dx
3.
=
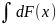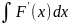=F(x)+C
Св-ва линейности:
1.
=
±
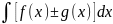2.
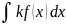=k
Таблица основных интегралов:
1.
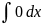=C
2.
=x+C
3.
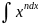=xn+1/n+1+C
4.
=ln|x|+C
5.
=ax/lna+C
5’.
=ex+C
6.
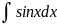=-cosx+C
7.
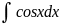=sinx+C
8.
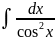=tgx+C
9.
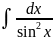=-ctgx+C
10.
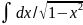=arcsinx+C
10’.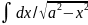
=arcsin
x/a+C
11.
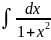=arctgx+C
11’.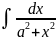
=1/a
arctg x/a+C
12.
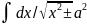=ln|x+
|+C
13.
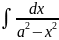=1/2a
ln
+C