Билет №14

1.Вычисление ∫R(Sinx,Cosx)dx (1). Универсальная и частная замены. Вычисление ∫Sin^mxCosⁿx dx. Тригонометрические замены.

Подынтегральная ф-ия-рациональная ф-ия, аргументами которой являются sinx, cosx. Этот интеграл при помощи универсальной замены t=tg x/2 приводится к интегралу от рац ф-ии переменной t, т.к. sinx, cosx, dx рац выражаются через t=tg x/2.

Sinx=(2tgx/2)/(1+tg²x/2)=2t/(1+t²), cosx=(1-tg²x/2)/(1+tg²x/2)=(1-t²)/(1+t²), x/2=arctgt, dx=2dt/(1+t²)

Т.к. рациональная ф-ия от рациональных ф-ий есть ф-ия рациональная, то подставив эти выражения (1), получим интеграл от рациональных ф-ий.

=

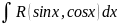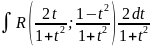
Универсальная замена t=tg x/2 позволяет проинтегрировать любую ф-ию R(Sinx,Cosx), однако может привести к трудоёмким вычислениям.

Если выполняется условие R(-sinx;-cosx)=R(sinx;cosx), т.е. sinx, cosx входят под знак интеграла только в четных степенях, то удобнее применять частную подстановку t=tgx. При этом:

Cos²x=1/(1+tg²x)=1/(1+t²), sin²x=tg²x/(1+tg²x)=t²/(1+t²), x=arctgx, dx=dt/(1+t²), т.е. Cos²x, sin²x, dx выражаются рационально через t. Поэтому выполнив замену переменной t=tgx, получим интеграл от рациональной ф-ии переменной t.

К интегралу вида (1) относится также ∫Sin^mxCosⁿx dx, просто этот ∫ вычисляется в след случаях:

1.либо m либо n – нечетное число. (n-нечетное: t=sinx; m: t=cosx)

2.(m+n) – чётное отрицательное число: t=tgx

3. m и n – чётные числа, используем формулы понижения степени: cos²x=(1+cos2x)/2, sin²x=(1-cos2x)/2.

Тригонометрические замены: к интегралу вида ∫R(Sinx,Cosx)dx приводятся интегралы:

∫R(x,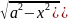 dx при помощи замены х=asint

∫R(x, dx при помощи замены х=atgt

∫R(x, dx при помощи замены х=a/sint

Билет №15

1.Определенный интеграл. Определение, геометрический смысл.

Пусть на отрезке [a,b] задана ф-ия у=f(x). Произвольно выберем на отрезке [a,b] точки

а=х₀,х₁,х_i-1,x_i,…,х_n=b. Такой набор точек x_i, i=1,2,..,n будем называть разбиением отрезка [a,b] и обозначать Т. Обозначим Δx_i= x_i - х_i-1 – длина отрезка. [х_i-1, x_i]; λ=maxΔx_i, 1≤i≤n, будем называть параметром разбиения. В каждом из отрезков [х_i-1, x_i] произвольно выберем т.с_i. Набор точек {с_i}={c₁,c₂,…,c_n} будем называть промежуточными точками. Составим сумму: f(c₁)Δx₁+ f(c₂)Δx₂+…+ f(c_n)Δx_n= =σ (1). Эта сумма – интегральная сумма для ф-ии f(x) на отрезке [a,b], соответствующая данному разбиению Т отрезка [a,b] и данному набору промежуточных точек {с_i}.

Опред1: Число J называется пределом интегральной суммы при λ→0: J=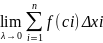 , если ε>0 δ>0 такое, что 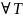с λ(Т)<δ и 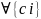(независимо от набора промежуточных точек) выполняется неравенство <ε.

Опред2: ф-ия f(x) называется интегрируемой на отрезке [a,b], если сущ-ет = J. Величина этого предела называется определенным интегралом от данной ф-ии по данному отрезку и обозначается 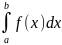. Числа а и в называются соответственно нижним и верхним пределом интеграла, х – переменной интегрирования. Определенный интеграл(число) не зависит от того, какая стоит переменная под интегралом, ее можно обозначить любой буквой =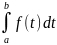 , а зависит только от ф-ии f(x) и отрезка [a,b].

Т о сущ-нии определенного интеграла: если ф-ия f(x)непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.

Геометрический смысл определенного интеграла: пусть f(x)≥0, х [a,b]. Тогда число равно площади прямоугольника с основанием Δx_i= x_i - х_i-1 и высотой f(c_i). Следовательно интегральная сумма равна площади ступенчатой фигуры, образованной из прямоугольников с основаниями и высотами соответсвенно: .

Площадь этой ступенчатой фигуры σ≈S – площадь криволинейной трапеции- фигуры, ограниченной графиком ф-ии у= f(x), 2умя прямыми х=а и х=в и отрезком[a,b] оси 0х. Т.о. σ= ≈S.

Погрешность этого равенства будет тем меньше, чем меньше длина каждого отрезка разбиения , т.е. чем меньше λ. Точное значение площади криволинейной трапеции: S= = .