Билет №26
1.Понятие о линейной независимости функций. Определитель Вронского для функций. Теорема о необходимом условии линейной зависимости двух функций (доказать).
Набор чисел С1,С2,…,Сn –будем называть тривиальным, если все эти числа равны 0.
Набор чисел С1,С2,…,Сn –будем называть нетривиальным, если хотя бы одно из этих чисел Сi≠0, 1≤i≤n.
Линейную комбинацию ф-ий С1у1+С2у2+…+Cnyn будем называть тривиальной, если набор чисел С1,С2,…,Сn – тривиальный; нетривиальной, если набор чисел С1,С2,…,Сn –нетривиальный. Пусть ф-ии у1, у2…уn определены и непрерывны на интервале (a,b).
Опред1: ф-ии у1, у2…уn называются линейно зависимыми на интервале (a,b), если сущ-ет их нетривиальная линейная комбинация, равная 0 для всех х (a,b), т.е. С1у1+С2у2+…+Cnyn=0 х (a,b), если Сi≠0, 1≤i≤n.
Опред2: ф-ии у1, у2…уn называются линейно независимыми на интервале (a,b), если только их тривиальная линейная комбинация равна 0 для всех х (a,b), т.е. С1у1+С2у2+…+Cnyn=0 х (a,b) ↔ Сi=0 i, 1≤i≤n.
Если одна из ф-ий у1, у2…уn тождественно равна 0 на интервале (a,b), то эти ф-ии динейно зависимы на (a,b).
Пусть ф-ии у1, у2 имеют производные порядка n-1. Определитель n-ного порядка
w(x)=
называется определителем Вронского для ф-ий у1, у2 или вронскианом этих ф-ий.
Т1.Если ф-ии у1, у2 линейно зависимы на (a,b),то их определитель Вронского w(x)=0 в каждой точке интервала.
Док-во:
По условию у1(х) и у2(х)-линейно зависимые на (a,b).
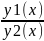=λ ,
х
(a,b),
где λ-число.
у1(х)=λ у2(х)
у’1(х)=λ у’2(х)
Составим определитель Вронского:
W(x)=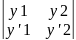
=
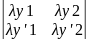=λy1y’2-λy2y’1=0,
чтд
Билет №27
1.Необходмое и достаточное условие линейной независимости двух решений однородного линейного дифференциального уравнения второго порядка.
Т2 о необходимом условии линейной зависимости 2ух ф-ий:
Если ф-ии у1, у2 – линейно независимое решение линейного ур-я 2ого порядка y’’+p1(x)y’+p2(x)y=0, коэффициенты которого p1(x) и p2(x) – непрерывные ф-ии на (a,b), то w(x)≠0 х (a,b).
Док-во: от противного. х0 (a,b), w(x0)=0.
Обозначим: у1(х0)=(у1)0, у2(х0)=(у2)0, у’1(х0)=(у’1)0, у’2(х0)=(у’2)0 . Рассмотрим систему 2ух однородных ур-ий относительно неизвестных С1 и С2.
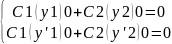
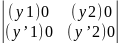=w(x0)=0
В курсе алгебры доказано, что если определитель однород системы линейных ур-й равен 0, то система имеет нетривиальные решения.
Пусть С1=α1, С2=α2 – нетривиальное(ненулевое) решение системы.
Рассмотрим у= α1у1+ α2у2. Согласно Т3 о св-ах решений линейных однород ур-й, эта ф-ия – есть решение ур-я y’’+p1(x)y’+p2(x)y=0.
у(х0)= α1у1(х0)+ α2у2(х0)= α1(у1)0+ α2(у2)0=0.
у’(х0)= α1у’1(х0)+ α2у’2(х0)= α1(у’1)0+ α2(у’2)0=0.
Ф-ия у= α1у1+ α2у2 – решение ур-я y’’+p1(x)y’+p2(x)y=0, которое удовлетворяет системе начальных условий.
Нулевая система: у(х0)=0, y’(x0)=0. y’’+p1(x)y’+p2(x)y=0 имеет очевидное решение у(х)=0 при той же системе нулевых условий.
По т.Пикара о сущ-ии и единственности решения линейного ур-ия: на (a,b) сущ-ет только одно решение ур-я y’’+p1(x)y’+p2(x)y=0→ у= α1у1+ α2у2=0 х (a,b) при этом α1 и α2 - нетривиальная→ у1, у2 –линейно зависимы на (a,b), что противоречит условию.
Следствие из Т1 и Т2: 2 решения ур-я y’’+p1(x)y’+p2(x)y=0 у1(х) и у2(х)- линейно независимы на (a,b) тогда и только тогда, когда их w(x)≠0 х (a,b).
Док-во: если у1(х) и у2(х)-лин.независимые решения, то w(x)≠0 х (a,b) (Т2)
Обратно: пусть w(x)≠0 х (a,b). Противное: у1(х) и у2(х)-линейно зависимые→Т1 w(x)=0, противоречие.