Билет №22

1.Дифференциальные уравнения первого порядка с однородными функциями. Определение, их решения.

Опред1: ф-ия f(x,y) называется однородной n-ого измерения относительно х и у, если при любом t справедливо: f(tx,ty)=tⁿf(x,y).

Опред2: ур-е P(x,y)dx+Q(x,y)dy=0 (1) называется ур-ем с однородными ф-ми, если P(x,y) и Q(x,y)-однородные относительно х и у одного и того же измерения.

Утверждение: ур-е с однородными ф-ми мб приведено к виду: y’=φ(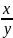 ) (2).

Док-во:

Пусть P(x,y) и Q(x,y)-однородные ф-ии измерения n, т.е. Р(tx,ty)= tⁿР(x,y), Q(tx,ty)= tⁿQ(x,y).

Умножим обе части ур-я (1) на tⁿ: tⁿP(x,y)dx+ tⁿQ(x,y)dy=0 или Р(tx,ty)dx+Q(tx,ty)dy=0.

Возьмем t=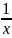 . Р(1,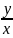 )dx+Q(1, )dy=0. Перепишем это ур-е в форме, разрешенной относительно производной: 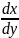=- 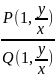. Первая часть ур-я есть ф-ия отношения , т.е. мы пришли к ур-ю вида (2).

Ур-я с однородными ф-ми решают при помощи подстановки u= (3), которая преобразует это ур-е в ур-е с разделяющимися переменными относительно новой искомой ф-ии u(x).

Из равенства (3) найдем у=ux, y’=u+u’x и подставим в ур-е (2). Получим u+u’x=f(u).

Перепишем ур-е в дифференциалах, заменив u’=du/dx.

Придем к ур-ю с разделяющими переменными xdu+(u-f(u))dx=0. Разделим обе части ур-я на x(u-f(u)):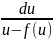 + 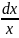=0, откуда 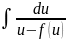+ln|x|=ln|C₁|.Обозначим - =Ф(u). Тогда Ф(u)= ln|х/C₁|;

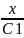=е^Ф(u).

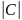= е^Ф(u) и х=Се^Ф(u)(С=± ).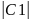

Общий интеграл ур-я y’=φ( ) примет вид х=Се^{Ф( ).}

Замечание: мы делим обе части ур-я xdu+(u-f(u))dx=0 на x(u-f(u)). Поэтому это ур-е может иметь особые решения вида u=a, где а-корень ур-я u-f(u)=0, а также х=0.Тогда исходное ур-е y’=φ( ) может иметь особые решения: у=ах(х≠0) и х=0(у≠0)

Билет №23

1.Линейные дифференциальные уравнения первого порядка. Решение методом вариации произвольного постоянного.

Диф ур-е 1ого порядка называется линейным, если оно содержит искомую ф-ию у и ее производную y’ только в первой степени. Общий вид линейного ур-я 1ого порядка y’+P(x)y=Q(x) (1) где P(x) и Q(x) – заданные непрерывные ф-ии от х(или постоянные).

Если правая часть ур-я Q(x)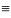 0, то ур-е (1) называется линейным однородным, если Q(x)≠0, это ур-е линейное неоднородное.

Решение линейного ур-я способом вариации произвольного постоянного.

Для линейного ур-я y’+P(x)y=Q(x) запишем соответствующее ему однородное уравнение ур-е 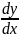+P(x)y=0 (2). Оно является ур-м с разделяющимися переменными 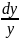+P(x)dx=0, откуда

ln =- +ln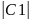 , =e^- +ln =|C₁|e^-∫P(x)dx и у=±|C₁|e^-∫P(x)dx.

Обозначив ±|C₁|=С получим общее решение ур-я (2) у=Сe^-∫P(x)dx (3).

Будем искать решение неоднородного ур-я (1) в том же виде (3), что и решение однородного ур-я (2), но С будем рассматривать как некоторую диф ф-ю от х, т.е. положим у=С(х)e^-∫P(x)dx (4) и подберем ф-ю С(х) так, чтобы ф-ия (4) стала решением неоднородного ур-я (1).

Для этого подсчитаем: y’=C’(x)e ^-∫P(x)dx+C(x)e ^-∫P(x)dx(-P(x)). (5)

Подставим в ур-е (1) у согласно (4) и y’ согласно (5) и потребуем, чтобы оно обратилось в тождество:

C’(x)e ^-∫P(x)dx-P(x)C(xe ^-∫P(x)dx+P(x)C(x)e ^-∫P(x)dx=Q(x)

Два средних члена взаимно уничтожаются и ур-е y’+P(x)y=Q(x) переходит в ур-е с разделяющимися переменными относительно ф-ии С(х).

C’(x)=Q(x) e ^∫P(x)dx (6)

Общее решение ур-я (6): C(x)=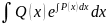 +C₁, где C₁(х)-произвольная постоянная.

Подставив найденное выражение С(х) в равенство у=С(х)e^-∫P(x)dx, получим решение неоднородного ур-я (1): у=[ +C₁]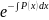 .