Билет №16

1.Свойства определенного интеграла (перечислить, теорему о среднем доказать).

1.Пусть f(x), g(x) интегрируемы на отрезке [a,b]. Тогда ф-ии f(x)±g(x) также интегрируемы на отрезке [a,b], причем = +

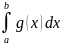
2.Пусть f(x) интегрируема на [a,b]. С-число. Тогда С*f(x) интегрируема на [a,b], причем

=C .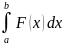

3.Пусть ф-ия f(x) интегрируема на отрезках [a,c] и [с,b], a<c<b. Тогда f(x) интегрируема на [a,b], причем = +

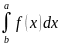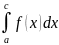4. Пусть f(x), φ(x) интегрируемы на отрезке [a,b] и удовлетворяют условию f(x)≤φ(x). Тогда ≤

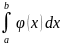
5. Пусть f(x) интегрируема на [a,b].m и M-наименьшее и наибольшее значения ф-ии на отрезке. Тогда m(b-a)≤ ≤M(b-a)

6. Теорема о среднем.

Пусть f(x) непрерывна на отрезке [a,b]. Тогда на этом отрезке найдется точка С, такая, что =f(C)(b-a)

Док-во:

Пусть m и M-наименьшее и наибольшее значения ф-ии на отрезке [a,b], существующие по первой теореме Вейерштрасса.

По св-ву 5: m≤ ≤M. Обозначим =μ.

Т.к. f(x) непрерывна на отрезке [a,b], то по второй теореме Больцано-Коши, она принимает промежуточное значение μ в некоторой точке С отрезка[a,b], т.е. найдется точка С [a,b] такая, что

μ=f(C), т.е. f(C)= или =f(C)(b-a).

Билет №17

1.Определенный интеграл с переменным верхним пределом. Определение. Теорема об его производной (доказать). Формула Ньютона-Лейбница (доказать).

Пусть ф-ия f(t) интегрируема на отрезке [a,b]. Возьмем х [a,b]. По св-ву 3(Пусть ф-ия f(t) интегрируема на отрезках [a,c] и [с,b], a<c<b. Тогда f(x) интегрируема на [a,b], причем = + ) f(t) интегрируема и на отрезке [a,x]. Подсчитаем . Это будет некоторое число равное площади криволинейной трапеции аАХх. Т.о. х [a,b] ставится в соответствие число . Тем самым на отрезке [a,b] задана ф-ия F(x)= , которую называют определенным интегралом с переменным верхним пределом.

Теорема: пусть ф-ия f(t) непрерывна на отрезке [a,b]. Тогда ф-ия F(x) имеет производную в каждой точке х [a,b], причем

F’(x)=( )=f(x).

Док-во:

Дадим аргументу приращение Δх и подсчитаем приращение ф-ии ΔF.

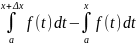ΔF=F(x+Δх)-F(x)= - =(по св-ву 3) + = =(по св-ву 6.Теорема о среднем.Пусть f(x) непрерывна на отрезке [a,b]. Тогда на этом отрезке найдется точка С, такая, что =f(C)(b-a)) …=f(c)Δx, x<C<x+Δх.

Составим разностное отношение: 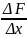= =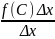f(C).

Тогда F’(x)=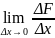 = =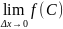 =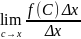f(x) (c→x в силу непрерывности f(x) на [a,b]).

Т.о. мы доказали утверждение, о том, что для непрерывной на отрезке [a,b] ф-ии f(x) всегда сущ-ет первообразная, примером ее является определенный интеграл с переменным верхним пределом F(x)= .

Формула Ньютона-Лейбница: Пусть Ф(х)-какая либо первообразная для непрерывной ф-ии f(x) на отрезке [a,b]. Тогда справедлива формула: =Ф(b)-Ф(a)=Ф(х) .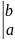

Док-во:

Для непрерывной на отрезке [a,b] ф-ии f(x) интеграл F(x)= является первообразной ф-ей. Было доказано ранее, что разность между 2умя первообразными равна постоянному числу:

F(x)-Ф(x)=C. Положим здесь х=а и учтем, что F(a)=0. Тогда 0-Ф(а)=С или С=-Ф(а). При х=b получим F(b)= =Ф(b)-Ф(a).

Билет №18

1.Замена переменной в определенном интеграле (доказать формулу). Интегрирование по частям.

, где f(x) непрерывна на отрезке [a,b]. Введем ф-ию х=φ(t):

1. φ(t) определена и непрерывна на [α;β]

2. [a,b]-множество значений ф-ии х=φ(t), когда t [α;β].

3.φ(α)=а; φ(β)=b

4. сущ-ет и непрерывна φ’(t) на [α;β].

Тогда справедлива формула = . (1)

Док-во:

Вычислим левый и правый интегралы формулы (1) исходя из какой либо первообразной для ф-ии f(x). Пусть Ф(x)-первообразная для ф-ии на отрезке [a,b].

Тогда левый интеграл (1) считаем по формуле Ньютона-Лейбница: =Ф(b)-Ф(a).

Рассмотрим сложную ф-ию Ф[φ(t)], t [α;β]. Эта сложная ф-ия дифференцируема на [α;β], т.к. ф-ии Ф(x) и φ(t) дифференцируемы на соответствующих отрезках [a,b] и [α;β].

По правилу отыскания производной сложной ф-ии:

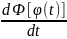=Ф’[φ(t)]*ф’(t)= ,поскольку x= φ(t)

Т.к. =f(x), при x= φ(t) получим Ф’[φ(t)]=f[φ(t)] и окончательно: = f[φ(t)]*ф’(t).

Следовательно ф-ия Ф[φ(t)] является первообразной для ф-ии f[φ(t)]*ф’(t) на отрезке [α;β](по определению первообразной).

По формуле Ньютона-Лейбница: =Ф[φ(β)]-Ф[φ(α)]=Ф(b)-Ф(a).

Левый и правый интегралы формулы (1) равны.

Замечание: при вычислении опр интеграла по формуле (1) нет надобности возвращаться к старой переменной. Если вычислен правый интеграл (1), то вычислен и левый.

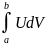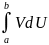Пусть ф-ии U(x), V(x) имеют непрерывные производные на [a,b]. Тогда =UV - -формула интегрирования по частям для определенных интегралов.