Міжгалузевий баланс

Модель базується на поняття «чиста галузь» (також на практиці використовують термін «вид економічної діяльності»), яка має такі ознаки:

1. Кожна галузь виробляє лише один продукт

2. Кожен продукт виробляється лише однією галуззю

3. Кожна галузь має єдину технологію.

Модель Леонтьєва

Щоб побудувати модель, припускаємо, що залежить від обсягу виробництва: .

Тобто кількість сировини виділеної на певний технологічний процес залежить від того скільки буде вироблятись? Хіба не мало б бути навпаки - ми спроможні виробити стільки, на скільки нам вистачить ресурсів? А скільки i-того ресурсу виділити кожній галузі буде залежати від того скільки її є ( )? Можливо, це пов'язано з тим, що виробництво працює на те, аби задовольнити попит, який загалом можна передбачити.

У найпростішій моделі припускають лінійну залежність між витратами та обсягом виробництва:

.

Коефіцієнт називається коефіцієнтом прямих виробничих витрат (технологічним коефіцієнтом) продукції i на виробництво продукції j.

Система рівнянь балансу приймає вигляд:

Тоді міжгалузевий баланс можна записати матричним рівнянням, яке і є моделлю Леонтьєва:

11.Лінійна модель міжнародної торгівлі

Розглянемо лінійну модель міжнародної торгівлі, яка приводить до поняття власного вектора і власного значення матриці.

Нехай є п країн S1, S2,..., Sn із національними доходами x1, x2,..., xn відповідно. Частку національного доходу, що країна Sj витрачає на за- купівлю товарів у країни Si, позначимо aij. Введемо структурну мат- рицю торгівлі A і вектор національних доходів країн X

Вважаємо, що весь національний дохід витрачається на закупів- лю товарів або всередині країни, або на імпорт з інших країн, тоді су- ма елементів будь-якого стовпця матриці А дорівнює 1

Для збалансованої торгівлі необхідна бездефіцитність торгівлі кожної країни Si, тобто виторг від торгівлі кожної країни повинний бути не менше її національного доходу

Нехай є n галузей промисловості, кожна з яких виробляє свою продукцію. Введемо позначення: − загальний обсяг продукції, що виготовляє і-та галузь (і=1,2,…,n) ; − обсяг продукції і-тої галузі, яку споживає j-та галузь (і, j = 1,2,…,n); − обсяг кінцевого попиту і-тої галузі.

Валовий обсяг і-тої галузі дорівнює галузі сумарному обсягу продукції, яку споживають n галузей, і кінцевій продукції, тобто 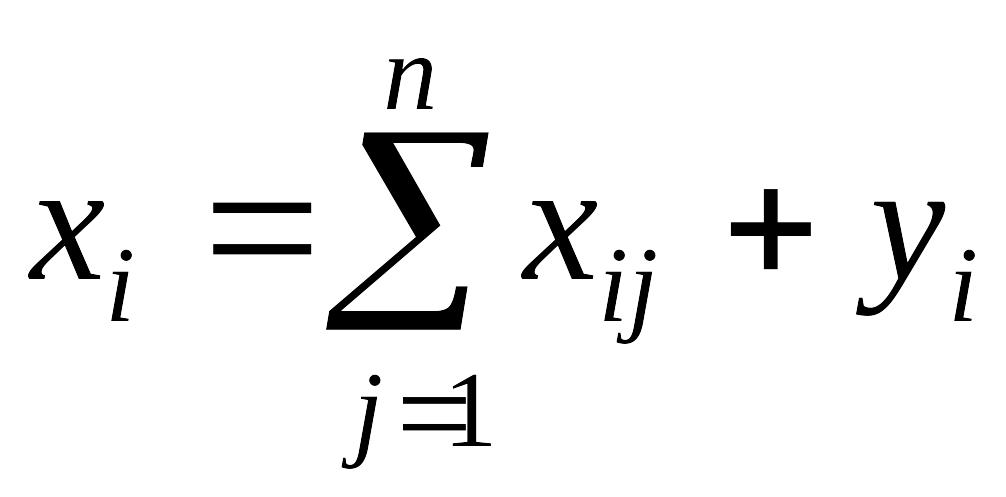. Останнє рівняння називаються співвідношеннями балансу. Це співвідношення можна записати у вигляді

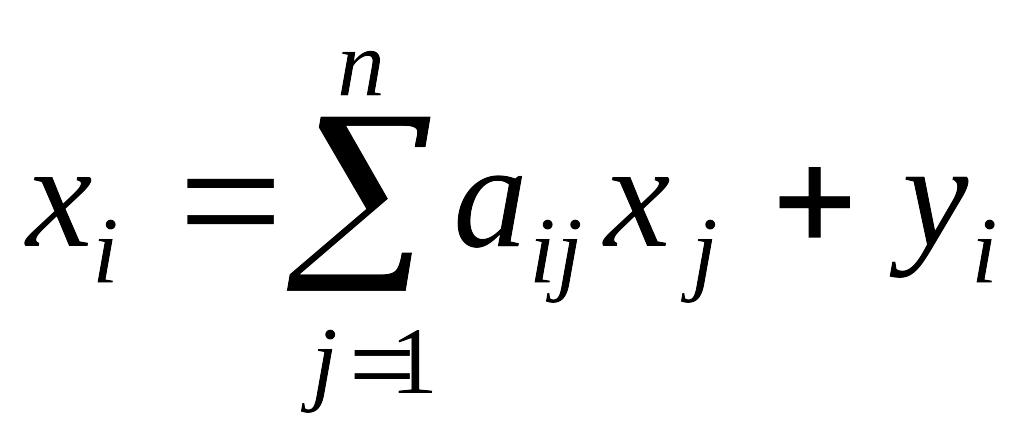(1)

де − коефіцієнти прямих витрат, які показують витрати продукції і-тої галузі на виготовлення одиниці продукції j-тої галузі.

Співвідношення балансу (1) можна записати у матричному вигляді

X=AX+Y, де

.

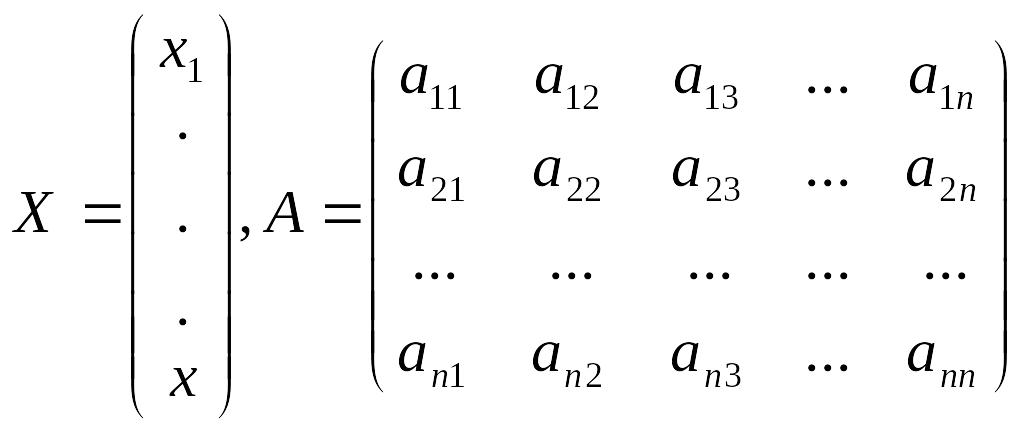Тут Х – матриця-стовпець валового випуску всіх видів продукції, А – матриця прямих витрат; Y – матриця-стовпець кінцевого попиту.

Основна задача міжгалузевого балансу складається в знаходженні такої матриці Х валової продукції, яка при відомій матриці А прямих витрат забезпечить задану матрицю Y кінцевої продукції.

Рівняння (2) можна переписати у вигляді

(Е-А)Х=Y (3)

Якщо матриця Е-А − невироджена, то маємо розв’язок системи (3)

. (4)

Матриця називається матрицею повних витрат.