Часть 2

22.Система мер Древней Руси. Пропорционирование при помощи косой и прямой сажени.

Система мер древней Руси У восточных славян, вполне возможно, были свои деревянные храмы и что они были многоголовыми. Многоглавие, таким образом, было исконно русской чертой зодчества, переняты вдальнейшем искусствоведами Киевской Руси. С христианством на Русь пришла крестово-купольная форма храмов, типичная для православных греко-восточных стран.

Крестово-купольный формы храмы, прямоугольные в плане, с 4 или более столбами, интерьер делится на продольные (по оси запад-восток) части - нефы (три, пять или более). Четыре центральных столба объединяются арками, которые поддерживают через паруса барабан купола. Пространство под куполом, благодаря окнам барабана, залито светом. Это центр храма. Алтарные помещения - апсиды располагаются на восточной стороне интерьера, обычно какими-то округлыми частями выступающие на внешней стороне; площадь в западной части обычно называют "притвором", "нартексом". В этой же части на втором ярусе размещены хоры, где были князь и его приближенные во время богослужения. Ячейки, которые примыкают к пространству под куполом, перекрыты сводами цилиндрической формы. Система мер древней Руси . Все пространство в центре храма в плане образует крест, откуда и пошло название системы подобного храма крестово-купольный. В домонгольском храме отличительной чертой было разделение фасада вертикальными плоскими пиастрами (по-древнерусски - лопатками) на "прясла". Овальное завершение прясла называется "закомарой" (их форма определяется посводным покрытием).  История искусства древней Руси.  В интерьере Древней Руси использовалась роспись стен насыщенных ярких цветов (синего, зелёного, красного... - "расписной терем"), болдахины на кроватях, витражи на окнах, своды на потолках, израсцовые печи... Искусство Киевской Руси имело огромное значение для дальнейшего развития художественной культуры русского народа и братских народов - белорусского и украинского. 

все 12 типоразмеров саженей: городовая 284,8 см, косая 248 см, великая 244,0 см, греческая 230,4 см, казенная 217,6 см, царская 197,4 см, церковная 186,4 см, народная 176,0 см, кладочная 159,7 см, простая 150,8 см, малая 142,4 смбез названия 134,5 см.

С помощью этого набора можно было не только разметить длины, но и все углы будущего строения. Например: соединив штырьками две «народных» и «косую» сажень, строитель получал прямой угол, «городовая», «малая» и «косая» давали прямоугольный треугольник с углами 90, 60 и 30 гр. Две «городовых» и «народная» – 1/10 окружности, две «городовых» и «царская» – 1/9 окружности, Две «городовых» и «казенная» – 1/8 окружности, две городовых и косая – 1/7 окружности. Хотите разделить окружность на 11 частей. Пожалуйста: для этого есть две «городовых» и «кладочная» сажень. Две «царских» и «греческая» дают 72 градуса, т.е. 1/5 окружности

Пропорционирование при помощи косой и прямой сажени. 

Пропорционирование — это использование пропорций для организации элементов формы в целостную структуру, то есть применение определенного метода количественного согласования частей и целого. Применение пропорций в архитектуре древнего мира было тесно связано с характером строительного производства и способами измерения. Необходимость нанесения контуров будущего здания на земле и вычерчивание его плана в натуральную величину способствовали развитию устойчивых приемов построения геометрических фигур и выработке определенных пропорциональных отношений для взаимосвязи их габаритов.

Одной из первоначальных задач, которая стояла перед строителями древности, являлось построение прямого угла и правильного прямоугольника. Древнерусские мастера, очевидно, пользовались при построении квадрата двумя взаимосвязанными мерами длины; простой саженью и косой. Величина косой сажени равнялась размеру диагонали квадрата со стороной, равной простой сажени. Такая взаимосвязь мер позволяла архитектору легко строить прямой угол с помощью плотничьего треугольника с двумя сторонами, равными простой сажени — 152,8 см и одной, равной косой сажени — 218 см. Для этого ему было достаточно сторону квадрата отложить в простых саженях, а его диагональ в косых, придерживаясь при этом одного и того же количества. Отношение стороны квадрата к его диагонали часто использовалось в пропорциональных построениях, так как позволяло легко образовать непрерывный ряд взаимосвязанных величин. Система вписанных или описанных квадратов была удобна, ибо давала зодчему своеобразную пропорциональную шкалу, на основании которой он мог строить соразмерность частей здания. Очень важно, чтобы система пропорционирования была единой для всего архитектурного организма, включая все его параметры и даже элементы внутреннего и внешнего благоустройства. В этом случае целостность восприятия сооружения усиливается, и оно приобретает художественную законченность.

23.Канон Поликлета и метод вращающихся квадратов.

Самое знаменитое произведение Поликлета — «Дорифор» (Копьеносец) (450—440 до н. э.). Считалось, что фигура создана на основе положений пифагореизма, поэтому в древности статую Дорифора часто называли «каноном Поликлета», тем более что «Каноном» назывался его несохранившийся трактат по эстетике. Здесь в основе ритмической композиции лежит принцип перекрестной неравномерности движения тела (правая сторона, то есть опорная нога и опущенная вдоль тела рука, статичны и напряжены, левая, то есть оставшаяся сзади нога и рука с копьем, расслаблены, но в движении). Формы этой статуи повторяются в большинстве произведений скульптора и его школы.

Расстояние от подбородка до темени в статуях Поликлета равняется одной седьмой от высоты тела, расстояние от глаз до подбородка — одной шестнадцатой, высота лица — одной десятой.

В своем «Каноне» Поликлет уделял большое внимание пифагорейской теории золотого деления (вся длина так относится к большей части, как большая к меньшей). Например, весь рост «Дорифора» относится к расстоянию от пола до пупка, как это последнее расстояние — к расстоянию от пупка до темени. При этом Поликлет отказывался от золотого деления, если оно противоречило естественным параметрам человеческого тела.

В трактате воплощаются также теоретические идеи о перекрещенном распределении напряжения в руках и ногах. «Дорифор» — ранний пример классического контрапоста (отитал. contrapposto — противоположность), приема изображения, при котором положение одной части тела контрастно противопоставлено положению другой части. Иногда эту статую также называли «Канон Поликлета», даже предполагали, что Поликлет исполнил статую для того, чтобы другие пользовались ею как образцом.

Логарифмическая спираль - образованная вращающимися квадратами

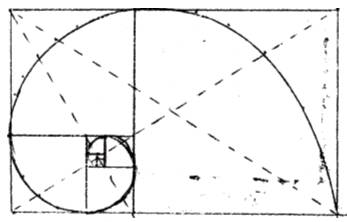Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие прямоугольники. Точки, делящие стороны прямоугольника, в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся внутрь. Полюс лежит на пересечении пунктирных диагоналей. Мы получили закручивающуюся спираль.

Предыдущая спираль была правой, данная является левой. Идет процесс противоположный предыдущему: с ростом, накоплением информации, энтропия убывает.

Мы рассматриваем модель в проекции на плоскость. Рассмотрим ее в пространстве. Известно, что при стереографической проекции полушария в логарифмическую спираль,проектируетсялоксодрома. Т.е., это линия на сфере, которая пересекает все меридианы под одним и тем же углом, как и логарифмическая спираль, которая пересекает под одним и тем же углом радиус-векторы.

Свойства логарифмической спирали универсальны и обладают рядом замечательных свойств. Их широко используют, например, в технике. Лезвия вращающихся ножей в резальных машинах, имеют форму логарифмической спирали, благодаря чему угол резания остается постоянным. В гидротехнике: по логарифмический спирали закручивают трубу, подводящую воду к лопастям. Логарифмическую спираль, применяют при проектировании специальных зубчатых передач. На земном шаре, локсодрома определяет самый удобный куре судна в открытом океане: угол между его курсом и магнитной стрелкой, остается неизменным. Как уже говорилось, по логарифмической спирали, свернуты многие ракушки, семена подсолнечника в корзинке и т. д.

Много внимания, изучению логарифмической спирали, уделили такие математики, как Р. Декарт, Торричелли, Бернулли. Последний, открыв свойство спирали, оставаться неизменной при различных геометрических преобразованиях плоскости, былнастолько поражен этим свойством, что завещал, после его смерти, написать на могиле: "Измененная, не изменяюсь" Название этой замечательной кривой дал П. Вариньон, в начале 18 ст.

Это, действительно, замечательная кривая. Она описывает многие естественные процессы в Природе, явления, отвечающие экстремальным принципам, асимметрии живого, экономии энтропии и т.д. Поэтому, выбор, в качестве модели движения эволюции системы, логарифмической спирали и локсодромы, вполне оправдан. Ее свойства так же универсальны, как у Золотого сечения и ряда Фибоначчи.

Таким образом, моделью эволюции, выбираем сферу с развивающейся локсодромой на ее поверхности. Модель обратного процесса - снижения энтропии, отражает локсодрома завивающаяся в обратном порядке.

Ноосфера привязана к конкретной геосистеме. А как уже говорилась ранее, геосистема моделируется додекаэдром, вписанном в структуру икосаэдра. Полагая, что биосфера развивается по такой же модели, как и геосистема (учитывая их соразмерность), принимаем, пространственную модель эволюции биосферы, аналогичной.

Известно, что додекаэдр двойствен (дуален) икосаэдру - центры граней правильного икосаэдра, являются вершинами правильного додекаэдра. Т.е.,описанная вокруг додекаэдра сфера, является вписанной в икосаэдр. Кроме этой сферы, в состав модели, войдут еще две: вписанная в додекаэдр и описанная вокруг икосаэдра.

Процесс эволюции системы, описывают локсодромы на средней сфере. Каждой точке на локсодроме, соответствует определенное время. Динамика процессов эволюции ритмична и выражается пульсацией средней сферы. Ее радиус изменяется от меньшей (вписанной) сферы,до большей (описанной).

Свойства системы, протекание процессов, зависят от того поля влияния (додекаэдра или икосаэдра), в котором находится сфера моделирования, и зависит от отраженных свойств этих тел.

Учитывая, что локсодромы описываются, различными по конструкции фигурами, они имеют различный коэффициент роста, зависящий, так же, и от других причин. Информационная локсодрома влияет на энтропийную, но это влияние, не прямо. На энтропию влияют и другие подсистемы и факторы.

Данная модель схематична и крайне упрощена. Тем не менее, даже такую, изобразить на плоскости - ненаглядно и сложно для восприятия. Для наглядности проверки достоверности модели и прогнозирования, в первом приближении, необходимо, как минимум, использовать компьютерную графику и анализ. Чем больше других моделей будет наложено на эту, тем реальнее будет модель, и точнее прогнозирование.

24.Древнеегипетский канон пропорционирования. Египетский треугольник и сетка.

КАНОН ДРЕВНЕЕГИПЕТСКИЙ (от греч. kanon — закон, норма), свод правил, присущий художественной культуре Древнего Египта и сложившийся в эпоху Раннего царства (I—II династии). К. д. формировался и закреплялся в ходе многовекового отбора и главным образом в связи с древнеегипетскими культами власти и загробного существования. Если для античного канона обоснование пропорций и др. элементы вытекают из пластически зримой природы окружающего мира, то К. д. отличается подчеркнутой эстетизацией математического, точнее, геометрического начала.

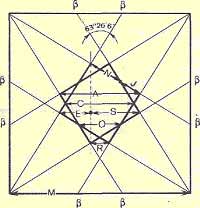Квадрат канонических пропорций искусства Древнего Египта

К. д. отличает строгая систематичность и взаимосвязанность всех основных элементов. Он объединял принципы композиции, иконографию, художественные техники и отдельные приемы изображения вплоть до мелких деталей. Важнейшей особенностью К. д. является гармоничное сопряжение изобразительного ряда и иероглифов элементов иероглифики. Как и в искусстве Восточной Азии, египетская иероглифика сочетала в себе знаково-символическое и собственно эстетическое начала. Начертания некоторых оказали воздействие на композицию и контуры канонических изображений.

Построение канонического типа изображения

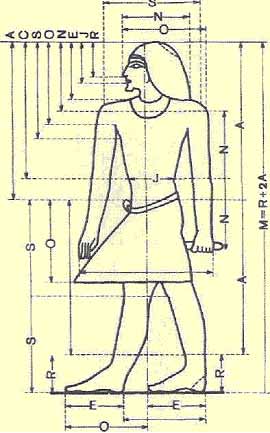Среди разнообразных компонентов К. д. особая роль принадлежит пропорциональным соотношениям, которые составили математическую и одновременно символическую его основу. К. д. опирался на восемь пропорциональных величин, полученных из геометрических построений после деления сторон исходного квадрата в отношении золотого сечения. Пересечение диагоналей, проведенных в точки деления сторон в пропорции золотого сечения (J3), образует два малых квадрата. Искомые восемь пропорциональных величин составляют отрезки между вершинами и точками пересечения сторон малых квадратов. Это (в порядке возрастания) величины R, J, E, N, к, S, С, А. При этом треугольники, образованные диагоналями . большого квадрата, геометрически подобны граням пирамид в Гизе. Для канонических типов статуй и рельефов максимальный размер фигуры соответствует стороне большого квадрата. Местоположение отдельных элементов фигуры —- уровень носа, рта, шеи, плеч, пояса и т. д. — определяется восемью последовательно возрастающими величинами, отмеряемыми от верхнего предела. Благодаря мастерскому применению системы пропорций, в одном и том же изображении могли органично сочетаться элементы человеческой фигуры и тела животного (примером может служить Большой Сфинкс в комплексе фараона Хефрена в Гизе).

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

Египетский треугольник

Особенностью такого треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Египетский треугольник является простейшим (и первым известным) изГероновых треугольников — треугольников с целочисленными сторонами и площадями.

Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.

Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами. В архитектуре средних веков египетский треугольник применялся для построения схемпропорциональности.

Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

25.Дорический ордер, его строение и пропорции. Построение энтазиса.