Вариант 25

Задача 1. Три студента пошли сдавать экзамен. Первый сдаст успешно с веро­ятностью 0,9, второй – 0,5, третий – 0,2. Найти вероятность того, что экзамен сдадут два студента.

Задача 2. Из множества чисел {1, 2, 3, …, 20} наудачу последовательно и без возвращения извлекают два числа. Найти вероятность того, что пер­вое число больше второго не менее чем на 5?

Задача 3. Дана функция распределения F_(х) случайной величины . Найти плотность р_(х), коэффициент с, М, D, , вероятность попадания  в промежуток [a; b).

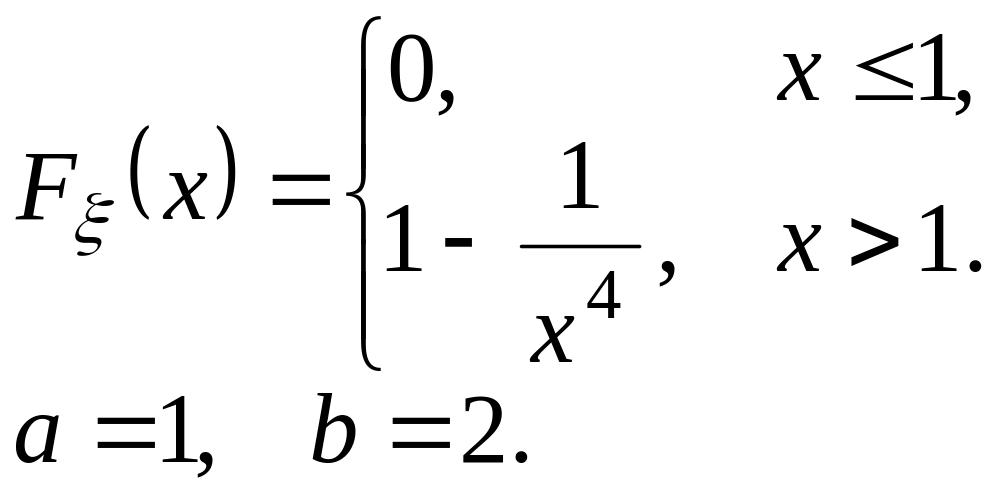
Задача 4. Известны М и D случайной величины , имеющей равномерное распределение на отрезке [a; b]. Найти плотность р_(х), функцию распре­деления F(x), построить ее графики. Найти P{c₁ <  < c₂}.

М = 1, D = 3, с₁ = 0, с₂ = 6.

Задача 5. Для схемы Бернулли (n – число испытаний, р – вероятность успеха в одном испытании) определить вероятность осуществления события {k₁<k<k₂}, где k – количество успехов, пользуясь теоремой Муавра – Лап­ласа: n = 1200, p = 1/4, k₁ = 270, k₂ = 340.

Задача 6. Система случайных величин (; ) имеет совместную плотность f(x;y). Найти с, плотности f_(x), f_(y) и коэффициент корреляции.

Задача 7. По результатам наблюдений случайной величины составлен дис­кретный вариационный ряд (x_i – элементы выборки, n_i – частоты).

1. Найти объем выборки и ее размах.

2.Составить интервальный вариационный ряд.

3. Построить гистограмму и эмпирическую функцию распределе­ния.

4. Найти точечные оценки медианы, математического ожидания и дисперсии (смещенную и несмещенную).

5. Считая, что генеральная совокупность распределена по нормаль­ному закону, найти доверительные интервалы для математиче­ского ожидания и дисперсии с доверительной вероятностью 1 - .

6. С помощью критерия ² проверить при уровне значимости ₁ ги­потезу про нормальное распределение генеральной совокупности.

xi	8,7	8,9	9,3	9,5	9,7	10,1	10,3	10,7	 = 0,1
ni	2	4	3	6	5	6	3	1	1 = 0,01