
- •Введение в математическую экономику
- •1. Предмет и задачи математической экономики
- •2. Математическое моделирование экономических систем
- •3. Примеры экономических задач оптимизации и управления
- •4. Общая схема принятия решений. Виды и параметры экономических задач оптимизации и управления
- •5. Оптимальное поведение и его формализация в экономико-математических моделях
- •Тема 1. Элементы финансовой математики
- •1.1. Сущность финансовой математики
- •1.2. Основные категории, используемые в финансово–экономических расчетах
- •1.3. Фактор времени в финансово–экономических расчетах
- •1.4. Наращение
- •1.5. Дисконтирование
- •1.6. Номинальная и эффективная ставка
- •1.7. Эквивалентность процентных ставок
- •1.8. Сущность инфляции
- •1.9. Учет инфляции при расчете наращивания
- •1.10. Кредитные расчеты. Равные процентные выплаты
- •1.11. Погашение долга равными суммами
- •1.12. Равные срочные выплаты
- •1.13. Потребительский кредит
- •Тема 2. Оценка инвестиционных процессов
- •2.1. Особенности инвестиционных процессов
- •2.2. Чистый приведенный доход
- •2.3. Срок окупаемости
- •2.4. Внутренняя норма доходности
- •2.5. Построение оптимального портфеля
- •2.6. Моделирование финансовых рисков
- •2.7. Принципы определения цены
- •2.8. Простейший и классический процессы риска
- •Тема 3. Основы актуарной математики
- •3.1. Предмет актуарной математики
- •3.2. Использование решающего правила Байеса
- •3.3. Задача о разорении. Вероятность разорения
- •3.4. Сложные пуассоновские процессы
- •3.5. Неравенство Лундберга
- •3.6. Определение вероятности окончательного разорения в экспоненциальном случае
- •3.7. Влияние перестрахования на вероятность разорения. Задача о разорении и перестрахование
- •Тема 4. Задачи оптимизации и управления в экономике
- •4.1. Основные понятия исследования операций
- •4.2. Классификация задач исследования операций
- •4.3. Построение экономико-математической модели
- •4.4. Линейное программирование
- •4.5. Геометрический метод решения задачи линейного программирования
- •4.6. Симплекс-метод решения задачи линейного программирования
- •4.7. Транспортная задача линейного программирования
- •4.8. Задача коммивояжера и метод ветвей и границ
- •2) Построение нижних и верхних оценок минимального значения целевой функции.
- •3) Отсеивание вариантов.
- •4.9. Нелинейное программирование. Метод множителей Лагранжа
- •4.10. Задача выпуклого программирования
- •4.11. Понятие о параметрическом и стохастическом программировании
- •4.12. Общая постановка задачи динамического программирования
- •4.13. Принцип оптимальности и уравнения Беллмана
- •4.14. Задача о распределении средств между предприятиями
- •4.15. Общая схема применения метода дп. Задача об оптимальном распределении ресурсов между отраслями на n лет
- •Тема 5. Математические модели экономических процессов
- •5.1. Линейные модели экономики
- •5.2. Модель Леонтьева «Затраты-выпуск»
- •5.3. Планирование производства в динамике (модель Неймана «расширяющейся» экономики)
- •5.4. Математическая теория потребления. Формализация предпочтения потребителя при выборе товаров
- •5.5. Функция полезности как критерий оценки товаров
- •5.6. Предельный анализ и понятие эластичности в теории потребления
- •5.7. Оптимизационная модель задачи потребительского выбора. Уравнение Слуцкого
- •5.8. Математическая теория конкурентного равновесия
- •5.9. Рыночный спрос и рыночное предложение. Условия совершенной конкуренции. Модель Вальраса
4.15. Общая схема применения метода дп. Задача об оптимальном распределении ресурсов между отраслями на n лет
Прежде чем перейти к конкретным задачам, следует усвоить общую схему применения метода ДП.
Предположим, что все требования, предъявляемые к задаче методом ДП, выполнены. Построение модели ДП и применение метода ДП для решения сводится к следующим моментам:
1. Выбирают способ деления процесса управления на шаги.
2.
Определяют параметры
состояния
![]() и
переменные управления
и
переменные управления
![]() на
каждом шаге.
на
каждом шаге.
3. Записывают уравнения состояний.
4. Вводят целевые функции k-го шага и суммарную целевую функцию.
5.
Вводят
в рассмотрение условные максимумы
(минимумы)
и
условное оптимальное управление на k-м
шаге:
,
![]() .
.
6.
Записывают
основные для вычислительной схемы ДП
уравнения Беллмана
для
и
,
![]() .
.
7. Решают последовательно уравнения Беллмана (условная оптимизация) и получают две последовательности функций:
![]() и
и
![]()
8. После выполнения условной
оптимизации получают оптимальное
решение для конкретного начального
состояния
![]() :
:
![]() и
и
по цепочке
![]() оптимальное
управление:
оптимальное
управление:
![]() .
.
Решая задачи, следует по возможности придерживаться этой схемы по крайней мере в начале изучения темы. Рассмотрим, как работает схема на примере задачи об оптимальном распределении ресурсов между двумя отраслями на n лет.
Планируется деятельность
двух отраслей производства на n
лет. Начальные ресурсы
.
Средства x,
вложенные в I
отрасль в начале года, дают в конце года
прибыль
и
возвращаются в размере
![]() ;
аналогично для II
отрасли функция прибыли равна
,
а возврата —
;
аналогично для II
отрасли функция прибыли равна
,
а возврата —
![]()
![]() .
В конце года все
возвращенные средства заново
перераспределяются между I
и II
отраслями,
новые средства не поступают, прибыль в
производство не вкладывается.
.
В конце года все
возвращенные средства заново
перераспределяются между I
и II
отраслями,
новые средства не поступают, прибыль в
производство не вкладывается.
Требуется распределить имеющиеся средства между двумя отраслями производства на n лет так, чтобы суммарная прибыль от обеих отраслей за n лет оказалась максимальной.
Необходимо:
построить модель ДП для задачи и
вычислительную схему; решить задачу
при условии, что
![]() ед.,
n=4,
ед.,
n=4,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Процесс
распределения средств между двумя
отраслями
производства разворачивается во времени,
решения принимаются
в начале каждого года, следовательно,
осуществляется деление на шаги: номер
шага — номер года. Управляемая система
— две отрасли производства, а управление
состоит в выделении
средств каждой отрасли в очередном
году. Параметры состояния
к началу k-го
года —
(k=l,
2,..., n)
— количество средств,
подлежащих распределению. Переменных
управления на каждом
шаге две:
![]() —
количество средств,
выделенных I
отрасли, и
—
количество средств,
выделенных I
отрасли, и
![]() —
II
отрасли. Но так как все средства
—
II
отрасли. Но так как все средства
![]() распределяются,
то
распределяются,
то
![]() ,
и поэтому управление
на k-м
шаге зависит от одной
переменной
,
и поэтому управление
на k-м
шаге зависит от одной
переменной
![]() ,
т.е.
,
т.е.
![]() .
.
Уравнения состояний
![]() (4.21)
(4.21)
выражают остаток средств, возвращенных в конце k-го года.
Показатель эффективности k-го шага — прибыль, полученная в конце k-го года от обеих отраслей:
![]() (4.22)
(4.22)
Суммарный показатель эффективности — целевая функция задачи — прибыль за n лет:
![]() (4.23)
(4.23)
Пусть
—
условная оптимальная прибыль за n-k+1
лет,
начиная с k-го
года
до n-го
года
включительно, при условии, что
имеющиеся на начало k-го
года средства
в
дальнейшем распределялись
оптимально. Тогда оптимальная прибыль
за n
лет
![]() .
.
Уравнения Беллмана имеют вид:
![]() (4.24)
(4.24)
![]() (4.25)
(4.25)
![]()
Используем конкретные данные.
Уравнение состояний (4.11) примет вид:
![]() ,
или
,
или
![]() (4.26)
(4.26)
Целевая функция k-го шага (4.22)
![]()
Целевая функция задачи
![]() (4.27)
(4.27)
Функциональные уравнения
![]() (4.28)
(4.28)
![]() (4.29)
(4.29)
Проводим условную оптимизацию.
IV
шаг.
Используем уравнение (4.28). Обозначим
через
![]() функцию,
стоящую в скобках,
функцию,
стоящую в скобках,
![]() ;
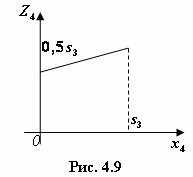
функция
—
линейная, возрастающая, так как угловой
коэффициент 0,1 больше нуля. Поэтому
максимум достигается на конце интервала
;
функция
—
линейная, возрастающая, так как угловой
коэффициент 0,1 больше нуля. Поэтому
максимум достигается на конце интервала
![]() (рис.
4.9).
Следовательно,
(рис.
4.9).
Следовательно,
![]() при
при
III шаг. Уравнение:
![]()
Найдем
![]() из
уравнений состояний (4.26):
из
уравнений состояний (4.26):
![]() и,
подставив
его выражение в правую часть уравнения,
получим
и,
подставив
его выражение в правую часть уравнения,
получим
![]()
![]()
Как и в
предыдущем случае, максимум достигается
при
![]() ;
т.е.
;
т.е.
![]() при
при
![]() .
.
II
шаг. Из уравнения состояния:
![]() .
Поэтому уравнение (4.28) при k=2
примет вид:
.
Поэтому уравнение (4.28) при k=2
примет вид:
![]() .
.
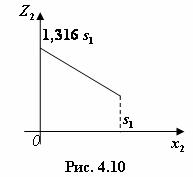
Линейная
относительно
функция
![]() убывает
на отрезке
убывает
на отрезке
![]() и
поэтому ее максимум достигается при
и
поэтому ее максимум достигается при
![]() (рис.
4.10):
(рис.
4.10):
![]() при
при
![]() .
.
I
шаг.
![]() .
Уравнение (4.28) при k=1
имеет вид:
.
Уравнение (4.28) при k=1
имеет вид:
![]()
Как и в предыдущем случае, максимум достигается в начале отрезка, т.е.
![]() при
при
![]() .
.
На этом
условная оптимизация заканчивается.
Используя ее результат
и исходные данные,
получим
![]() ,
,
![]() .
.
![]() ,
,
![]()
(все средства выделяются
II
отрасли)
![]()
![]()
(все средства выделяются II отрасли)
![]()
(все средства выделяются I отрасли)
![]()
(все средства выделяются I отрасли).
Оптимальная прибыль за 4 года, полученная от двух отраслей производства при начальных средствах 10000 ед., равна 15528 ед. при условии, что I отрасль получает по годам (0; 0; 6400; 4480), а II отрасль – соответственно (10000; 8000; 0; 0).
