2. Задача з механіки.

Обчислити роботу, яку викон. змінна сила F при переміщ. матеріальної точки з полож. А у полож. В, яка діє у напрямку переміщення.

Для розв’язання цієї задачі поступ. так:

1.

• ділимо шлях [а, в] точками S_i (i=1, … , n-1) довільно на n частин;

• Тоді S_i - S_{i -1} = S_і ;

2.

• Вибир. є [S_{i -1}, S_i].

• Будемо вважати, що на кожному із відрізків S_і це сила стала і дорівнює з-ню її в т. . F ( ).

3. А_і = F ( ) S_і

А_n = F ( ) S_і

А А_n

Природно, що за роботу, яку викон. це сила F на в-ку [а, в] слід прийняти:

;

Обидві зад. привели нас до обчисл. однотипних границь.

2. Нехай задана функція у=f(х), х є [а, в].

1. Ділимо в-зок [а, в] дов. способом на т. х_і на n частин.

Довжину кожного із в-ків х_і – х_і-1 = х_і.

Ці в-ки назив. частинними.

2. На кожному з цих частин. в-ків вибир. довільно і обчисл. з-ня в кожній з цих точок.

3. Склад. суму добутків:

= .

Це сума назив. інтегр. сумою на в-ку [а, в].

4. В-ня: Границя інтегральної суми при умові, що , якщо вона існує і не залежить ні від способу розвит. в-ка [а, в] на част. в-ки, ні від вибору точок на кожному з них назив. визначеним інтегралом від ф-ції f(х) на в-ку [а, в] і познач.: , де а, в – межі інтегрування; а – нижня; в – верхня; f(х) – підінтегр функції; f(х)dx – підінтегр. вираз.

Отже, за визнач. маємо .

Познач: , тоді .

.

Геометричний зміст. Див. зад. 1 (площина кр. трап.).

де , .

Механічний зміст. .

Див. зад. 2.

Суми Дарбу. Надалі будемо вважати не обхід. умова викон.

Очевидно, що якщо f (x) неперервна, то за І т. Веєри вона обмежена і на цьому в-ку прим. своє найб. і найм. значення. , тобто [х_і-1, х_і]. лежить між т_і і М_і. , . Назив нижньою (S) і верхньою (S) інтегральними сумами для фун-ції f (x) , або сумами Дербу. Якщо А помнож. на х_і і просумув., то матимемо , то очевидно, що . Будь-яка інтегр. сума лежить між інтегр. сумами Дербу. Тоді S, S – точні межі для інт. суми б.

Умови існування інтеграла. Для того, щоб інтеграл існував необхідно і достатньо, щоб .

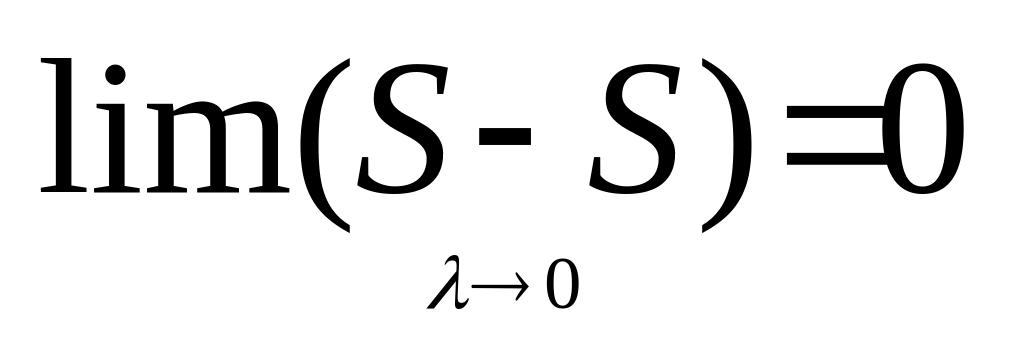Доведення:

1. Необхідність.

Припустимо, що інтеграл існує, тобто , . , але суми S і S при заданому розбитті є для інтегральних сум б відповідно точними верхньою і нижньою границями. Тому для них матиме місце нерівність. Із , .

2. Доступність:

Дано: Нехай , тоді з цієї умови і умови , тоді , але тоді , .

Умови існування визн. інтегр. можна сформулюв. і через колив. фун-ції, яке має практичне тзастосування.

.

Тоді, .

Властивості визначеного інтеграла.

1. ,

,

2. , I<I₁ , I=-I₁ , 2I₁ = 0, I₁=0;

3. ; де С – константа;

4. ;

5. ;

6. а). , ;

б). , ;

7. ;

8. Якщо f(x) інтегр. на [а,b] і обмеж. на ньому , тоді .

Обмеження визначення інтегралів.

1. Якщо Ф(x) є перв. для f(x) на в-ку [а,b], то вона не є єдиною.

Нехай F(x) – ін. перв. для f(x). Тоді, за власт. перв. Ф(х)= F(x)+С; Ф’(х)= f(x), F’(x)= f(x). При х=а , матимемо Ф(а)= F(а)+С=0, а Ф(а)=0. С= - F(а)+Ф(а). С= - F(а). При х= b. , де F(x) – будь-яка первісна. або . Формула Ньютона-Лейбніца Основна формула інтегр. числення.