
- •1. Аналіз поняття множини. Потужність множини. Зчисленні множини та їх властивості. Множини натуральних чисел n, цілих z, раціональних q, та дійсних чисел r, їх потужність.
- •2. Множина дійсних чисел r, її властивості. Поняття верхньої і нижньої граней числової множин, їх існування і властивості. Теорема Кантора.
- •3. Границя послідовності. Основні теореми про збіжність послідовностей. Границя обмеженої монотонної послідовності. Число е. Границя послідовності в метричному просторі.
- •4. Поняття функції. Способи задання функцій. Функції n дійсних змінних та комплексної змінної. Поняття функції в школі.
- •Словесний.
- •6. Неперервність функції в точці і на відрізку. Неперервність функції кількох змінних та функцій комплексної змінної. Поняття рівномірної неперервності.
- •7. Основні теореми про неперервність функції
- •8. Розвиток поняття степеня. Степенева ф-я в дійсній та комплексній області /означення, властивості/. Степенева ф-я в школі.
- •9. Показникові ф-я дійсній та комплексній змінної (означення, властивості). Показникові ф-я в школі.
- •10. Логарифмічна ф-ія дійсної та комплексної змінної (означення, властивості). Розклад її в степеневий ряд. Логарифмічна ф-ія в школі.
- •13. Похідна ф-ії комплексної змінної. Умови диференційовності. Аналітичні ф-ії.
- •14. Теорема Ролля. Т-ма Лагранжа. Т-ма Коші.
- •15.Екстремуми ф-ції. Опуклість і точки перегину. Асимптоти.
- •16. Первісна та її властивості, невизначений інтеграл. Основні методи інтегрування.
- •17. Визначений інтеграл та умови його існування. Формула Ньютона-Лейбніца, вивчення інтеграла в школі.
- •1. Задача про обчислення площі кривої трапеції.
- •2. Задача з механіки.
- •19. Поняття метричного простору. Повні метричні простори.
- •20. Теорема Банаха про стискуючі відображення та її застосування.
- •21. Числові ряди з дійсними та комплексними членами, основні поняття. Необхідна умова збіжності. Геометрична прогресія та гармонічний ряд. Властивості збіжних рядів.
- •22.Ознаки збіжності рядів з додатними членами. Ряди з довільними членами, їх абсолютна та умовна збіжність, властивості.
- •23. Степеневі ряди з дійсними та комплексними членами. Абсолютна збіжність. Інтервал та радіус збіжності.
- •25.Застосування інтегрального числення до розв-ня задач геометрії і фізики.
- •1. Площа фігури.
- •26. Обернені тригонометричні функції дійсної та комплексної змінної (означення, властивості).
- •27. Означення поняття теорії диференц. Рівнянь: порядок, розв’язок, загальний розв’язок, інтегральна крива, початкові умови, задача Коші.
- •28. Диф. Рівняння з відокремлюваними змінними, лінійні рівняння та рівняння, що зводяться до них.
- •30. Лінійні диф. Рівняння вищих порядків із сталими коефіцієнтами та їх застосування до вивчення коливних процесів.
4. Поняття функції. Способи задання функцій. Функції n дійсних змінних та комплексної змінної. Поняття функції в школі.
Нехай
нам дано дві множини
![]() ,
У={у}. Відображенням множини Х на (в) множ.
,
У={у}. Відображенням множини Х на (в) множ.
![]() (на
(в)) називається закон (правило) по якому
кожному елементу множини Х ставиться
у відповідність єдиний елемент у є У,
друг.
(на
(в)) називається закон (правило) по якому
кожному елементу множини Х ставиться
у відповідність єдиний елемент у є У,
друг.
Закон
позн. буквою f.
![]()
Якщо Х – числова множ., то таке відображення називається функцією.
Визначення функції :
Якщо кожному числу х за певним правилом поставлено у відповідність одне дійсне число у, то кажуть, що на множині х задана функція і позначають у = f(х).
Множина
х при цьому називається областю визначення
функції у
= f(х). Множина
елемент чисел
![]() назив. множ. значень функції.
назив. множ. значень функції.
Отже, для того, щоб функція була заданою треба знати область визначення функції, закон відповідності по якому кожному елементу х відповідає у.
у=![]() ,
х
,
х![]() ;
у=
;
у=![]() ,
х
,
х![]() ;
у=
;
у=![]() .
.![]() ,
х є R; у=
.
,
х>0.(існування).
,
х є R; у=
.
,
х>0.(існування).
Способи задання функції
Аналітичний (це стос.. коли функція задається аналітичним виразом).
Табличний (за допомогою таблиць)
Графічний (зад. графіками). Графіком функції
 наз. множина точок площини з координатами
наз. множина точок площини з координатами

Словесний.
Класифікація функції
Основні
елементарні функції:
1)
![]() ;
2)
;
2)
![]() (степенева
фу–я);
3)
(степенева
фу–я);
3)
![]() (показникові);
4)
(показникові);
4)
![]() (логарифмічна
функція)
(логарифмічна
функція)
5)
![]() (тригонометрична)
6)
(тригонометрична)
6)
![]() 7)
7)
![]()
Поняття функції в школі:
1. Функцією наз. залежність змінної у від змінної х, при якій кожному значенню змінної х відповідає єдине значення змінної у. Функцію позначають або однією буквою латинського алфавіту f, F або за допом. рівності , змінну х назив. незалежною змінною або аргументом .Змінну у залежною змінною або функцією. Всі значення незалежної змінної утворюють область визначення фу-ї. Усі значення, які набуває залежна змінна, утворюють область значень функції.
2.Числова
функція. В
алгебрі і початках аналізу окремо
позначається числова
фу –я:
числовою
фу-ю назив. залежність між елементами
двох множин дійсних чисел Х
і У,
при якій кожному числу х з множини Х
відповідає
деяке цілком визначене число у з множини
У.
Цю
залежність записують
![]() ,
де х – аргумент; у – функція. При цьому
множина Х
наз.
областю визначення фу-ї і
записується
,
де х – аргумент; у – функція. При цьому
множина Х
наз.
областю визначення фу-ї і
записується
![]() , а множина У
– областю
значень фу-ї, і
запис.
, а множина У
– областю
значень фу-ї, і
запис.
![]() .
.
3.
Складена
фу-я.
Фу-ю виду
![]() або
або
![]() ,
де
,
де
![]() наз.
складеною
фу-ю. Змінну
у наз. проміжним
аргументом.
наз.
складеною
фу-ю. Змінну
у наз. проміжним
аргументом.
Функція
дійсної змінної: Нехай
для довільного
![]() визначені
фу-ї
визначені
фу-ї
![]() ,
розглянемо фу-ю
,
розглянемо фу-ю
![]() (1).
Ця фу-я є комплексно значною від дійсної
змінної.
(1).
Ця фу-я є комплексно значною від дійсної
змінної.
![]()
Фу-я (1)
в точці
![]() має
границю, якщо в цій точці існують границі.
має
границю, якщо в цій точці існують границі.
![]()
Функція
комплексної змінної:
нехай кожному елементу z з деякої множини
Е за певним законом поставимо у однозначну
відповідність компл. число із множн.
![]() ,
тоді на мн.
,
тоді на мн.
![]() комплексно
значна фу-я комплексної змінної. Їх
називають комплексними
фу-и змінної.
комплексно
значна фу-я комплексної змінної. Їх
називають комплексними
фу-и змінної.
![]() ,
,
![]()
5. Границя функції в точці. Властивості границь. Визначні границі. Границі функції в метричних просторах та функцій комплексної змінної.
![]() ,
,
![]() гранична
точка множини Х.
гранична
точка множини Х.
Означення:
Точка назив. граничною точкою множини Х, якщо у будь-якому околі цієї точки міститься принаймні одна точка цієї множини. Інакше грани. точка назив. точкою скупчення.
Гранична точка може належати множині і неналежати.
Визначення 1 (за Коші):
Число А
назив. границею
функції
при
![]() і якщо для будь-якого
і якщо для будь-якого
![]() існує
таке
,
що з нерівності
існує
таке
,
що з нерівності
![]() нерівність
нерівність
![]() .
.
Визначення 2 (за Гейне)
Число А
назив. границею
функції
при
![]() і,
яку б послідовність значень не пробігала
змінна
і,
яку б послідовність значень не пробігала
змінна
![]() збіжна
до
відповідна
послідовність значень функції буде
збіжною до числа А.
збіжна
до
відповідна
послідовність значень функції буде
збіжною до числа А.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
Властивості границь.
Якщо фу-я
 має
границю в точці
має
границю в точці
 ,
то ця границя єдина.
,
то ця границя єдина.Якщо
 для
всіх х з деяким околом точки
,
крім, можливо самої точки
має
границю, то
для
всіх х з деяким околом точки
,
крім, можливо самої точки
має
границю, то
 .
. для
всіх х
у
деякому околі точки
,
крім, можливо самої точки
,
і фу-ї
й а(х)
у
точці
мають
ту саму границю b,
то і фу-я
для
всіх х
у
деякому околі точки
,
крім, можливо самої точки
,
і фу-ї
й а(х)
у
точці
мають
ту саму границю b,
то і фу-я
 в
точці
має
границю, що дор. цьому самому числу b
в
точці
має
границю, що дор. цьому самому числу b
Нехай
фу-ї
і
![]() визначені
в деякому околі точки
,
крім можливо самої точки
,
і нехай існують
визначені
в деякому околі точки
,
крім можливо самої точки
,
і нехай існують
![]() і
і
![]() .
Тоді:
.
Тоді:


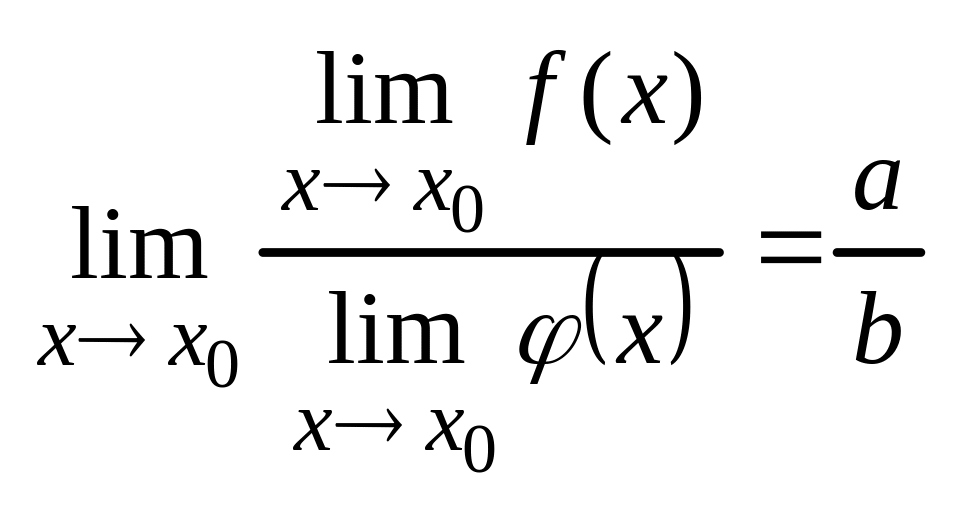 ,
якщо
,
якщо



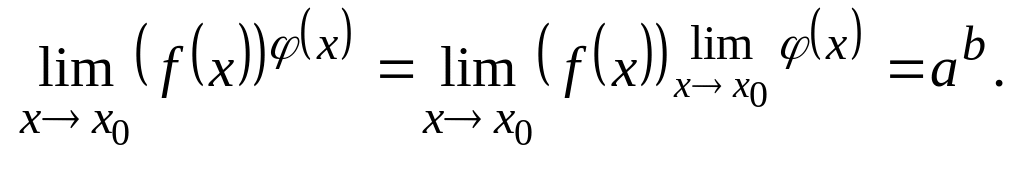
Визначні
границі:![]() Доведення:
Доведення:
![]() .
.
![]() .
Поділимо обидві частини на
.
Поділимо обидві частини на
![]() Для
досить малих
Для
досить малих
![]() будь-яка
крива за
пряму
будь-яка
крива за
пряму
![]() ,
це і доводить, що
,
це і доводить, що
![]()

 В
В
О х
![]() -
друга визначна границя. Доведення:
-
друга визначна границя. Доведення:
![]() нехай
пробігає деяку послідовність
нехай
пробігає деяку послідовність
![]() -
ціла частина.
-
ціла частина.
![]() при
при
![]() ,то
,то
![]() додаємо
1і підносимо до степеня:
додаємо
1і підносимо до степеня:
 -
границя лівої.
-
границя лівої.
![]() -
границя правої.
-
границя правої.
![]() Нехай
Нехай
 Таким
чином можемо записати, що
Таким
чином можемо записати, що
![]()
