22.Ознаки збіжності рядів з додатними членами. Ряди з довільними членами, їх абсолютна та умовна збіжність, властивості.

Якщо всі члени ряду невід’ємні, то він назив. рядом з додатними членами – ця послідовність зростаюча, бо члени ряду достатні.

Для того, щоб ряд з додатними членами був збіжним, необхідно і достатньо, щоб послідовність часткових сум була зростаючою і обмеженою зверху.

Властивості (ознаки збіжності):

1. Якщо більший ряд збіжний, то і менший, якщо менший ряд розбіжний , то і більший розбіжний.

2. Гранична ознака:

Якщо границя відношення загальних членів двох рядів = с = const (с≠0), то обидва ряди одночасно збіжні або розбіжні.

3. Достатня ознака Даламбера:

Якщо в додатному ряді

де r – деяке число, тоді

4. Радикальна ознака збіжності Коші: якщо , то

Інтегральна ознака Коші: Якщо ф-я f(x) визначена на проміжку і при , неперервна, додатна, спадна, то для того, щоб збігався числовий необхідно і достатньо, щоб збігався невласний інтеграл:

Ряд , в якому числа можуть бути як додатними, так і від’ємними, назив. знакозмінним рядом.

Ряд – назив. знакопочередним.

Нехай дано знакопочередний ряд(1). Він назив. абсолютно збіжним, якщо збіжним є ряд, утворений з модулів членів даного ряду.

(1)

(2)

Ряд (1) назив. умовно збіжним, якщо цей ряд є збіжним, а ряд (2) – розбіжний.

Щоб дослідити ряд на умовну чи абсолютну збіжність слід:

1. скласти ряд з абсолютних величин членів ряду і дослідити на збіжність як для додатних рядів.

а) Якщо ряд (2) збіжний, то (1) абсолютно збіжний.

б) Якщо ряд (2) – розбіжний, то

2) досліджуємо ряд (1) за ознакою Лейбніца.

Ознака Лейбніца: Якщо в знакозмінному ряді члени ряду монотонно не зростають і то такий ряд збіжний.

Властивості:

Не всі властивості(закони арифметики) скінченних сум переносяться на абсолютно і умовно збіжні ряди. Для абсолютно збіжних рядів мають місце сполучний та переставний закони.

Для умовно збіжних рядів має місце сполучний закон і не має переставний.

23. Степеневі ряди з дійсними та комплексними членами. Абсолютна збіжність. Інтервал та радіус збіжності.

Ряд виду де – коефіцієнт ряду, – фіксоване число, – назив. степеневим.

Якщо цей ряд збіжний до своєї суми S(x), то кажуть, що ф-я S(x) розкладається у степеневий ряд в околі т. :

(*)

Теорема Абеля: якщо степеневий ряд (*) збігається в точці в точці , то він збігається і при тому абсолютно при всіх x, що задовольняють умові

Нехай маємо степеневий ряд: і існують точки, відмінні від нуля, у яких ряд збіжний, і точки, в яких він розбіжний. Тоді R, таке, що при всіх х:

– ряд збігається, а при а х: – розбіжний.

Інтервал (-R,R) назив. інтервалом збіжності степеневого ряду, а R – радіусом збіжності.

Якщо ряд збіжний лише в одній точці, то R=0. Якщо ж ряд збіжний на всій числ. осі, то R=∞.

В область збіжності входить інтервал (-R,R) і можливо й кінці.

Аналогічно для степеневого ряду комплексної змінної z:

де коефіцієнтами ряду можуть бути будь-які комплексні числа, справедлива теорема Абеля, аналогічні означення інтервала та радіуса збіжності.

Властивості степеневих рядів в інтервалі збіжності.

Будемо розрізняти терміни: всередині інтервалу збіжності і в інтервалі збіжності. Всередині – на кожному сегменті, що входить в інтервал збіжності. А в інтервалі – для кожного х з інтервалу.

1. Степеневий ряд виду збігається рівномірно всередині інтервалу збіжності.

2. Сума степеневого ряду є ф-я неперервна в інтервалі (-R,R).

3. Степеневий ряд виду можна почленно інтегрувати всередині інтервалу збіжності, зокрема на сегменті :

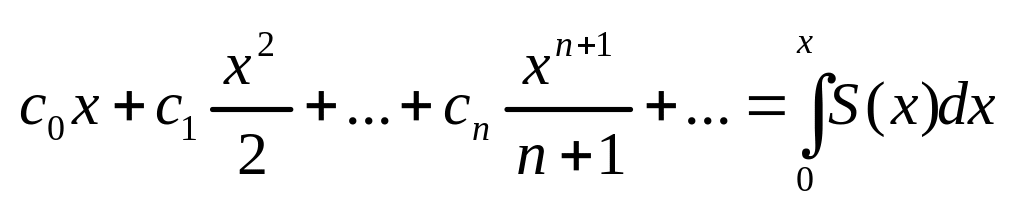
4. Степеневий ряд можна почленно диференціювати в інтервалі збіжності (-R,R): .

Теорема: радіус збіжності проінтегрованих та продиференційованих рядів такий самий, як радіус збіжності вихідного ряду.

24.Ф-ла Тейлора та ряд Тейлора. Біноміальний ряд.

Нехай маємо ф-ю f(x), яка в околі точки має похідні всіх порядків. Утворимо числа:

і складемо ряд виду , який носить назву ряду Тейлора. Ф-ла Тейлора для ф-ї f(x) має вигляд , тому кажуть, що ряд Тейлора породжений ф-єю f(x).

Теорема: Нехай ф-я f(x) в околі точки має похідні всіх порядків. Для того щоб ряд Тейлора збігався до f(x) необх. і достатньо, щоб залишковий член ф-ли Тейлора , коли .

Таким чином, якщо ф-цію f(x) можна розкласти в степеневий ряд по степенях різниці , то цей ряд обов’язково є рядом Тейлора для цієї ф-ї.

Розклад в ряд Тейлора основних елементарних ф-й.

Розклад у ряд Т. в околі т. назив. ще рядом Маклорена.

Спосіб розкладу ф-цій у ряд Тейлора:

1) знаходимо похідні всіх порядків ф-цій f(x);

2) обчислюємо їх значення в точці .

3) складемо формально ряд Тейлора:

4) дослідимо при яких залишковий член ф-ли Тейлора , коли і для таких ставимо «=».

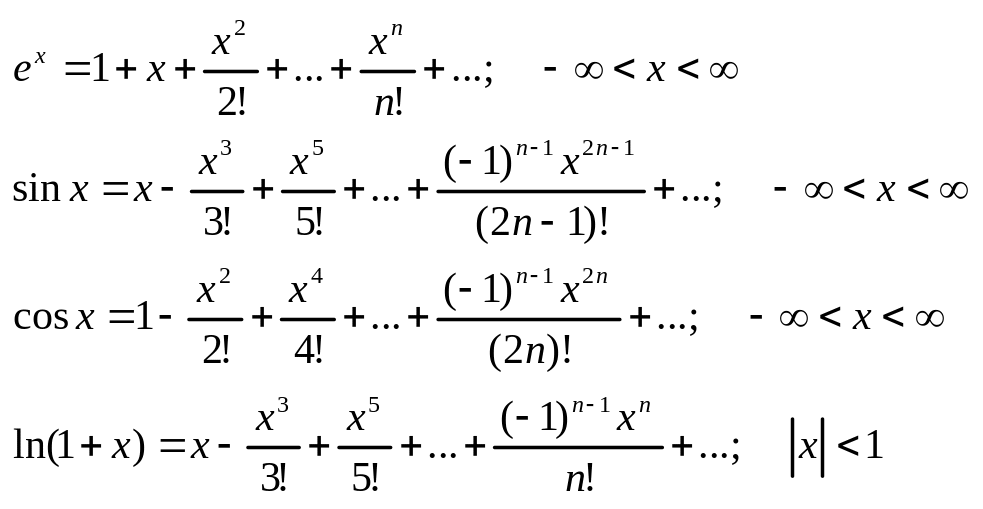
Біноміальний ряд.

Розкладемо в ряд Маклорена ф-цію:

, де – будь-яке дійсне число

Тому

Отже, ряд запишемо у вигляді:

Знайдемо область збіжності ряду. Для цього обчислимо границю відношення наступного члена ряду до попереднього.

Згідно ознаки Даламбера ряд збігається, якщо

Таким чином, біноміальний ряд представляє ф-ю в інтервалі (-1;1)

(-1;1)