17. Ізоморфізм та гомоморфізм груп. Його властивості.

Розглянемо дві групи з бінарною операцією : та з бінарною операцією : . Група наз. ізоморфною групі , якщо існує хоч одне відображення таке, що (1).

Співвідношення (1) для мультиплікативних груп: образ добутку дорівнює добутку образів; для адитивних груп: образ суми дорівнює сумі образів.

Пр. - множина дійсних додатних чисел відносно операції множення: - мультиплікативна абелева група нескінченного порядку, - множина дійсних чисел відносно операції додавання: - адитивна абелева група нескінченного порядку.

В становимо відповідність: .

. Вимога (1) виконується. Групи ізоморфні.

Ізоморфізм потрібний для того, щоб вивчати теорію одних структур за рахунок вивчення певної теорії в другій структурі, бо всі твердження, які мають місце відносно бінарної операції мають місце і відносно бінарної операції в іншій множині. Особливо це притаманне фізиці, механіці.

Основними властивостями ізоморфізму є:

1. При ізоморфізмі образ оберненого елемента дорівнює оберненому елементу образу: .

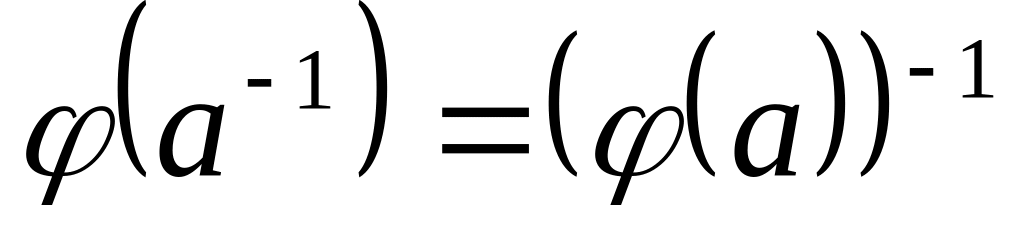2. При ізоморфізмі образ нейтрального елемента переходить в нейтральний елемент.

Довед. , , , .

Дві групи наз. гомоморфними, якщо існує хоча б одним способом міх їх елементами можна встановити відповідність, і не обов’язково взаємо однозначну, але таку, що (1). Очевидно, що всякий ізоморфізм є гомоморфізмом, але не всякий гомоморфізм є ізоморфізмом.

Пр. - група підстановок 3-го степеня відносно множення, - мультиплікативна група чисел .

Якщо парній підстановці співставляємо 1, а непарній співставляємо -1. Тоді буде гомоморфізмом.

Для гомоморфізму є ті ж самі властивості, що і для ізоморфізму.

18. Кільце, приклади кілець. Основні властивості кілець. Ізоморфізм та гомоморфізм груп

Непорожня множина елементів довільної природи, в якій введено дві бінарні операції і і виконується виконання вимог:

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) наз. кільцем.

Зауважимо, що в кільці операція множення не обов’язково комутативна, якщо коммутативна, то кільце наз. комутативним.

Вимоги 6), 7) еквівалентні вимозі, що .

Приклади кілець:

1. натуральні числа відносно додавання та множення не є кільцем, бо не виконуються вимоги 6) та 7).

2. множина цілих чисел відносно додавання та множення очевидно утворює групу.

3. кільцями є множина раціональних, дійсних, комплексних чисел відносно додавання та множення.

4. множина матриць розмірності з раціональними, дійсними, комплексними числами є кільцем.

Властивості кілець:

1. кільце є абелевою, адитивною групою відносно додавання, а тому всі властивості абелевих груп справедливі і для кілець. Крім того,

2. .

Довед.: Покажемо, що є розв’язком даного рівняння: , . Єдність випливає із бінарності операції.

В деяких кільцях нульовий елемент може мати дільники нуля, тобто існують ненульові елементи , , добуток яких є нульовим елементом.

Наприклад, множина матриць розмірності :

.

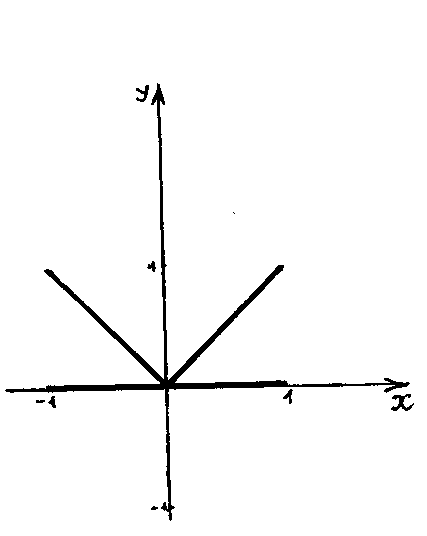
Таким чином, розв’язуючи рівняння над кільцями потрібно пам’ятати про існування кілець з дільниками нуля.

Пр. Кільце неперервних функцій відносно поточкового додавання та множення функцій на сегменті .

, ,

Елемент наз. правим одиничним елементом кільця, якщо .

Елемент наз. лівим одиничним елементом кільця, якщо .

Пр. Розгл. Множину матриць .

, немає єдиного розв’язку. Лівого одиничного елемента не існує.

, , , - є правим одиничним елементом.

Кільце має безліч правих одиничних елементів і ні одного лівого одиничного елемента. Аналогічно можна показати, що множина матриць має безліч лівих і жодного правого одиничного елемента.

Властивості:

1. Є кільця, в яких існують безліч правих одиничних елементів і ні одного лівого одиничного елемента.

2. Є кільця, які мають тільки ліві елементи і ні одного правого.

3. Якщо в кільці є і ліві, і праві елементи, то вони співпадають.

Довед. Методом від супротивного, використовуючи модифікацію: .

Маємо два нейтральних елементи: .

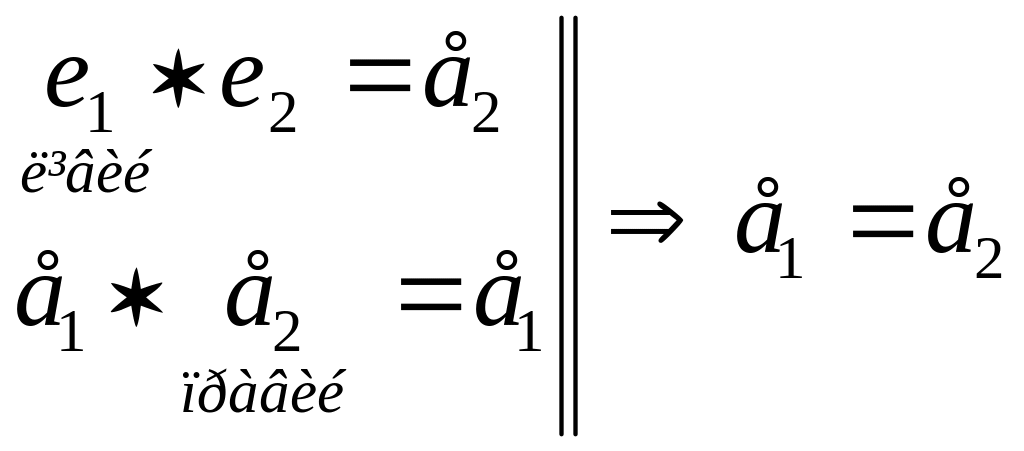2-а кільця наз. ізоморфними, якщо існує хоча б одним способом між їх елементами можна встановити взаємооднозначну відповідність, таку, що якщо існує хоч одне відображення таке, що , .

Два кільця наз. гомоморфними, якщо існує хоча б одним способом між їх елементами можна встановити відповідність, і не обов’язково взаємо однозначну, але таку, що , .

Так як кільце є адитивною групою, то для ізоморфізму та гомоморфізму матимуть місце такі властивості відносно операції додавання.

Ізоморфізм потрібний для того, щоб вивчати теорію одних структур за рахунок вивчення певної теорії в другій структурі, бо всі твердження, які мають місце відносно бінарної операції мають місце і відносно бінарної операції в іншій множині. Особливо це притаманне фізиці, механіці.

Основними властивостями ізоморфізму (гомоморфізму) є:

1. При ізоморфізмі (гомоморфізмі) образ протилежного елемента дорівнює протилежному елементу образу: .

2. При ізоморфізмі (гомоморфізмі) образ нульового елемента кільця переходить в нульовий елемент кільця .
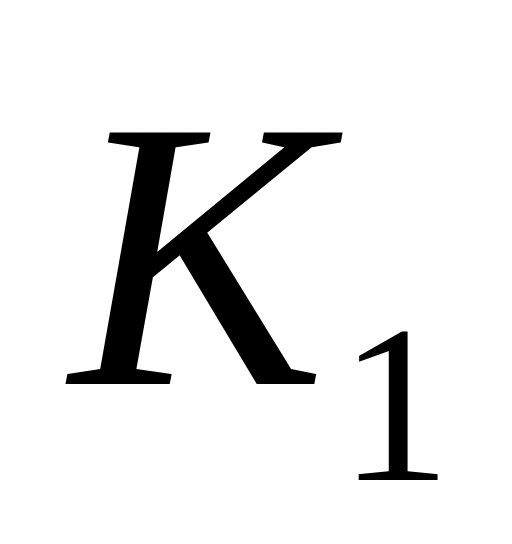