15. Бінарні відношення порядку, його властивості. Мінімальні та максимальні елементи. Впорядковані множини.

Бінарне відношення на множині А наз. відношенням порядку на множині А, якщо воно транзитивне і антисиметричне. Відношення порядку на множині А наз. нестрогим порядком, якщо воно рефлексивне. Відношення порядку наз. строгим порядком, якщо воно антирефлексивне. Відношення порядку наз. лінійним порядком, якщо воно зв'язне. Відношення порядку, яке не є лінійним порядком, ще наз. частковим порядком.

Відношення > і < на числових множинах є відношеннями строгого лінійного порядку. Відношення і на числових множинах є відношеннями нестрогого лінійного порядку. Відношення подільності на множині натуральних чисел є відношенням нестрогого часткового порядку. Відношення включення є відношенням нестрогого часткового порядку на множині всіх підмножин деякої фіксованої множини. Відношення порядку на множині слів, яке застосовується в словниках і полягяє в алфавітному розміщенні слів, називається лексикографічним. Лексикографічний порядок є лінійним порядком.

Якщо на множині А задано відношення часткового (лінійного) порядку , то множина А наз. частково (лінійно) упорядкованою множиною і позначається < А; >. Елемент а А наз. найменшим елементом в А, якщо ). Елемент а А наз. найбільшим елементом в А, якщо .В упорядкованій множині може взагалі не бути найменшого або найбільшого елемента, але якщо він є, то лише один. Справді, якщо в множині А є два найменших елементи а₁ і а₂, то, згідно з означенням найменшого елемента, а₁ а₂ і а₂ а₂, а це можливо лише у випадку а₁= а₂, оскільки відношення антисиметричне. Елемент а А наз. мінімальним елементом множини А, якщо . Елемент а є А наз. максимальним елементом множини А, якщо . Найменший елемент множини А (якщо він існує) є мінімальним елементом в А. Справді, нехай а - найменший елемент в А і нехай для деякого елемента х є А х а . Якщо , то а , оскільки а є найменшим елементом в А. Згідно із властивістю антисиметричності, звідси випливає, що х = а . Отже, х а => х = а , тобто а є мінімальним елементом в А. Аналогічно можна довести, що найбільший елемент множини А є максимальним в А.

В лінійно упорядкованій множині поняття найменшого (найбільшого) і мінімального (максимального) елементів збігаються.

16. Групи. Приклади груп. Основні властивості груп.

Непорожня множина елементів довільної природи, в якій введено одна бінарна операція і виконуються три вимоги:

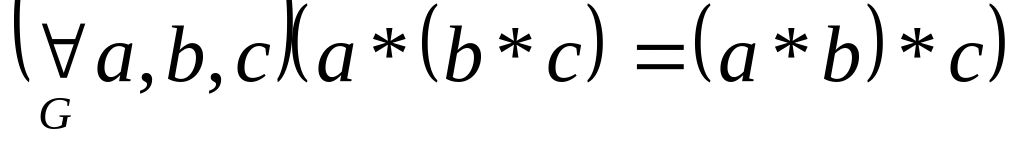• – операція асоціативна,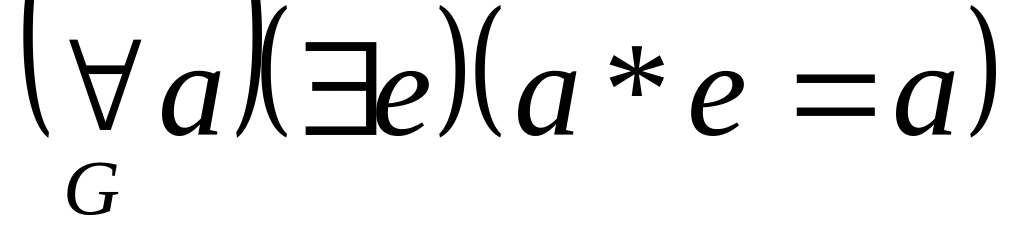

• – існує правий нейтральний елемент,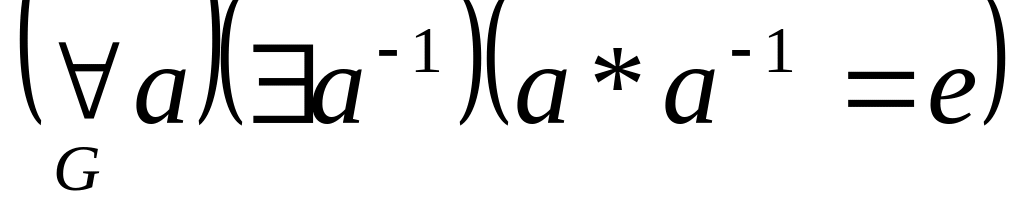

• – кожен елемент має правий обернений, наз. групою.

Зауважимо, що операція в групі в загальному випадку не є комутативною, але якщо операція комутативна, то група наз. комутативною або абелевою. За допомогою груп Абель встановив той факт, що в загальному випадку рівняння степінь яких 5 і більше не можна розв’язати в радикалах.

Якщо операція наз. додавання, то група – адитивна, нейтральний елемент наз. нульовим елементом, наз. протилежним.

Якщо операція наз. множення, то група – мультиплікативна, нейтральний елемент наз. одиничним елементом, називають оберненим.

Кількість елементів скінченої групи наз. порядком групи. Для нескінченних груп порядок замінюється кардинальними числами (наприклад, зчисленність).

Приклади груп.

1. Множина : .

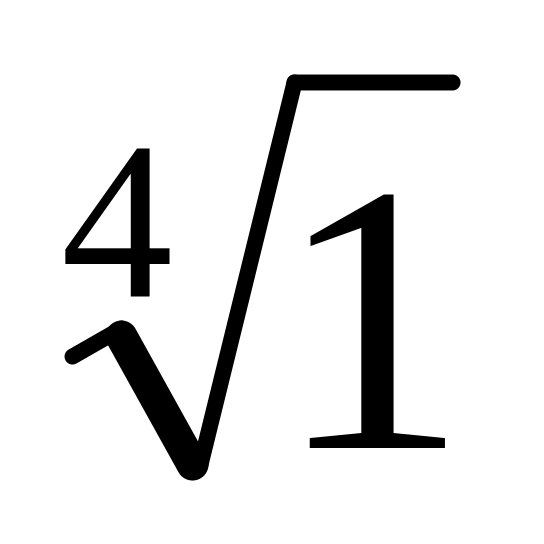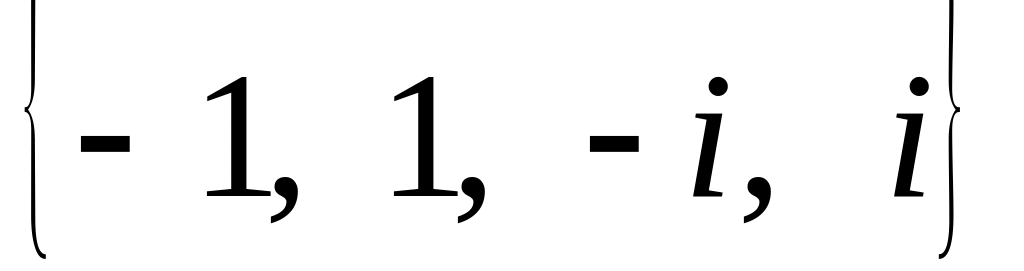	1	-1	і	-і
1	1	-1	і	-і
-1	-1	1	-і	і
і	і	-і	-1	1
-і	-і	і	1	-1

Якщо кількість елементів порівняно невелика, то бінарність визначається побудовою таблиці Келлі:

Мультиплікативна абелева група 4 – го порядку.

2. 1 відносно множення. Мультиплікативна абелева група 1-го порядку.

3. сукупність всіх парних чисел відносно додавання. Адитивна абелева група нескінченного порядку.

4. Множина матриць 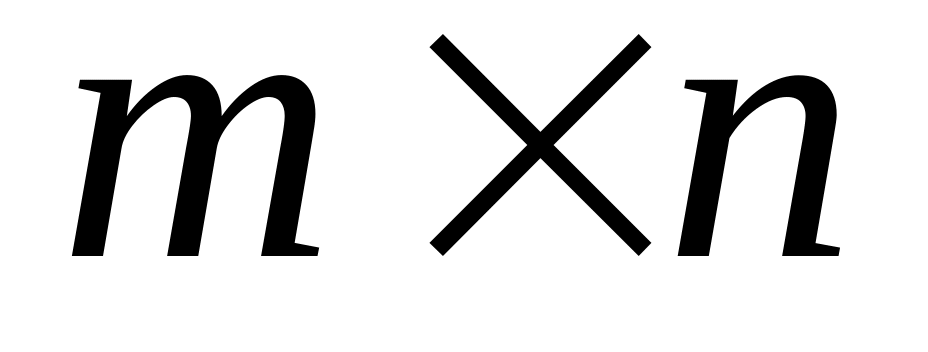відносно додавання.

5. Групою не будуть натуральні числа.

6. Цілі числа утворюють групу.

7. Раціональні числа відносно множення не є групою.

Властивості груп:

1. правий обернений елемент є одночасно і лівим оберненим елементом.

2. правий нейтральний елемент є одночасно і лівим нейтральним елементом.

3. нейтральний елемент в групі єдиний.

4. для будь-яких , існує , що .

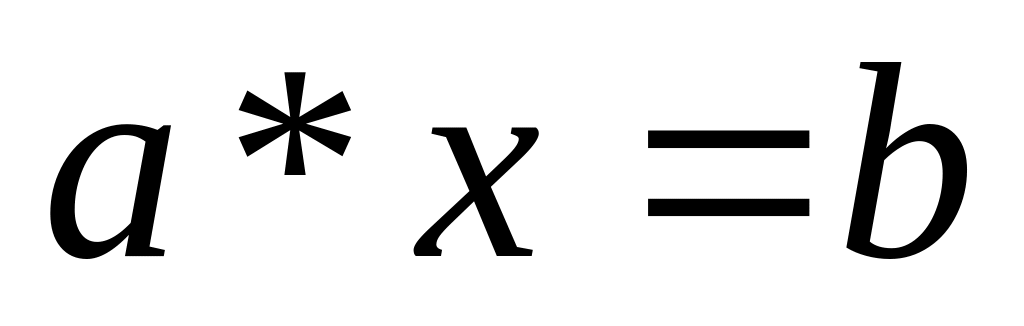- елемент, який співставляється парі , тоді . Якщо визначений , то . Для адитивних груп: і т. д.

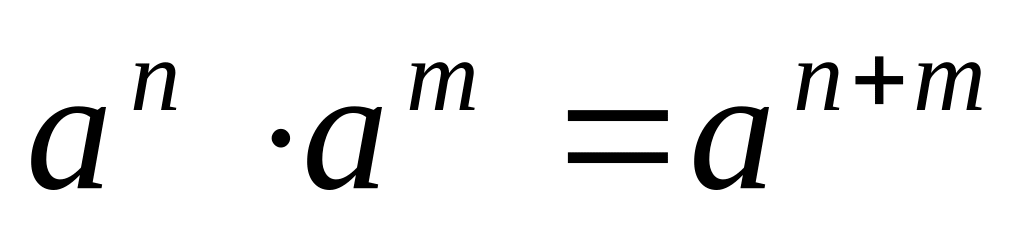5. . 6. .

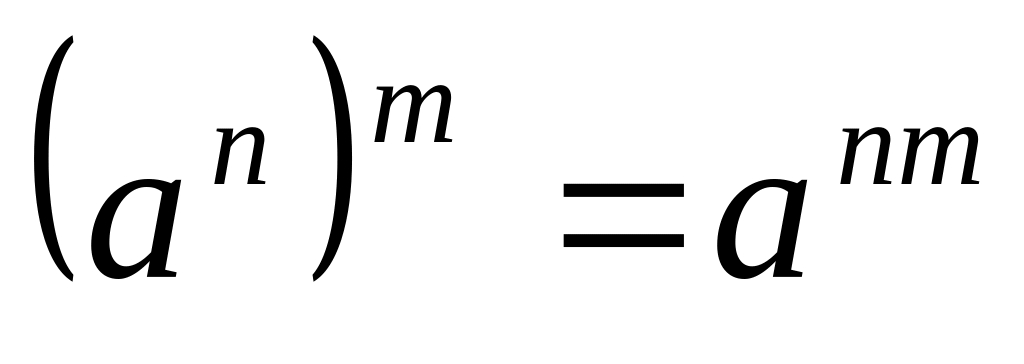Доведемо власт. 3, 4:

3)Методом від супротивного, використовуючи модифікацію: .

Маємо два нейтральних елементи: .

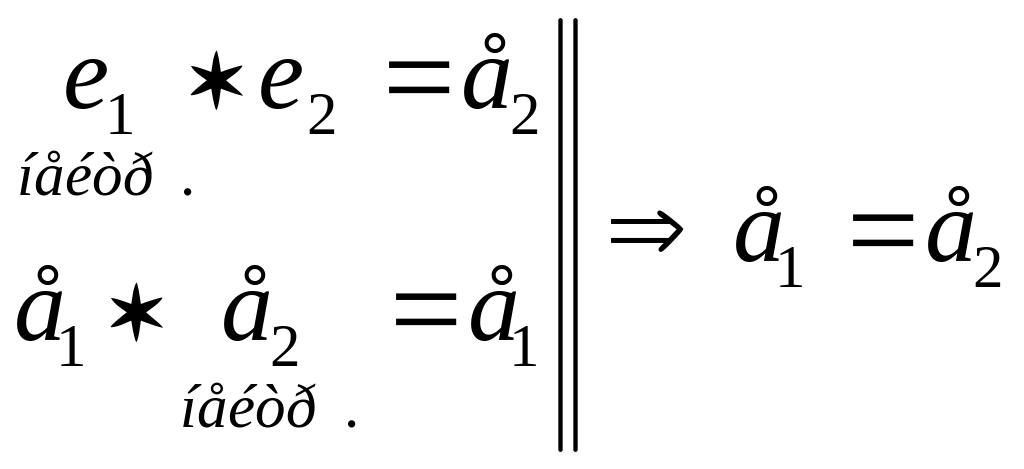4)Покажемо, що є єдиним розв’язком даного рівняння. Підставимо в рівняння: операція асоціативна лівий нейтральний елемент є одночасно правим . Єдність розв’язку випливає із бінарності операції.