
- •Диференціальні рівняння з частинними похідними першого порядку. Звязок з системою звичайних диференціальних рівнянь у симетричній формі.
- •Класифікація диференціальних рівнянь з частинними похідними іі порядку для випадку двох і багатьох незалежних змінних.
- •Види топологічних просторів. Топологія, індукована метрикою.
- •Поняття метричного простору. Простір ізольованих точок. Метричні простори r1, r(n), c[a,b].
- •Граничні точки, точки дотику, замикання множини. Сепарабельні простори. Послідовність в метричному просторі. Границя послідовності.
- •Стискаючі відображення, їх неперервність. Теорема Банаха, її геометричне тлумачення.
- •Поняття лінійного простору. Приклади. Лінійна залежність і лінійна незалежність елементів. Нескінченно - вимірні простори. Підпростори.
- •Означення і приклади нормованих просторів. Означення евклідових просторів. Нерівність Буняковського - Коші.
- •Означення і приклади лінійних операторів. Неперервність і обмеженість. Норма операторів. Сума і добуток операторів. Обернений оператор, оборотність.
- •Бінарні відношення. Рефлексивні, симетричні, транзитивні бінарні відношення. Класи еквівалентності, фактор–множина.
- •Бінарні відношення порядку, його властивості. Мінімальні та максимальні елементи. Впорядковані множини.
- •Групи. Приклади груп. Основні властивості груп.
- •Ізоморфізм та гомоморфізм груп. Його властивості.
- •Кільце, приклади кілець. Основні властивості кілець. Ізоморфізм та гомоморфізм груп
- •Поле. Приклади полів, основні властивості полів. Ізоморфізм та гомоморфізм полів.
- •Поле комплексних чисел. Комплексні числа, алгебраїчна форма комплексних чисел.
- •Неперервні відображення топологічних просторів і їх властивості. Гомеоморфізм.
- •Теорема Ейлера для многогранників.
- •Суть сучасного аксіоматичного методу. Основні вимоги до системи аксіом. Поняття про інтерпретацію системи аксіом.
- •Точково–векторна аксіоматика Вейля трьохвимірного евклідового простору і її несуперечливість.
- •Вимірювання многокутників. Площа многокутника і її аксіоми. Теорема існування і єдиності.
- •Рівноскладеність і рівновеликість многокутників і многогранників.
- •Аксіоматика площини Лобачевського. Абсолютна геометрія. Паралельні напрямлені прямі на площині Лобачевського і їх властивості.
- •Взаємне розміщення прямих на площині Лобачевського. Теорема про існування розбіжних прямих і наслідки з неї. Критерій розбіжності двох прямих.
- •Трикутники на площині Лобачевського.
- •Незалежність аксіоми паралельності від решти аксіом д. Гільберта.
Означення і приклади лінійних операторів. Неперервність і обмеженість. Норма операторів. Сума і добуток операторів. Обернений оператор, оборотність.
Нехай
є два лінійних простори
![]() і
і
![]() .
Якщо кожному елементу
простору
поставлено у відповідність цілком
певний елемент
із простору
,
то кажуть, що заданий оператор
,
який діє у просторі
із
значеннями в
.
.
Якщо кожному елементу
простору
поставлено у відповідність цілком
певний елемент
із простору
,
то кажуть, що заданий оператор
,
який діє у просторі
із
значеннями в
.
Оператор
![]() наз. лінійним,
якщо для
наз. лінійним,
якщо для
![]() і для будь-яких чисел
і для будь-яких чисел
![]() і
і
![]() виконується рівність
виконується рівність
![]() .
Пр.
.
Пр.
![]() .
.
Оператор
діє в просторі
.
Будемо вважати, що
![]() і
- неперервні. Перевіримо умову лінійності:
і
- неперервні. Перевіримо умову лінійності:
![]()
З лінійності оператора випливають властивості:
1.
![]() ;
2.
;
2.
![]() .
.
Лінійний
оператор
наз. неперервним
в точці
,
якщо із збіжності будь-якої послідовності
![]() випливає,
що відповідна послідовність значень
оператора
випливає,
що відповідна послідовність значень
оператора
![]() ,
,
![]() .
Тут збіжність розуміється за нормою
даного простору
,
тоді
.
Тут збіжність розуміється за нормою
даного простору
,
тоді
![]() .
.
Якщо лінійний оператор неперервний в точці , то він неперервний і в довільній точці довільного простору.
Довед.
Розглянемо довільну послідовність
![]() і покажемо, що
і покажемо, що
![]() .
Розглянемо довільний елемент
.
Розглянемо довільний елемент
![]() .
Тоді в силу неперервності в
.
Тоді в силу неперервності в
![]() .
Використаємо лінійність:
.
Використаємо лінійність:
![]() ,
тоді
,
тоді
![]() .
.
Лінійний
оператор, який діє в лінійному просторі
із
значеннями в лінійному просторі
наз. обмеженим,
якщо існує таке число
![]() ,
що для
,
що для
![]() .
.
Теор. Для того, щоб лінійний оператор був неперервним у будь-якій точці , необхідно і достатньо, щоб він був обмеженим.
Доведення.
Необхідність. Дано:
-
неперервний оператор. Доведемо
обмеженість, тобто що
![]() ,
,
![]() .
Припустимо протилежне, оператор
необмежений. Це означає, що для
.
Припустимо протилежне, оператор
необмежений. Це означає, що для
![]()
Розглянемо
елемент
![]() ,
і оцінимо за нормою
,
і оцінимо за нормою
![]() ,
;
,
;
![]() ,
,
,
,
![]() ,
тоді в силу неперервності
,
тоді в силу неперервності
![]() ,
а з іншого боку
,
а з іншого боку
![]() ,
не прямує до нуля,
.
Суперечність.
,
не прямує до нуля,
.
Суперечність.
Достатність.
Дано, що оператор обмежений, тобто
![]() ,
,
![]() .
.
Доведемо,
що для
![]() ,
.
,
.
![]() ;
;
![]() .
.
Нехай маємо лінійний обмежений оператор: , .
Найменша
з компонент
,
яка фігурує в умові обмеженості наз.
нормою
оператора
і позначається
![]() ,
,
![]() .
.
По-іншому,
число
наз. нормою
оператора,
якщо для
![]() ,
,
![]() ,
,
![]() .
.
Приклад.
Маємо
відображення
![]() ,
,
![]() .
.
![]() - фіксований вектор.
- фіксований вектор.
![]() - змінний вектор.
- змінний вектор.
Знайдемо норму оператора
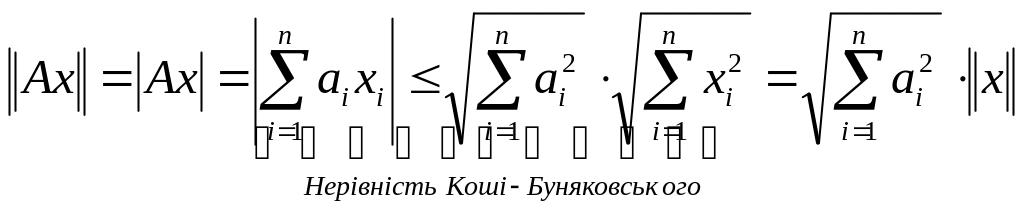 .
.
![]() .
Покажемо, що насправді
рівна правій частині. Для цього достатньо
знайти елемент
,
щоб нерівність перетворювалася б в
рівність. Розглянемо елемент
.
Покажемо, що насправді
рівна правій частині. Для цього достатньо
знайти елемент
,
щоб нерівність перетворювалася б в
рівність. Розглянемо елемент
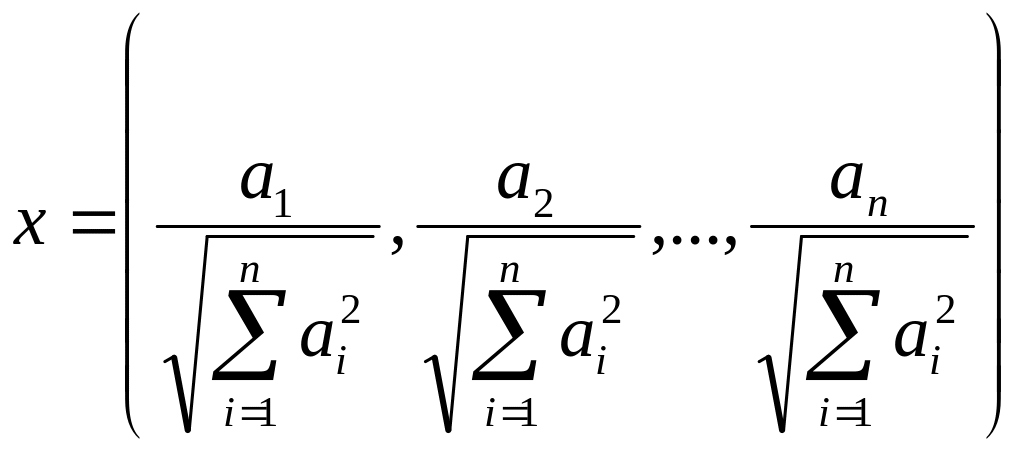 ,тоді:
,тоді:
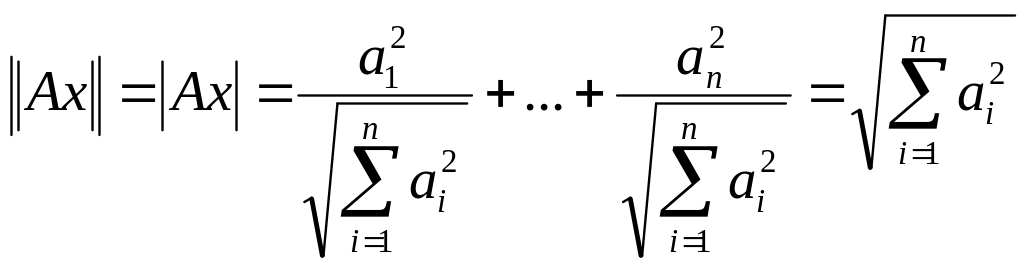 .
.
Бінарні відношення. Рефлексивні, симетричні, транзитивні бінарні відношення. Класи еквівалентності, фактор–множина.
Розглянемо
2-і множини
і
![]() елементів довільної природи.
елементів довільної природи.
Прямим
(декартовим) добутком 2-ох множин
наз. сукупність всіх можливих впорядкованих
пар елементів
![]()
![]() таких, що
таких, що
![]() .
.
Будь-яка
підмножина прямого добутку
![]() наз. бінарним
відношенням.
Бінарні відношення познач. маленькими
грецькими буквами
наз. бінарним
відношенням.
Бінарні відношення познач. маленькими
грецькими буквами
![]() .
.
Бінарне
відношення вважається заданим, якщо
можна встановити чи належить пара
![]() цьому бінарному відношенню. Той факт,
що пара
належить бінарному відношенню
записується так:
цьому бінарному відношенню. Той факт,
що пара
належить бінарному відношенню
записується так:
![]() або
або
![]() (
(![]() перебуває у відношенні
до
перебуває у відношенні
до
![]() ).
).
Якщо
прямий добуток
містить
- елементів, то всіх бінарних відношень
буде
![]() .
.
Бінарні відношення можна задати:
1)Переліком
елементів, які йому належать, 2)Графіком,
3)Стрілками (записуємо множини А і В і
стрілками з’єднуємо ті елементи, які
перебувають і відношенні
).
4)Формулою. Наприклад, функція Діріхле:
![]() ,
5)Словесно, 6)Графом.
,
5)Словесно, 6)Графом.
Властивості бінарних відношень
Розглянемо
прямий добуток
![]() .
.
Бінарне
відношення
,
що визначене на
![]() наз. рефлексивним,
якщо
наз. рефлексивним,
якщо
![]() .
.
Бінарне
відношення
,
що визначене на
наз. симетричним,
якщо
![]() .
.
Бінарне
відношення
,
що визначене на
наз. транзитивним,
якщо
![]() .
.
Крім цих властивостей відношення мають ще такі властивості:
Бінарне
відношення
,
що визначене на
наз. антирефлексивним,
якщо
![]() .
.
Бінарне
відношення
,
що визначене на
наз. антисиметричним,
якщо
![]() .
.
Бінарне відношення , яке є рефлексивним, симетричним, транзитивним наз. відношенням еквівалентності.
Нехай - відношення еквівалентності, яке визначене декартовим добутком . Зафіксуємо в елемент .
Класом еквівалентності з твірним елементом наз. множина елементів з , які перебувають у відношенні до елемента .
![]()
Так як відношення еквівалентності, то воно одночасно і рефлексивне, і симетричне, і транзитивне. Із означення випливають такі властивості:
Кожний елемент належить своєму класу еквівалентності
 .
.Різні класи еквівалентності не перетинаються.
Розбиттям множини наз. така сукупність її підмножин, які не перетинаються і об’єднання яких співпадає з множиною.
Сама сукупність підмножин розбиття наз. фактор – множиною, а процес знаходження множин наз. факторизацією множини.
Таким чином, множина класів еквівалентності є фактор – множиною і є спеціальним розбиттям множини .
