Стискаючі відображення, їх неперервність. Теорема Банаха, її геометричне тлумачення.
Існує
багато теорем пов’язаних з існуванням
кореня розв’язку рівнянь (
,
диференціальних рівнянь, інтегральних,
СЛАР), які можуть бути доведені з єдиної
точки зору: шляхом доведення існування
нерухомої точки деякого відображення.
Точка
наз. нерухомою
точкою відображення метричного простору
в себе, якщо справедливою є рівність
.
Відображення
метричного простору
в себе наз. стискуючим,
або просто стиском,
якщо існує таке число
,
що викон. нерівність:
.
Тобто відстань між образами не перевищує відстань між прообразами.
Теор. Усяке стискуюче відображення є неперервним.
Довед.
Доведення проведемо на мові послідовностей,
тобто за Гейне. Нехай
- довільна послідовність, яка збігається
до елемента
.
Тобто
,
при
.
Запишемо умову стиску:
,
.
При
,
,
отже
,
звідки вираз у лівій частині теж прямує
до нуля, що означає, що послідовність
.
Звідки слідує неперервність відображення.
Теор. Банаха. Усяке стискуюче відображення, яке переводить повний простір в себе, має в цьому просторі одну і тільки одну нерухому точку , або що те саме, що рівняння має єдиний корінь .
Доведення. Дано:
-
повний простір;
-
відображення в себе;
, - стискуюче відображення.
Треба
довести, що існує елемент
,
такий що
.
Нехай - довільна точка з простору . Побудуємо послідовність таким чином:
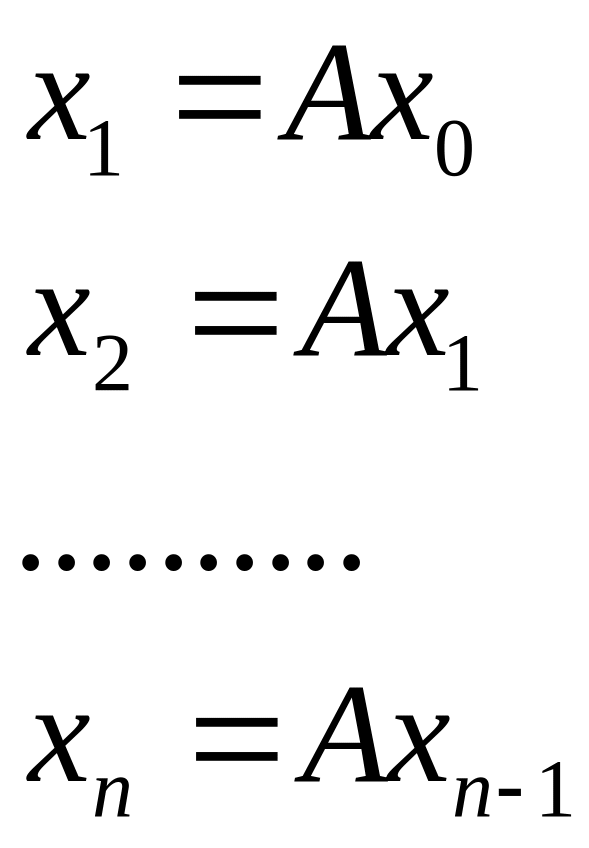
Покажемо,
що така послідовність є фундаментальною,
тобто, що знайдуться такі
,
що
.
Не зменшуючи загальності будемо вважати,
що
.
Оцінимо:
,
коли
.
Невідомою залишається поведінка другого множника. Оскільки простір метричний, то ми можемо використати нерівність трикутника:
Оцінимо кожен
доданок починаючи з другого даної
нерівності:
,
Аналогічно будемо мати:
………………………….
Далі очевидно:
.
Оскільки
,
коли
(як
вже говорилось), а
-
є якась фіксована стала, то і весь вираз
у правій частині при
теж прямує до нуля. Це означатиме, що
наша послідовність є фундаментальною.
Оскільки простір у нас повний, то
фундаментальна послідовність матиме
в йому границю:
.
Покажемо,
що
буде нерухомою точкою відображення,
тобто
.
Маємо:
,
а
.
Відображення А
є неперервним,
отже якщо
при
,
то
буде прямувати до
,
тобто матимемо, що
при
,
що й і означає, що
є
нерухома точка відображення.
Покажемо, що ця
точка єдина. Нехай
,
таке що
,
тоді матимемо, що
.
Отже ми отримали, що :
,
це можливо лише тоді, коли
=0.
Оскільки простір метричний, тоді за
1-ою аксіомою метрики слідує, що
.
Зауваж. 1. В процесі доведення теореми Банаха ми не тільки довели існування нерухомої точки, а й вказали спосіб її наближеного відшукання. Цей метод носить назву методу послідовних наближень. Кінцевий результат не залежить від вибору нульового наближення . Цей факт з обчислювальної точки зору представляє значний інтерес, бо кожне з наступних наближень ми можемо прийняти за , що не дасть накопичуватись похибкам, які будуть залежати від початкового наближення.
Зауваж. 2. На практиці обчислення припиняють на якомусь кроці. Тоді виникає питання, як оцінити похибку між точним результатом і наближеним. Скористаємось нерівністю, яку отримали в процесі доведення теореми:
,
при
матимемо:
.
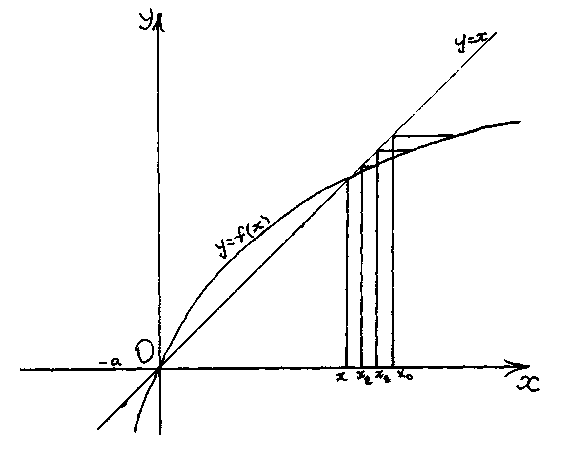
Дамо геометричну ілюстрацію теореми Банаха.
Дана оцінка та графічна ілюстрація показують, що показує, що послідовні наближення збігаються до точного розв’язку із швидкістю геометричної прогресії.
