28. Взаємне розміщення прямих на площині Лобачевського. Теорема про існування розбіжних прямих і наслідки з неї. Критерій розбіжності двох прямих.

На площині Лобачевського, на відміну від площини Евкліда мають місце три випадки взаємного розташування двох прямих: прямі перетинаються, паралельні або розбігаються.

Дві прямі на площині Лобачевського наз. розбіжними (або надпаралельними), якщо вони не перетинаються і не паралельні. Легко побачити, що через кожну точку М, яка не лежить на прямій а, проходить нескінчена множина прямих, кожна з яких розбігається з прямою а. Насправді, нехай прямі С та Е паралельні до прямої а в різних напрямках. Тоді будь-яка пряма, що проходить через точку М в середині вертикальних кутів СМ та ЕМ , розбігається з прямою а.

Теор. Дві прямі, що мають спільний перпендикуляр, розбігаються. Нехай АВ та С - дані прямі, а Р - їх спільний перпендикуляр. Як відомо, прямі АВ та С не перетинаються. Вони не можуть бути паралельними, так як якщо припустити, що вони паралельні, то прямі кути АР та повинні бути кутами паралельності в точці Р відносно прямої С . Але кут паралельності завжди гострий, тому наше припущення не вірне: значить, АВ та С - прямі що розбігаються.

Наслідок 1. На площині Лобачевського не існує спільного перпендикуляра двох паралельних прямих.

Н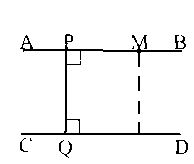 ехай АВ і - розбіжні прямі, а Р спільний перпендикуляр цих прямих (рис. 2). Відстань від змінної точки М прямої АВ до прямої С необмежено зростає, коли точка М віддаляється від точки Р як в одному, так і в іншому напрямку.

рис. 2

Тобто, розбіжні прямі необмежено "розбігаються" одна від іншої по мірі віддалення від спільного перпендикуляра.

Нехай тепер А В // С , а Р - перпендикуляр, проведений з точки Р прямої АВ на пряму С (рис. 3). Так як РВ гострий, то суміжний з ним РА тупий. Відстань від змінної точки М прямої АВ до прямої С необмежено зростає, коли точка М віддаляється від точки Р в сторону, обернену до напрямку паралельності. Можна довести, що якщо точка М віддаляється від точки в сторону паралельності, то ця відстань наближається до нуля. Образно кажучи, паралельні прямі, необмежено віддаляючись одна від іншої в одному напрямку, асимптотично наближаються в іншому.

Наслідок 2. Якщо при перетині двох прямих і третьою прямою будь-які два відповідні кути рівні, то прямі розбігаються.

29. Трикутники на площині Лобачевського.

Всі теореми при трикутники, які в евклідовій геометрії .доводяться, без допомоги аксіоми паралельності мають місце також в геометрії. Лобачевського. Теореми про рівнобедрений трикутник, три ознаки рівності трикутників, теорема про зовнішній кут трикутника - це далеко не повний перелік теорем, які мають місце як в евклідовій геометрії, так і в геометрії Лобачевського.

Але трикутники на площині Лобачевського мають специфічні властивості. Розглянемо деякі з них.

Теор:. Сума кутів будь-якого трикутника менше 2d.

Нехай АВС - довільний трикутник. За першою теоремою Саккері-Лежандра . Якщо припустити, що , тоді буде справедливий V постулат. Отже, .

Наслідок. Сума кутів трикутника не стала, тобто не одна й та ж для всіх трикутників.

Н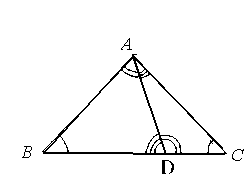 ехай АВС - довільний трикутник, а - точка яка належить стороні ВС Простий підрахунок показує, що (рис. 1). Так як , то .

Доведемо ще одну важливу теорему, згідно якої в геометрії Лобачевского відсутнє поняття подібності трикутників.

Теор.(четверта ознака рівності трикутників): Трикутник рівний трикутнику , якщо

Рис.1

Ще одна властивість трикутників аналогів якої немає в евклідовій геометрії.

Теор.: На площині існують трикутники навколо яких не можна описати коло.

Довед. Для доведення теореми достатньо показати хоча б один приклад такого трикутника. Так як і в евклідовій геометрії центр описаного кола лежить на перетині перпендикулярів, проведених через середини сторін.

Візьмемо дві паралельні прямі та . Із точки прямої опустимо перпендикуляр на пряму . Нехай - основа перпендикуляра. Візьмемо на відрізку довільну точку і побудуємо симетричні точки та відносно прямих та . Точки , і не лежать на одній прямій. Таким чином, ми побудували трикутник , для якого перпендикуляри, проведені через середини сторін та , не перетинаються. Це означає, що навколо трикутника не можна описати коло.