24. Точково–векторна аксіоматика Вейля трьохвимірного евклідового простору і її несуперечливість.

Основними об’єктами в системі аксіом Вейля є точка і вектор. Основними співвідношеннями між об’єктами є

• Сума 2-ох векторів: .

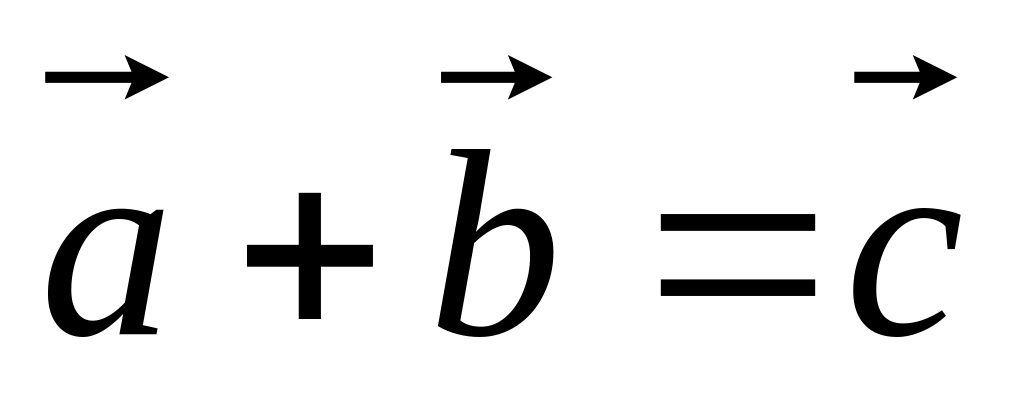• Добуток вектора на скаляр.

• Для будь-яких двох векторів визначена операція скалярного добутку: .

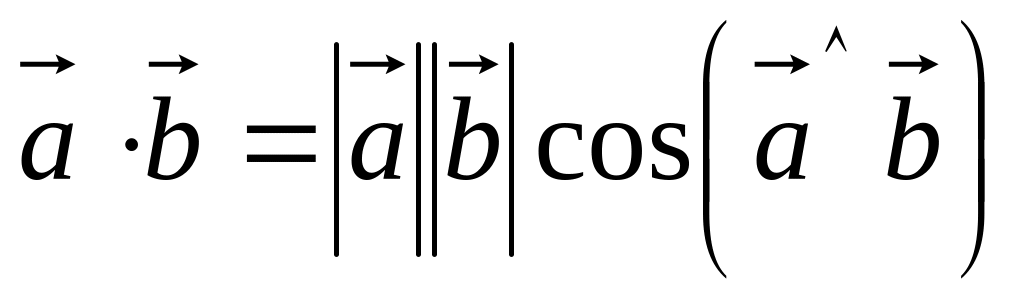• Будь-які дві різні точки та визначають вектор .

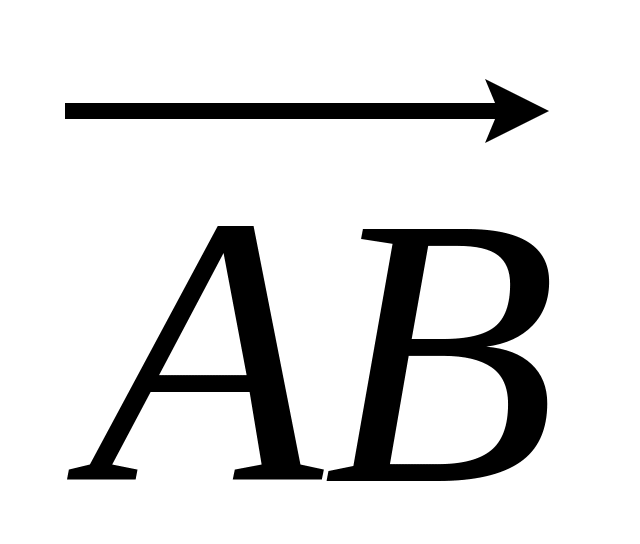Вказані вище співвідношення за Вейлем задовольняють таким умовам (аксіомам):

1. Аксіоми лінійного векторного простору

. Для будь-якого вектора ,

. Для будь-якого вектора ,

. Для будь-яких 2-ох векторів і виконується закон комутативності: .

. Для будь-яких 3-ох векторів , і виконується асоціативний закон: ,

. Для будь-якого вектора ,

. Для будь-якого вектора і , із виконується закон дистрибутивності відносно додавання скалярів ,

. Для будь-якого вектора і , із .

. Для будь-яких 2-ох векторів , і із виконується закон дистрибутивності відносно додавання векторів .

2. Аксіоми розмірності

. В просторі існує три лінійно незалежних вектори, тобто із .

. Всякі чотири вектори у просторі є лінійно залежними, тобто із .

3. Аксіоми скалярного добутку.

. Для будь-яких 2-ох векторів і маємо ,

. Для будь-яких 2-ох векторів і маємо .

. Для будь-яких 3-ох векторів , і .

. Для будь-якого вектора маємо .

4. Аксіоми належності

. В просторі існує принаймні одна точка.

. Для будь-якої точки та будь-якого вектора існує єдина точка така, що .

. Для будь-яких 3-ох точок , і виконується векторна рівність .

Несуперечливість системи аксіом Вейля.

Для доведення несуперечливості системи аксіом Вейля побудуємо її модель та перевіримо виконання на ній аксіом Вейля.

Під точкою розумітимемо таку матрицю і , де , якщо .

Під вектором будемо розуміти таку матрицю 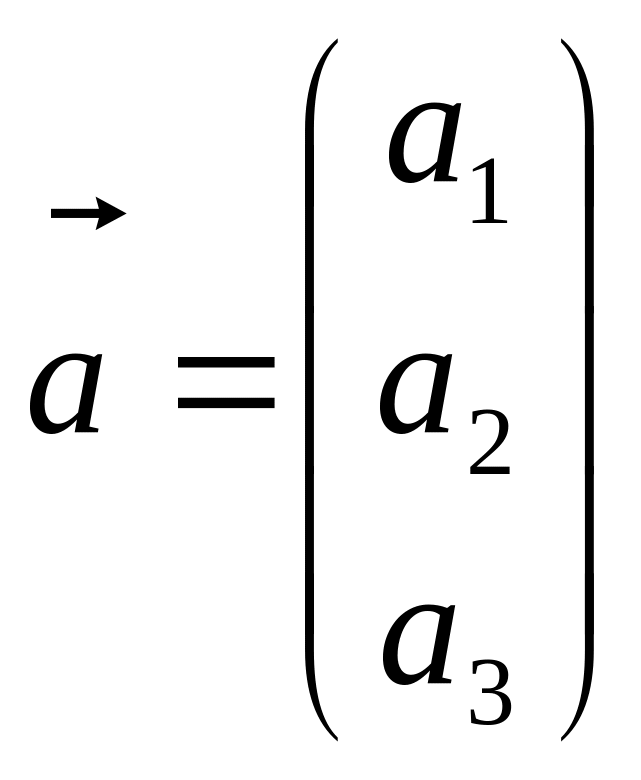і якщо , то , якщо .

Під сумою розумітимемо таку матрицю .

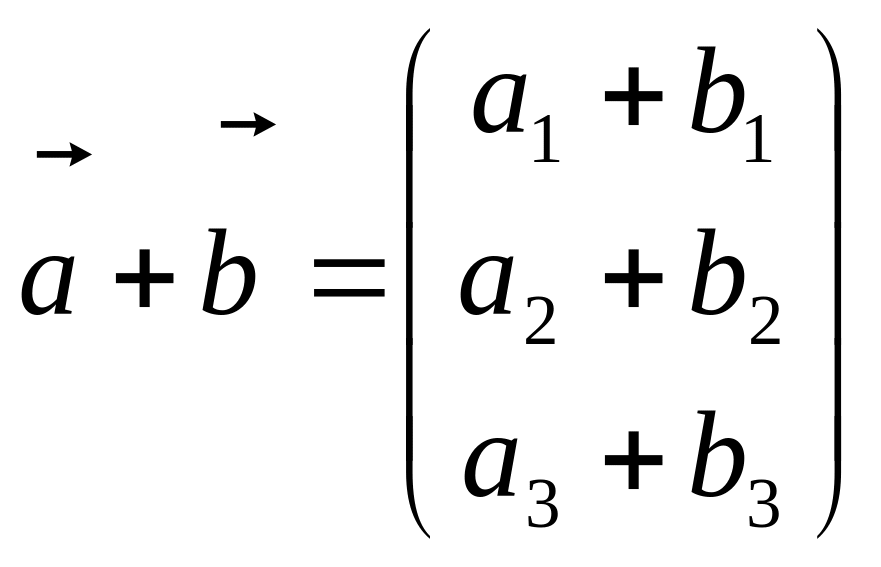Під множенням на скаляр розумітимемо матрицю .

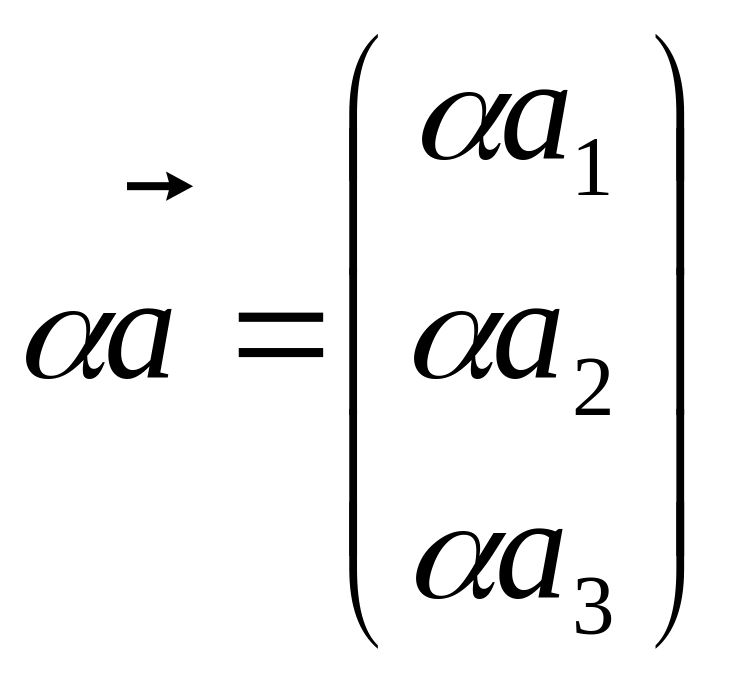Під скалярним добутком будемо розуміти число, яке визначається так .

Під дві точки визначають вектор . Перевіримо виконання аксіом:

.

. ,

. .

. ,

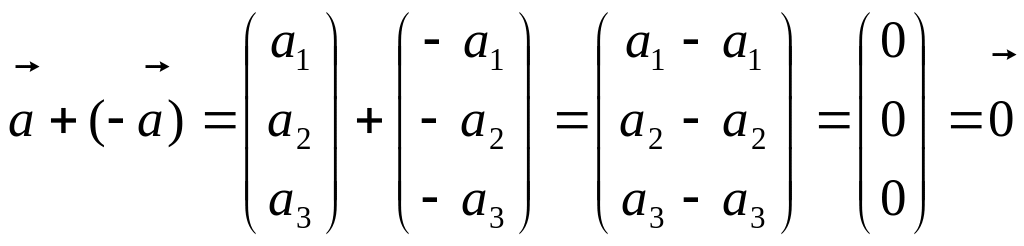і т.д.

. Виберемо три вектори , , 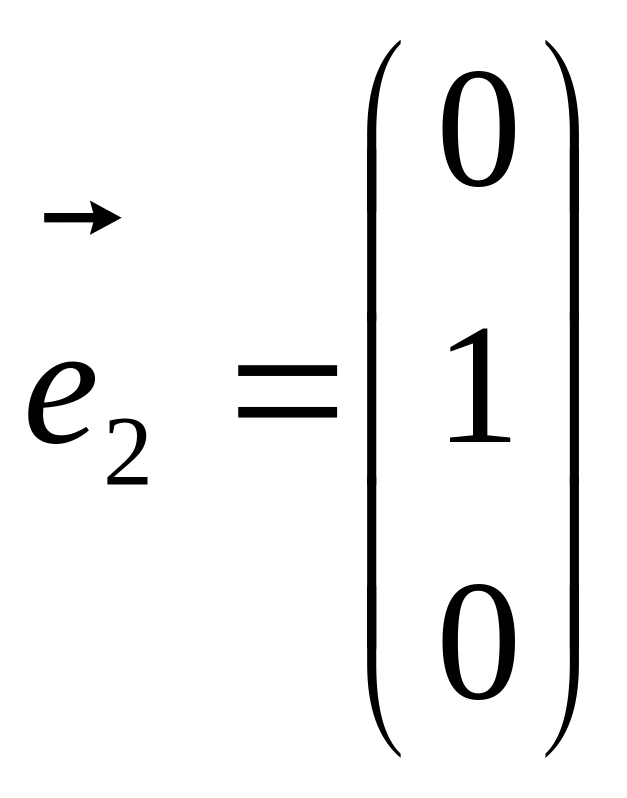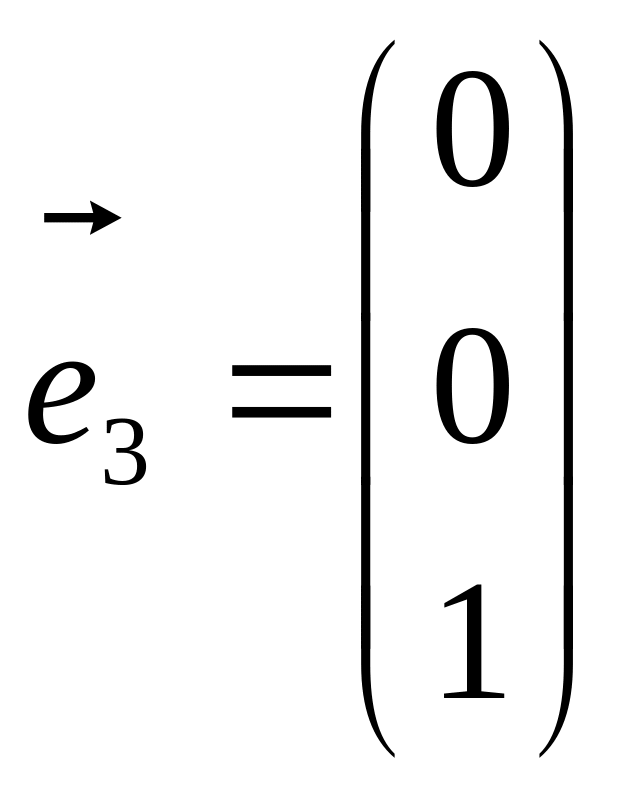. Розглянемо лінійну комбінацію: , якщо , то вони лінійно незалежні 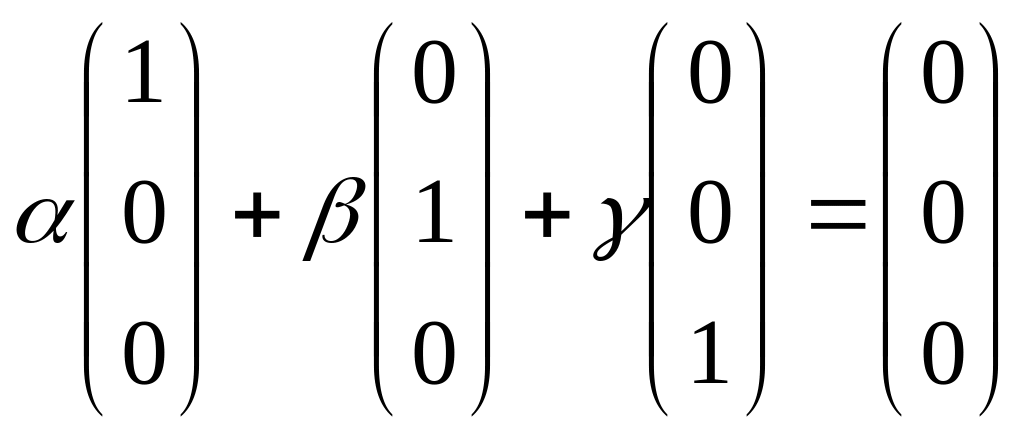. Рівні вектори мають рівні відповідні координати.

, ,

, ,

, . Отже, вектори лінійно незалежні.

і т.д.

. .

Таким чином доводиться несуперечність аксіом Вейля.

25. Вимірювання многокутників. Площа многокутника і її аксіоми. Теорема існування і єдиності.

Розглянемо - точок загального положення (кожні три не лежать на одній прямій). Сполучимо їх відрізками. - вершини ламаної, сторони ланки.

Якщо всі точки ламаної лежить на площині, то маємо плоску ламану. Якщо перша і остання вершини збігаються, то наз. її плоскою замкненою кривою. Замкнена ламана розбиває площину на зовнішню і внутрішню області.

Об’єднання плоскої замкненої лінії з її внутрішньої

області наз. плоским многокутником. Плоский много-

кутник наз простим, якщо всі його вершини різні, жодна

не належить стороні і ніякі дві з них не перетинаються.

Покажемо, що на множині простих многокутників

можна ввести поняття «вимірювання многокутників»,

тобто покажемо, що кожному многокутнику можна

поставити у відповідність скалярну величину – площу

многокутника, яка задовольняє такі умови (аксіоми площі):

• Площа є величиною додатною,

• Рівні многокутники мають рівні площі,

• Площа суми многокутників дорівнює сумі площ даних многокутників,

• Площа квадрата, довжина сторони якого дорівнює 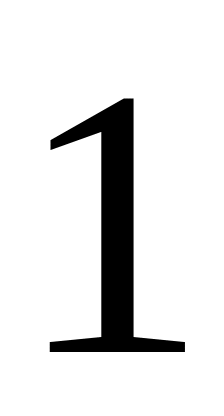, дорівнює одиниці.

Введемо поняття орієнтованого многокутника. Многокутник наз. орієнтовним, якщо вказано порядок обходу його вершин, причому проти годинникової стрілки вважають додатньо орієнтовним, а за – від’ємно орієнтовним. Многокутник – неорієнтований, – орієнтовним.

Розглянемо поняття характеристики орієнтованого многокутника. Для цього введемо афінну систему координат.

Кожна точка має координати , ,

,…, .

Характеристикою орієнтованого многокутника

наз. величина, яка дорівнює

, де

.

Наприклад, розглянемо трикутник :

.

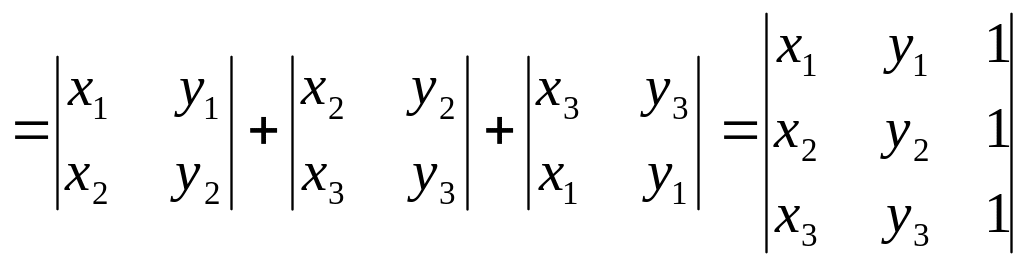Помістимо трикутник вершину в точку : , , .

.

Тепер в системі координат розглянемо квадрат : , , , .

. Якщо , то .

( ) ( )

Теорема: Якщо за площу орієнтованого многокутника прийняти половину модуля його характеристики, то будуть виконуватись всі чотири аксіоми площі.