
- •Диференціальні рівняння з частинними похідними першого порядку. Звязок з системою звичайних диференціальних рівнянь у симетричній формі.
- •Класифікація диференціальних рівнянь з частинними похідними іі порядку для випадку двох і багатьох незалежних змінних.
- •Види топологічних просторів. Топологія, індукована метрикою.
- •Поняття метричного простору. Простір ізольованих точок. Метричні простори r1, r(n), c[a,b].
- •Граничні точки, точки дотику, замикання множини. Сепарабельні простори. Послідовність в метричному просторі. Границя послідовності.
- •Стискаючі відображення, їх неперервність. Теорема Банаха, її геометричне тлумачення.
- •Поняття лінійного простору. Приклади. Лінійна залежність і лінійна незалежність елементів. Нескінченно - вимірні простори. Підпростори.
- •Означення і приклади нормованих просторів. Означення евклідових просторів. Нерівність Буняковського - Коші.
- •Означення і приклади лінійних операторів. Неперервність і обмеженість. Норма операторів. Сума і добуток операторів. Обернений оператор, оборотність.
- •Бінарні відношення. Рефлексивні, симетричні, транзитивні бінарні відношення. Класи еквівалентності, фактор–множина.
- •Бінарні відношення порядку, його властивості. Мінімальні та максимальні елементи. Впорядковані множини.
- •Групи. Приклади груп. Основні властивості груп.
- •Ізоморфізм та гомоморфізм груп. Його властивості.
- •Кільце, приклади кілець. Основні властивості кілець. Ізоморфізм та гомоморфізм груп
- •Поле. Приклади полів, основні властивості полів. Ізоморфізм та гомоморфізм полів.
- •Поле комплексних чисел. Комплексні числа, алгебраїчна форма комплексних чисел.
- •Неперервні відображення топологічних просторів і їх властивості. Гомеоморфізм.
- •Теорема Ейлера для многогранників.
- •Суть сучасного аксіоматичного методу. Основні вимоги до системи аксіом. Поняття про інтерпретацію системи аксіом.
- •Точково–векторна аксіоматика Вейля трьохвимірного евклідового простору і її несуперечливість.
- •Вимірювання многокутників. Площа многокутника і її аксіоми. Теорема існування і єдиності.
- •Рівноскладеність і рівновеликість многокутників і многогранників.
- •Аксіоматика площини Лобачевського. Абсолютна геометрія. Паралельні напрямлені прямі на площині Лобачевського і їх властивості.
- •Взаємне розміщення прямих на площині Лобачевського. Теорема про існування розбіжних прямих і наслідки з неї. Критерій розбіжності двох прямих.
- •Трикутники на площині Лобачевського.
- •Незалежність аксіоми паралельності від решти аксіом д. Гільберта.
Неперервні відображення топологічних просторів і їх властивості. Гомеоморфізм.
Пригадаємо найпростіше визначення пов’язане з відображенням.
Нехай X
і Y
– довільні множини, а
![]() (1) відображ. множини X
на множину Y.
(1) відображ. множини X
на множину Y.
Позначимо через
![]() множину образів всіх точок множини X.
Очевидно
множину образів всіх точок множини X.
Очевидно
![]() .
.
Якщо
![]() ,то
,то
![]() наз. відображення
множини X
на множину Y.
наз. відображення
множини X
на множину Y.
Відображення
множини X
на множину Y
наз. взаємнооднозначним,
якщо різні точки переходять при цьому
відображенні в різні точки. Очевидно,
що взаємнооднозначне відображення (1)
допускає оборотність, тобто існує єдине
відображення
![]() таке, що
таке, що
![]() і
і
![]() ,
де
,
де
![]() і
і
![]() – тотожні відображення множин X
і Y.
– тотожні відображення множин X
і Y.
Відображення
![]() називається
оборотним
для
і записується
називається
оборотним
для
і записується
![]() .
.
Нехай (1) – дане відображення, а N – підмножина множини Y.
Повним прообразом множини N будемо наз. множину всіх точок в X , образи яких при відображенні (1) містяться в N.
Зауважимо, що повний прообраз множини може бути пустою множиною.
Якщо М
– точка, то її новий прообраз може бути
пустою множиною, однією точкою і множиною,
що складається більше як з однієї точки.
Приведенням
відображ. (1)
наз. таке відображення
![]() ,
яке визначається так: при будь-якому
,
яке визначається так: при будь-якому
![]() маємо
маємо
![]() .
Очевидно, якщо
= Y,
то відображення
і
.
Очевидно, якщо
= Y,
то відображення
і
![]() співпадають.
співпадають.
Нехай дано
відображення (1) і множина
![]() .
Відображення
.
Відображення
![]() наз. звуження
відображення
(1), якщо для всіх
наз. звуження
відображення
(1), якщо для всіх
![]() маємо
маємо
![]() .
.
В топології важливу
роль відіграє неперервне відображення,
яке визначається так: Нехай X
і Y
– топологічні простори. Відображення
(1) наз. неперервним
в
,
якщо для кожного околу
![]() площини
площини
![]() існує
такий окіл
існує
такий окіл
![]() точки
,
що
точки
,
що
![]() .
.
Відображення (1) наз. неперервним на множині , якщо воно неперервне в кожній точці множини М.
Відображення (1) наз. неперервним, якщо воно неперервне на множині X.
Теор.: Для того, щоб відображення (1) було неперервним, необхідно і достатньо, щоб повний прообраз будь якої відкритої множини був множиною відкритою.
Доведення: Нехай
(1) – неперервне відображення.
![]() -- довільна відкрита множина в Y,
а N
– її повний прообраз. Доведемо, що N
– відкрита множина.
-- довільна відкрита множина в Y,
а N
– її повний прообраз. Доведемо, що N
– відкрита множина.
Необх. Для цього
достатньо показати, що кожна точка цієї
множини є внутрішньою. Оскільки
![]() ,
то
– окіл точки
.
В силу неперервності відображ. (1) існує
окіл
точки
x, такий,
що
.
Звідси
,
що
,
то
– окіл точки
.
В силу неперервності відображ. (1) існує
окіл
точки
x, такий,
що
.
Звідси
,
що
![]() ,
а значить x
– внутрішня
точка.
,
а значить x
– внутрішня
точка.
Достат. Нехай x
– довільна точка множини X,
- образ цієї точки, а
- будь який окіл точки
.
Якщо
- повний образ множини
![]() ,
то
відкрита
множина.
,
то
відкрита
множина.
Очевидно, - окіл точки x, крім того . Отже, відображ. (1) неперервне в точці x.
Наслідок. Для того, щоб відображення (1) було неперервним, необхідно і достатньо, щоб повний прообраз будь якої замкненої множини був множиною замкненою.
На основі теореми легко доводяться наступні твердження:
Нехай X, Y, Z – топологічні простори. Якщо і
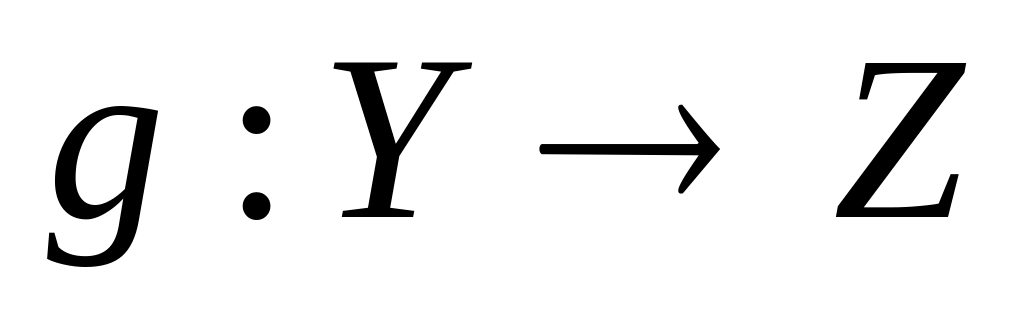 неперервні, то
неперервні, то
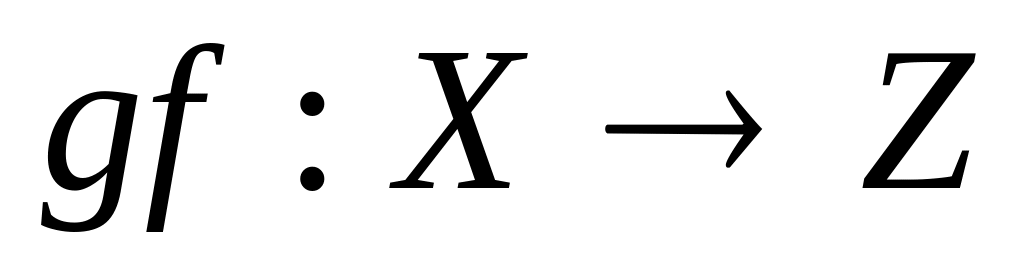 – неперервне.
– неперервне.Якщо відображення (1) неперервне, то для будь якої M
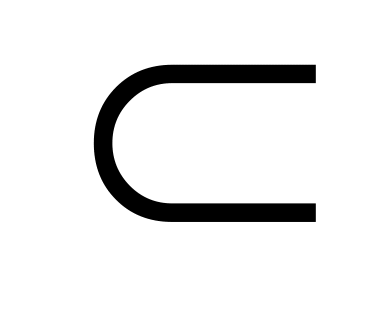 X
відображення
X
відображення
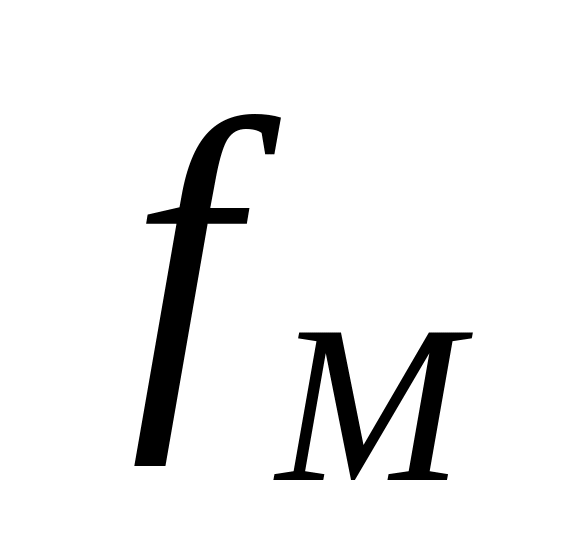 :M
:M Y-
неперервне. Це випливає з (1), якщо
враховувати, що fМ
= fe,
де e:
Y-
неперервне. Це випливає з (1), якщо
враховувати, що fМ
= fe,
де e:
 відображення, при якому образ кожної
точки із М співпадає із самою точкою.
відображення, при якому образ кожної
точки із М співпадає із самою точкою.Приведення
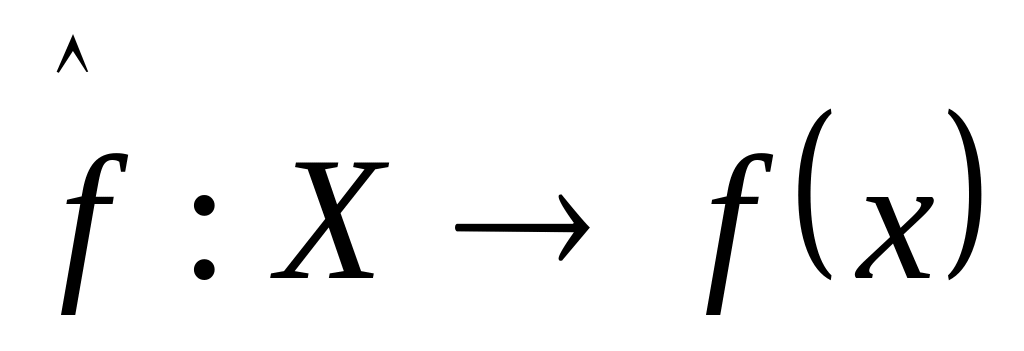 відображення (1) неперервне тоді і тільки
тоді, коли відображення (1) неперервне.
відображення (1) неперервне тоді і тільки
тоді, коли відображення (1) неперервне.
Нехай
![]() -
відображення при якому образ кожної
точки із
-
відображення при якому образ кожної
точки із
![]() співпадає з самою точкою. Очевидно, що
співпадає з самою точкою. Очевидно, що
![]() ,
тому якщо
неперервне, то з (1) слідує, що
- неперервне. Обернене твердження
очевидне.
,
тому якщо
неперервне, то з (1) слідує, що
- неперервне. Обернене твердження
очевидне.
Нехай Х
і У–тополог.
простори. Відображ. (1) простору Х
на простір У
наз. топологічним,
якщо воно взаємнооднозн. і крім того
відображ.
і
-1
:![]() неперервні.
неперервні.
Топологічні відображення точок наз. гомеоморфізмами (назва від грецьких слів «омео» - однаковий і «морф»- форма. Приклади гомеоморфізмів:
1) тотожнє відображ.
![]() при якому кожна точка множини Х переход.
сама в себе.
при якому кожна точка множини Х переход.
сама в себе.
2) Нехай Х
та У
– числові інтервали,
![]() ,
,
![]()
![]() ,
де a
і b
– дійсні числа,
,
де a
і b
– дійсні числа,
![]() .
Очевидно х,
у
– метричні простори, значить тотожні.
Легко перевірити, що відображення у
= (b-a)х + а є
топологічним. З поняття гомеоморфізму
слідує:
.
Очевидно х,
у
– метричні простори, значить тотожні.
Легко перевірити, що відображення у
= (b-a)х + а є
топологічним. З поняття гомеоморфізму
слідує:
Якщо відображ. є тополог., то відображ.
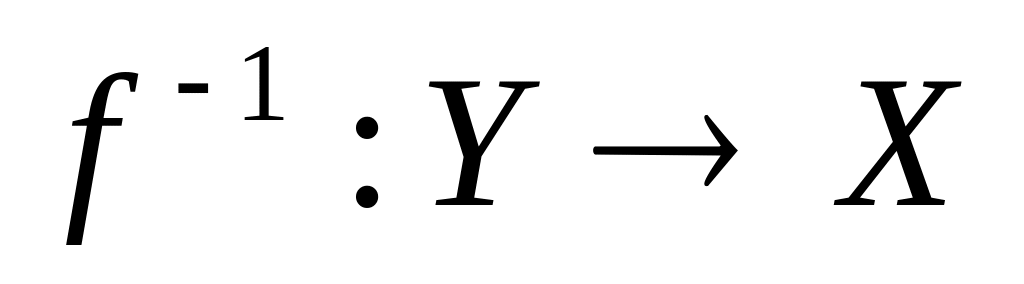 також є
тополог.
також є
тополог.Якщо і є гомеоморфізмами, то є гомеоморфізмом.
Топологічний простір Х наз. гомеоморфним топологічному простору Y, якщо існує такий гомеоморфізм, при якому Х переходить в Y.
Із властивостей 1,2 слідує, що відношення гомеоморфності топологічних просторів рефлексивне, симетричні і транзитивне, тобто є відношенням еквівалентності.
Поняття гомеоморфізму
легко може бути застосованим на множині
точок, що належать топологічним просторам.
Нехай R1
і R2
– топологічні простори, а
![]() ,
,
![]() - довільні множини точок цих просторів.
- довільні множини точок цих просторів.
Відображ. (1) наз
неперервним
в точках х,
якщо для будь якого околу
точки
в R2
існує окіл
![]() точки х
в R1
такий, що
образи всіх точок з
точки х
в R1
такий, що
образи всіх точок з
![]() належать околу
.
належать околу
.
Відображ. (1) наз. неперервним, якщо воно неперервне в усіх точках множини Х.
Взаємнооднозначне відображення (1) множини Х на множину Y наз. топологічним або гомеоморфним, якщо відображення (1) і неперервні.
Якщо існує
гомеоморфізм множини Х на множину Y, то
множини Х та Y наз. гомеоморфічними.
Щоб з’ясувати чи дві множини гомеоморфні,
достатньо знайти хоча б одне топологічне
відображення Х на Y. Якщо, наприклад, при
топологічному відображенні
![]() маємо
маємо
![]() ,
то Х
і Y
гомеоморфні.
,
то Х
і Y
гомеоморфні.
Складніше з’ясувати, що дві множини негомеоморфні. Тут бувають корисними топологічні інваріанти.
Топологічним інваріантом (тополог. властивістю) наз. будь-яку властивість, інваріантну відносно будь-якого топологічного відображення.
Властивість множини бути відкритою (або замкнутою) є топологічний інваріант.
Якщо у множини Х деякий топологічний інваріант присутній, а у множини Y той же інваріант відсутній, то множини Х і Y не можуть бути гомеоморфним.
Гомеоморфні множини топологічно інваріантні, з точки зору топології вони не відрізняються одна від одної. Топологічні перетворення (відображення на себе) множини R очевидно утворюють групу.
