34. Системы передачи с шумоподобными сигналами. Разделение сигналов по форме. Системы со свободным доступом к каналу связи.
В CDMA (Code Division Multiple Access), для каждого узла выделяется весь спектр частот и всё время. CDMA использует специальные коды для идентификации соединений. [1] Каналы трафика при таком способе разделения среды создаются посредством применения широкополосного кодо-модулированного радиосигнала — шумоподобного сигнала, передаваемого в общий для других аналогичных передатчиков канал, в едином широком частотном диапазоне. В результате работы нескольких передатчиков эфир в данном частотном диапазоне становится ещё более шумоподобным. Каждый передатчик модулирует сигнал с применением присвоеного в данный момент каждому пользователю отдельного числового кода, приёмник, настроенный на аналогичный код, может вычленять из общей какофониирадиосигналов ту часть сигнала, которая предназначена данному приёмнику. В явном виде отсутствует временное или частотное разделение каналов, каждый абонент постоянно использует всю ширину канала, передавая сигнал в общий частотный диапазон, и принимая сигнал из общего частотного диапазона. При этом широкополосные каналы приёма и передачи находятся на разных частотных диапазонах и не мешают друг другу. Полоса частот одного канала очень широка, вещание абонентов накладывается друг на друга, но, поскольку их коды модуляции сигнала отличаются, они могут быть дифференцированы аппаратно-программными средствами приёмника.
35. Принципы разделения частотно-временной области. Частотно-временная матрица.
36. Разложение сигналов в базис функций Уолша. Большое значение ряды Фурье приобрели в теории фильтрации, а именно в цифровой фильтрации особенно развиваемой в настоящее время.
Значительному распространению цифровой фильтрации способствовали интенсивные разработки, ведущиеся с конца шестидесятых годов в области применения так называемых быстрых алгоритмов для реализации дискретного преобразования Фурье (ДФП), основанного на специальных ортонормальных системах функций, в частности, на системе функций Уолша.
Базисная система функций {(n(х)} называется ортогональной на отрезке [а,b], если ее элементы удовлетворяют условию
(2.1)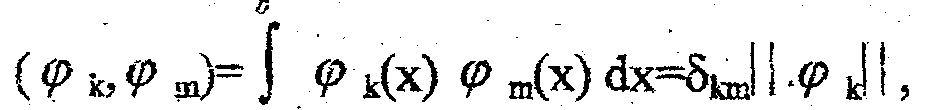
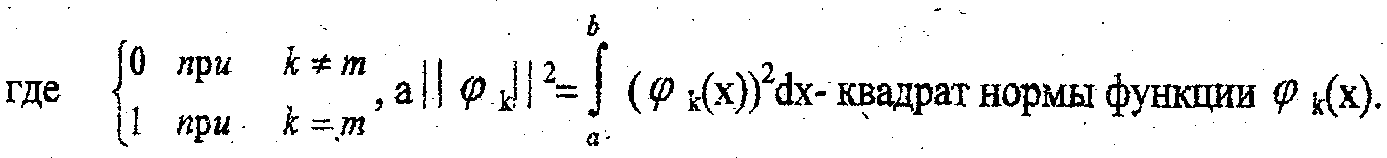
Аппроксимация
сигнала f(х) ортогональным многочленом
при фиксированном числе членов ряда
обеспечивает наилучшее приближение
при минимуме среднеквадратичной ошибки.
Система
функций Уолша является полной
ортонормированной системой на интервале
[0, 1] и может служить базисом спектрального
сигнала.
Любую
интегрируемую на интервале
функцию f(),
являющуюся математической моделью
электрического сигнала, можно представить
рядом Фурье по системе функций Уолша
(2.7)
(2.6)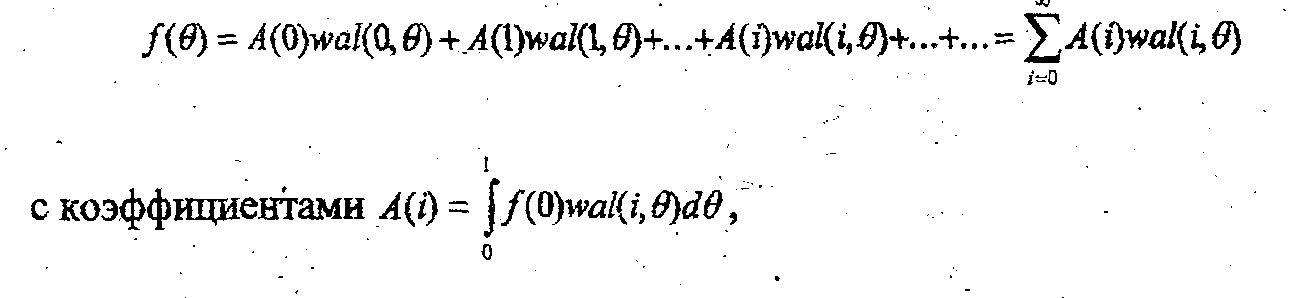
где =t/T - безразмерное время, т.е. время, нормированное к произвольному интервалу времени Т. В реальных расчетах при синтезе и анализе сигналов бесконечный ряд (2.6) заменяется на конечный ряд
где - погрешность аппроксимации. Относительную среднеквадратичную погрешность аппроксимации сигнала f() конечным числом функций Уолша можно определить по формуле
