16. Сигнал с ограниченным спектром. Дискретизация на основе теоремы Котельникова. Функция отсчетов Котельникова.

Д ля восстановления непрерывного сигнала по конечному числу отсчетов решают задачу предельной дискретизации.

Теорема Котельникова: определение частоты квантования для функции с ограниченным спектром.

Непрерывная функция времени, которая не содержит частот в спектре выше некоторой частоты F_в, полностью определяется конечным числом мгновенных значений x(k,Δt), точек отстоящих друг от друга на интервал времени Δt<=1/2F_в.

Теорема Котельникова позволяет представить любую функцию x(t) в виде суммы бесконечного ряда: _, φ_k(t) – функция Котельникова. , где ω_в связана с F_в: ω_в=2π F_в. Sinx/x - для нее φ_k(t)=1.

,

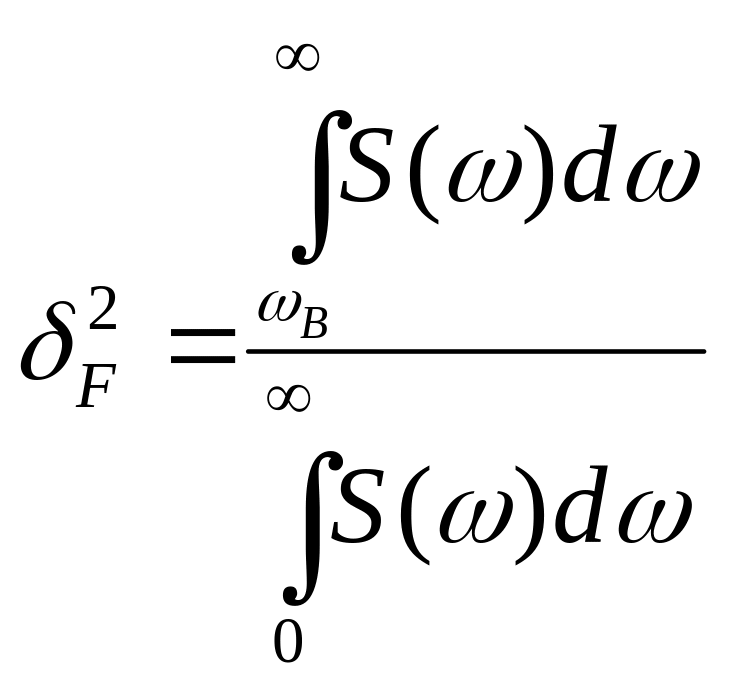
Т – длительность временного интервала, на котором происходит замена функции на множество отсчетов.

N=T/Δt – количество отсчетов (число степеней свободы восстанавливания функции).

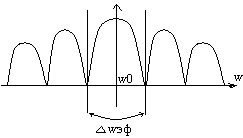
, где - среднеквадратическая ошибка дискретизации; - ошибка связанная с ограничением спектра сигнала частотой ω_в. При дискретизации спектральная функция получаемого сигнала будет периодической функцией, имеющей лепестковую структуру. Важным условием является непересечение «соседних» спектральных составляющих, что обеспечиваеися при соблюдении условий теоремы Котельникова.

17. Количество информации. Энтропия. Свойства энтропии. Измерение количества

информации. Энтропия количества информации.

Формула Хартли: I=log₂N. Имеется n равновероятных сообщений. С помощью некоторого алфавита и дискретного передатчика, необходимо передавать текст сообщения. Слово из n малых букв, N – количество букв алфавита. Тогда число всех возможных слов равно Nⁿ, в результате, I=log₂Nⁿ=n*log₂N. Формула Хартли является случаем синтаксического подхода к случаю измерения количества информации. Формула Шеннона является случаем вероятностного подхода к измерению количества информации или семантического. Для общего случая по Шеннону, если источник сообщения имеет конечное число состояний А₁,А₂,…,А_н, с соответствующими вероятностями Р₁,Р₂,…,Р_н. Тогда энтропия источника: Н(А)=Н(Р₁,Р₂,…,Р_н)= Энтропия – мера неопределенности источника нашего знания о состоянии источника. Количество информации о некотором объекте есть разность между априорной и апостериорной энтропии: I=H_apr-H_aposter. До наблюдения сигнала, несущего информацию об объекте известно только распределение вероятностей по возможным состоянии, т.е. . Неопределенность ситуации до определения сигнала характеризуется его энтропией объекта, измеряемой по формуле Шеннона: Н(А)=Н(Р₁,Р₂,…,Р_н)= .

После приема сигнала, если нет ошибок отсутствуют помехи, можно дать точный ответ в каком состоянии находится объект. Таким образом неопределенность наших знаний о состоянии объекта станет равной нулю, а с другой стороны полученное количество информации I равное разности энтропий объекта до и после сигнала. При отсутствии ошибок количество информации равно априорной энтропии: n – число символов послед-ти; m – объем алфавита. . Если в принимаемом сигнале есть ошибка, тогда об однозначности объекта говорить невозможно, т.е. энтропия не уменьшилась до 0. Для определения количества информации, в этом случае, необходимо учитывать и апостериорную энтропию.

Свойства энтропии: 1. Непрерывная, неотрицательная функция P_i: Н(Р₁,Р₂,…,Р_н)>=0. Если двоичная система: 0=<Н(Р₁,Р₂,…,Р_н)<=1.

2. Н(А)=0, если существует P_i=1

3. Н(А)→мах, т.е. Н(А)=1, если P_i равны друг другу.

4. Если состояние объекта образуется совместной реализацией состояний А_к, В_е, к=1,К; е=1,L. Н(АВ)=Н(А)+Н(В). Н(А)= ,

Н(В)=

18. Ортогональные разложения колебаний. Преобразование сообщений в ортогональные разложения колебаний. Ортонормированная система базисных функций. Большинство сложных сигналов, которые описывают сообщение, сигналы, помехи, состояния и т.д. целесообразно представлять в виде линейных комбинации, более простые сигналы с использованием системы заранее известных функций.

- такое разложение называют разложением x(t) по системе базисных функций φ_i(t). Требования к системе φ_i(t):

1) ортогональность: . При Q=1, систему называют ортонормированной.

, осуществляется по энергии и по мощности: По энергии:

По мощности:

2) условие теплоты:

Базис система является полной в том случае, если среднее квадратическая ошибка аппроксимации может быть доведена до малой величины ε, за счет увеличение членов ряда

. Для того чтобы представить сигнал х, необходимо получить коэффициент разложения a_i. Данная совокупность и есть спектральная характеристика сигнала в базисе . - обобщенный ряд Фурье.

Относительная величина ошибки: