7. Позиционные и непозиционные системы счисления. Алгоритм выполнения перевода и арифметических операций в разных системах счисления.

СИСТЕМА СЧИСЛЕНИЯ- способ изображения чисел и соответствующие ему правила действия над числами. Непозиционная СС- в которой от положения цифры в записи числа не зависит величина, которую она обозначает. Древнеегипетская десятичная непозиционная система счисления. Примерно в третьем тысячелетии до нашей эры древние египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел 1, 10, 100 и т.д. использовались специальные значки — иероглифы. Все остальные числа составлялись из этих ключевых при помощи операции сложения. Система счисления Древнего Египта является десятичной, но непозиционной.

В непозиционных системах счисления количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа. Например, чтобы изобразить 3252 рисовали три цветка лотоса (три тысячи), два свернутых пальмовых листа (две сотни), пять дуг (пять десятков) и два шеста (две единицы). Величина числа не зависела от того, в каком порядке располагались составляющие его знаки: их можно было записывать сверху вниз, справа налево или вперемежку.

Римская система записи чисел.

I	V	X	L	C	D	M
1	5	10	50	100	500	1000

CCXXXII=100+100+10+10+10+1+1=232 VI=6 IV=4

Цифры записываются слева направо в порядке убывания, если слева записана меньшая цифра, а справа большая, то их значения вычитаются.

Позиционные системы счисления Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов (цифр), необходимых для записи любых чисел.

Основанием позиционной системы счисления называется возводимое в степень целое число, которое равно количеству цифр, используемых для изображения чисел в данной системе счисления. Основание показывает также, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию. Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число не меньшее 2. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и тд.).

В позиционных системах счисления количественный эквивалент (значение) цифры зависит от ее места (позиции) в записи числа. Десятичная система характеризуется тем, что в ней 10 единиц какого-либо разряда образуют единицу следующего старшего разряда. Другими словами, единицы различных разрядов представляют собой различные степени числа 10. При обучении математике в школе используется десятичная система счисления. Она базируется на представлении чисел в системе с основанием 10 и незаменима при расчетах, которые нам приходится делать повседневно. Однако для компьютера более эффективной является система двоичных чисел. Эта система основана только на двух цифрах - 0 и 1 - и оказывается идеальной, поскольку во время работы компьютера используется электрический ток: он либо течет по цепи (цепь включена), либо не течет (цепь выключена). В компьютере двоичные числа 0 и 1 можно использовать для описания электрических сигналов по принципу включено-выключено. На этом простом принципе основана работа ЦП. Все входные данные преобразуются в нули и единицы, при этом нуль означает отсутствие тока в цепи, а единица - присутствие тока в цепи.

Два числа 0 и 1 называют битами. Слово "BIT" представляет собой сокращенную форму термина BInari digiT (двоичный разряд). Бит - это 0 или 1 и ничего более. Для представления любой буквы алфавита ПК использует байты. Комбинируя восемь нулей и единиц различными способами, можно представить 256 различных знаков. Например буква "L" в двоичной системе выражается кодом 01001100. Когда вы нажимаете клавишу с буквой L на клавиатуре, ЦП получает команды для восьми цепей: выключить-включить-выключить-выключить-включить-включить-выключить-выключить. Если учесть чрезвычайно высокое быстродействие компьютера, то станет очевидным, что для отображения на экране буквы практически не требуется никакого времени. Для восьми битов, составляющих байт, существует 256 возможных комбинаций, то есть более чем достаточно, чтобы представить все буквы алфавита. Комбинации, остающиеся неиспользованными для представления букв алфавита, используются для других целей. Каждое из десяти первых чисел десятичной системы имеет свою последовательность битов. Для каждого знака препинания и даже для пробела также требуется свой байт. Например число 7 выражается байтом 00110111; запятая - 00101100; пробел - 00100000.

Как перевести целое число из десятичной системы в любую другую позиционную систему счисления? При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

К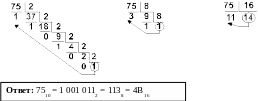 ак пеpевести пpавильную десятичную дpобь в любую другую позиционную систему счисления? Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть пpоизведения. Число в новой системе счисления записывается как последовательность полученных целых частей пpоизведения.

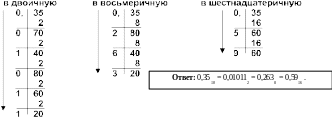
Умножение пpоизводится до тех поp, пока дpобная часть пpоизведения не станет pавной нулю. Это значит, что сделан точный пеpевод. В пpотивном случае пеpевод осуществляется до заданной точности. Достаточно того количества цифp в pезультате, котоpое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

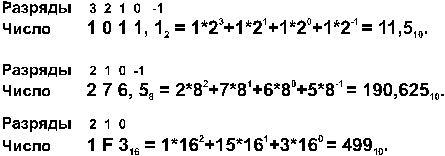Как пеpевести число из двоичной (восьмеpичной, шестнадцатеpичной) системы в десятичную? При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Примеpы:

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. П

Сложение в восьмеричной системе

ри сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

П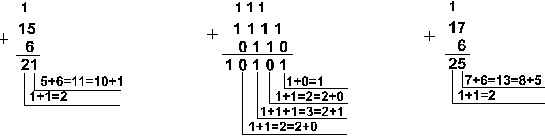 ример 1. Сложим числа 15 и 6 в различных системах счисления.

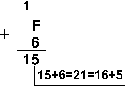Шестнадцатеричная: F₁₆+6₁₆

Вычитание

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.

Умножение

В 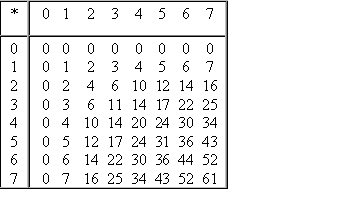ыполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения. Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям. Пример. Перемножим числа 115 и 51.

О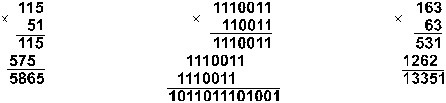 твет: 115*51 = 5865₁₀ = 1011011101001₂ = 13351₈.