§ 2. Определение эмпирических характеристик ряда прямых измерений

Из-за ограниченности числа результатов измерений при обра­ботке вместо математического ожидания и дисперсии получают их приближенные оценки — соответственно эмпирическое среднее и эмпирическую дисперсию S², характеризующие средний результат измерений и степень разброса результатов. Если число n результатов измерений небольшое (меньше 25), и S² определяют из выражений:

(II-7)

(II-8)

или

(II-9)

При большем числе результатов измерений, выраженных одно­значными или двузначными числами, их разбивают на равные ин­тервалы и производят подсчет частот т_i соответствующих каждо­му интервалу i.

Тогда

(II-10)

(II-11)

В выражениях (П-10) и (II-11) х_i — значение, соответствующее середине i-го интервала, а n — число интервалов, выбираемое в пределах от 10 до 15, в зависимости от зоны рассеивания результа­тов измерений и принятой величины интервала. Зона рассеивания равна разности между наибольшим и наименьшим результатами измерений. Величину интервала при измерении размеров удобно выбирать из ряда , , мм, где К — целое положи­тельное, отрицательное число или нуль.

Пример 1. При измерении величин радиальных биений наруж­ной поверхности втулок получено 200 результатов: от 0,01 до 0,25 мм. Величину зоны рассеивания — 0,24 мм предпочтительнее всего разбить на 12 интервалов по 0,02 мм. Последовательность обработ­ки показана в табл. II-1.

Решение. Вычисляем:

Номер интервала	Границы интервалов, мм		Середина интервала , мм	Частота
	свыше	до (вклю-чительно)
1	0,00	0,02	0,01	10	0,10	0,0010
2	0,02	0,04	0,03	35	1,05	0,0315
3	0,04	0,06	0,05	38	1,90	0,0950
4	0,06	0,08	0,07	33	2,31	0,1617
5	0,08	0,10	0,09	24	2,16	0,1944
6	0,10	0,12	0,11	25	2,75	0,3025
7	0,12	0,14	0,13	17	2,21	0,1873
8	0,14	0,16	0,15	5	0,75	0,1125
9	0,16	0,18	0,17	7	1,19	0,2023
10	0,18	0,20	0,19	3	0,57	0,1083
11	0,20	0,22	0,21	2	0,42	0,0882
12	0,22	0,24	0,23	1	0,23	0,0529
Сумма				200	15,64	1,5376

Эмпирическое среднее квадратическое отклонение

мм.

Если результаты измерений выражены трехзначными числами, и более, расчет целесообразно вести путем введения новой случайной величины :

(II-12)

где x_о — условное среднее (обычно принимается одно из значений x_i, лежащее в середине ряда); h — величина интервала.

Вычисляем начальные моменты первый а₁ и второй а₂.

(II-13)

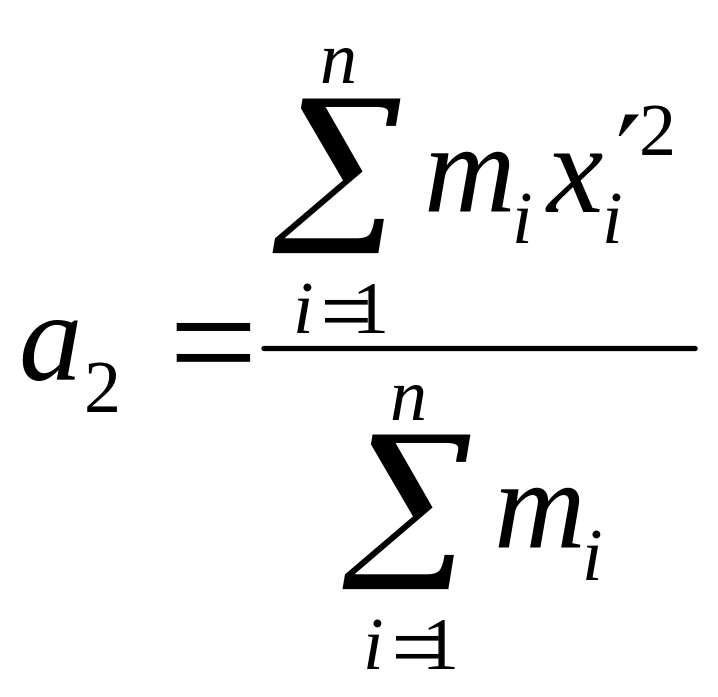(II-14)

После чего и определяем из выражений:

(II-15)

(II-16)

Пример 2. При измерении диаметра валиков для партии 360 шт. наибольший размер составляет 41,923 мм, а наименьший — 41,898 мм. Величину зоны рассеивания — 25 мкм предпочтительнее всего разбить на 13 интервалов по 2 мкм. Последовательность обработки показана в табл. II-2, где x_о принято равным 41,910 мм.

Таблица II-2

Номер интервала	Границы интервалов, мм		Середина интервала , мм	Частота
	Свыше	До (вклю-чительно)
1	41,897	41,899	41,898	1	-6	-6	35
2	41,899	41,901	41,900	3	-5	-15	75
3	41,901	41,903	41,902	6	-4	-24	96
4	41,903	41,905	41,904	27	-3	-81	243
5	41,905	41,907	41,906	35	-2	-70	140
6	41,907	41,909	41,908	48	-1	-48	48
7	41,909	41,911	41,910	68	0	0	0
8	41,911	41,913	41,912	68	1	68	68
9	41,913	41,915	41,914	33	2	66	132
10	41,915	41,917	41,916	36	3	108	324
11	41,917	41,919	41,918	27	4	108	432
12	41,919	41,921	41,920	5	5	25	125
13	41,921	41,923	41,922	3	6	18	108
Сумма				360		149	1827

Решение:

мм;

мм.