§ 8. Обработка результатов измерений по способу наименьших квадратов

Способ наименьших квадратов применяют при исследовании функциональной зависимости результата измерения пли погреш­ности у от некоторого фактора х. Размер детали может функцио­нально зависеть от температуры. Погрешности деталей в партии могут изменяться в функции времени из-за износа резца. В этих случаях требуется по экспериментальным данным наилучшим образом воспроизвести зависимость y = f(x).

Известно, что для n результатов измерений всегда можно подо­брать полином (n —1)-го порядка, удовлетворяющий всем полу­ченным парам значений , . Однако такой полином не будет отражать физической сущности функции f(x), поскольку каждое из значений случайно из-за воздействия целого ряда дополнитель­ных факторов (например, погрешности измерения). Поэтому возни­кает задача «сглаживания» экспериментально полученной зависи­мости, т. е. определение зависимости, не искаженной случайными выбросами значений .

Способ наименьших квадратов позволяет, предполагая из фи­зических оснований вид уравнения функциональной зависимости, определить такие конкретные параметры этого уравнения, чтобы сумма квадратов отклонений экспериментальных значений функ­ции от вычисленных согласно уравнению была бы наименьшей.

Если физический смысл явления предполагает наличие функцио­нальной зависимости в виде полинома m-й степени

,

коэффициенты а₀, а₁, а₂ и а_m определяем, как решения системы (m +1) уравнений:

(II-32)

где

.

Оценку среднего квадратического отклонения опытных дан­ных от данных, полученных по эмпирической формуле, определяем из выражения

(II-33)

Пример 14. По экспериментальным данным определить уравне­ние систематической погрешности y = f(x) электромеханического преобразователя малых перемещений х.

Решение. Исходя из принципа действия преобразователя, предполагаем наличие функциональной зависимости в виде поли­нома не выше второй степени, т. е. наличие одной из следующих за­висимостей:

или у=а₀,

или y = а₀+ а₁x,

или y = а₀+ а₁x+ а₂x².

Исходные данные и расчеты сведены в табл. П-7.

Полином нулевой степени. Систему уравнений сводим к одному:

;

;

.

Полином первой степени. Систему уравнений сводим к следующей:

;

;

Таблица II-7		0,0784	0,0256	0,0400	0,0484	0,0225	0,1764	0,0400	0,0900	0,0196	0,0081	0,5490
		0,28	0,16	0,20	0,22	0,15	0,42	0,20	0,30	0,14	0,09
		+0,58	-0,06	-0,2	-0,42	-0,45	-0,38	-0,30	-0,20	+0,26	+0,69
		+1,2	+2,5	0	-16,2	-60,0	-135,2	-98,0	+22,5	+129,6	+240,0	+86,4
		16	625	1296	6561	10000	28561	38416	50625	104976	160000	401076
		8	125	216	729	1000	2197	2774	3375	5832	8000	24226
		0,2025	0,0484	0,0121	0,0144	0,2809	0,5776	0,2209	0,0144	0,1521	0,3249	1,8482
		0,45	0,22	0,11	0,12	0,53	0,76	0,47	0,12	0,39	0,57
		-0,15	-0,12	-0,11	-0,08	-0,07	-0,04	-0,03	-0,02	-0,01	+0,03
		+0,6	+0,5	0	-1,8	-6,0	-10,4	-7,0	+1,5	+7,2	+12,0	-3,4
		4	25	36	81	100	169	196	225	324	400	1560
		0,1296	0,0256	0,0036	0,0196	0,2916	0,5476	0,1936	0,0256	0,2116	0,4356	1,8840
		0,36	0,16	0,06	0,14	0,54	0,74	0,44	0,16	0,46	0,66
		+0,3	+0,1	0	-0,2	-0,6	-0,8	-0,5	+0,1	+0,4	+0,6	-0,6
		2	5	6	9	10	13	14	15	18	20	112
		1	2	3	4	5	6	7	8	9	10	Сумма

Откуда

;

;

Полином второй степени. Систему уравнений сводим к следующей:

; ;

;

;

.

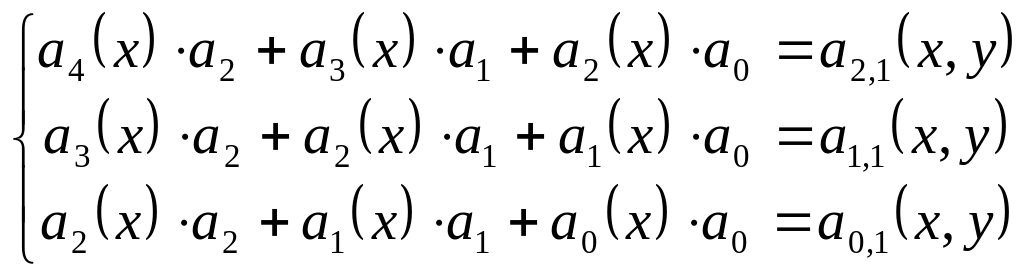
Сравнивая между собой , и , убеждаемся, что при приня­той гипотезе (погрешность описывается полиномом не выше второй степени) наилучшее приближение дает полином второй степени. Это показано на рис. II-4, где нанесены экспериментально получен­ные точки и кривые полиномов нулевой, первой и второй степени.