21.4. Принцип суперпозиции магнитных полей

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого в некоторой точке пространства системой токов, равна векторной сумме магнитных индукций, создаваемых в этой точке каждым из токов в отдельности.

. (21.4.1)

Применяя закон Био – Савара – Лапласа совместно с принципом суперпозиции, можно рассчитать магнитные поля токов различной формы.

21.5. Примеры вычисления магнитных полей

Считаем, что проводники с током находятся в вакууме .

1. Магнитное поле в центре кругового тока радиуса R.

В ыделим произвольный элемент проводника с током (рис. 21.5.1). Любой элемент, в каком месте витка он бы не находился, создает в центре витка магнитное поле одинакового направления – вдоль нормали (от витка). Поэтому сложение векторов можно заменить сложением их модулей. Все элементы проводника перпендикулярны радиусу-вектору , расстояние всех элементов проводника до центра кругового тока одинаково и равно . Поэтому . Тогда

. (21.5.1)

2. М агнитное поле на оси кругового тока радиуса R.

Для любого элемента тока , (рис. 21.5.2). Следовательно, в точке А элемент создает магнитное поле с индукцией . Разные элементы создают в точке А магнитные поля разных направлений, поэтому возможно только суммирование проекций различных векторов на координатные оси. В силу симметрии, при суммировании составляющие вектора , перпендикулярные оси Ох дадут нуль, следовательно,

достаточно учесть проекцию вектора на ось Ох: . Учитывая, что (из треугольника СОА) , получаем

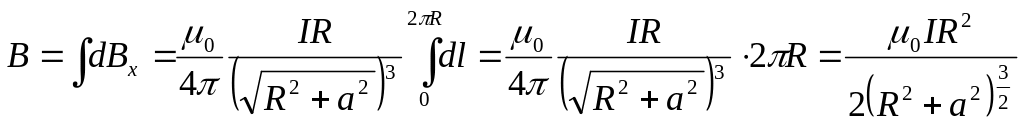. (21.5.2)

Если точка А находится далеко от контура , то величиной R можно пренебречь по сравнению с а. Тогда получим

,

где магнитный момент контура . При и произвольном расположении точки относительно центра контура, формула для расчета магнитного поля кругового тока в точке, задаваемой радиусом-вектором , имеет вид:

, (21.5.3)

где угол между радиусом-вектором и магнитным моментом кругового витка с током .

3. Магнитное поле прямого тока.

Рассмотрим ток, текущий по тонкому прямому проводнику (рис. 21.5.3). Произвольно выберем элемент тока . Индукция магнитного поля, создаваемого этим элементом в некоторой точке А, удаленной от оси проводника на расстояние , равна . На каком бы участке прямолинейного проводника мы не выбрали элемент с током, направление вектора будет одним и тем же (из плоскости чертежа на нас). Поэтому сложение векторов можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол угол между векторами и , выразив через него все остальные величины. Рассмотрим приращение , соответствующий элементу .

Из треугольника АЕD находим (т.к. угол мал). Из треугольника САО: , из треугольника СЕD: . Следовательно, магнитная индукция, создаваемая элементом проводника, равна

.

Проведем интегрирование

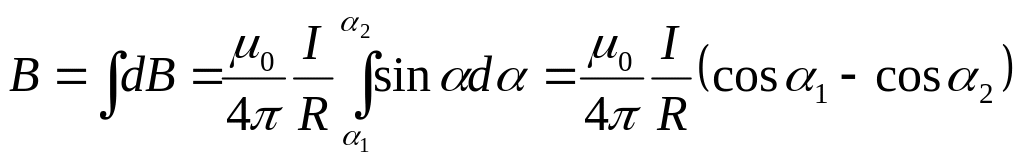. (21.5.4)

Если проводник с током имеет бесконечную длину, то угол для всех эле-

ментов изменяется в пределах от до , и, следовательно, магнитная индукция бесконечного прямого проводника с током

. (21.5.5)

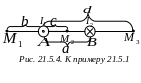
П ример 21.5.1. По двум прямолинейным параллельным бесконечно длинным проводникам, находящимся на расстоянии , текут токи и противоположного направления (рис. 21.5.4). Найти напряженность магнитного поля, созданного этими токами, в точках . Расстояния от проводников до точек равны: , , . Точки лежат на прямой, соединяющей проводники.