§10.4 Многоемкостные объекты без самовыравнивания.

Такие объекты, как и одноемкостные, после приложения к ним возмущения не приходят самостоятельно к состоянию равновесия. Свойства подобных объектовт рассмотрим на примере двухемкостного объекта (рис.10.5).

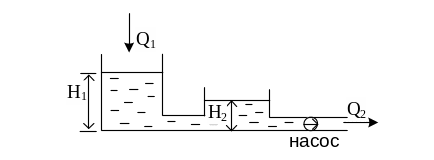
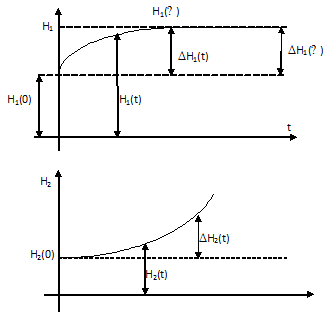
Регулируемая величина является отклонением уровня воды во 2-м бассейне , а возмущающим воздействием – изменение притока .

Такой объект можно представить в виде последовательного соединения апериодического звена 1-го порядка (1-й бассейн) с передаточной функцией:

и идеального интегрирующего звена (2-й бассейн) с передаточной функцией:

где - приращение притока во 2-й бассейн.

Передаточная функция объекта:

Таким образом, указанный объект в динамическом отношении подобен реальному интегрирующему звену.

Регулируемая величина не стремится к новому установившемуся значению.

§10.5 Объекты регулирования с запаздыванием.

Все перечисленные объекты регулирования могут иметь транспортное запаздывание, при котором изменение регулируемой величины начинается спустя некоторое время t после нанесения возмущения. В этом случае передаточная функция, полученная ранее, умножается на величину :

и т.д.

Переходные характеристики одноемкостных объектов с запаздыванием.

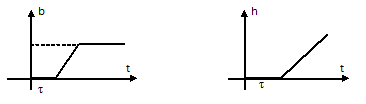
§11. Законы регулирования и регуляторы.

Будем считать, что на вход регулятора подается сигнал ошибки (рассогласование) между заданным и действительным значениями регулируемой величины (рис11.1) е(t)=g(t)-y(t)

Рис. 11.1

Определение: Функциональная связь между выходной величиной регулятора(регулирующим воздействием) u(t) и его входной величиной e(t) называется законом регулирования.

На практике используют следующие типовые законы регулирования:

1. Пропорциональный закон(П-закон)

В этом случае регулирующее воздействие вырабатывается лишь в зависимости от величины и знака рассогласования. u(t)=F[e(t)]

2. Интегральный закон (И-закон)

u(t)=

3. Пропорционально-интегральный закон (ПИ-закон)

u(t)=F[e(t); ]

4. Пропорционально-дифференциальный закон (ПД-закон)

u(t)=F[e(t), e’(t)]

5. Пропорционально-интергрально-дифференциальный (ПИД закон)

u(t)=F[e(t), , e’(t)]

§ 11.1 Пропорциональный регулятор.

Регулятор, регулирующий П-закон регулирования называется пропорциональным (П-регулятор).

У идеального П-регулятора выходная величина в пределах зоны регулирования изменяется пропорционально изменению входной величины. Уравнение динамики идеального П-регулятора имеет вид: u(t)=

- коэффициент передачи регулятора. =

В динамическом отношении идеальный П-регулятор представляет пропорциональное(усилительное) звено с передаточной функцией =

Рассмотрим особенности процесса регулирования при П-законе. В качестве объекта выберем одноемкостный объект с самовыравниваем рассм. ранее.

Рис. 11.1

Когда в бассейне произойдет отклонение уровня, регулятор тотчас не уменьшит на пропорциональную величину проходное отверстие регулирующего клапана К1.

Приток жидкости уменьшится, поэтому уровень будет расти с меньшей скоростью. Дальнейшее закрытие клапана и соответствующее уменьшение Q1 происходит по мере увеличения уровня жидкости. Баланс потоков жидкости достигается за счет совместного самовыравнивания (рост Q2) и уменьшения регулятором потока текущей жидкости Q1. Процесс регулирования закончится, когда установится равенство (рис 11.2)

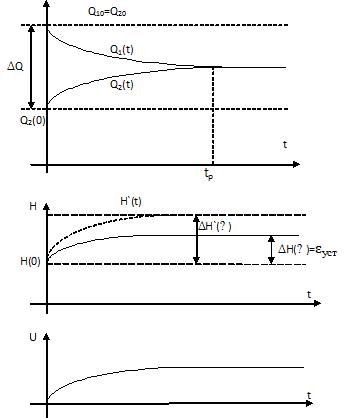
Рис. 11.2

Однако регулируемая величина не вернется к заданному уровню – в системе будет постоянное по величине отклонение , которое в общем случае называется установившейся (сшсмичесок) ошибкой .

Положительным фактором П-регулятора является его сшродействие. Из рисунка 11.2 следует что использование П-регулятора привело к уменьшению остаточного отклонения по сравнению со случаем отсутсвия регулятора ( < .