5.2 Примеры

Пример. Является ли сильно связным орграф, матрица смежности которого имеет вид:

?

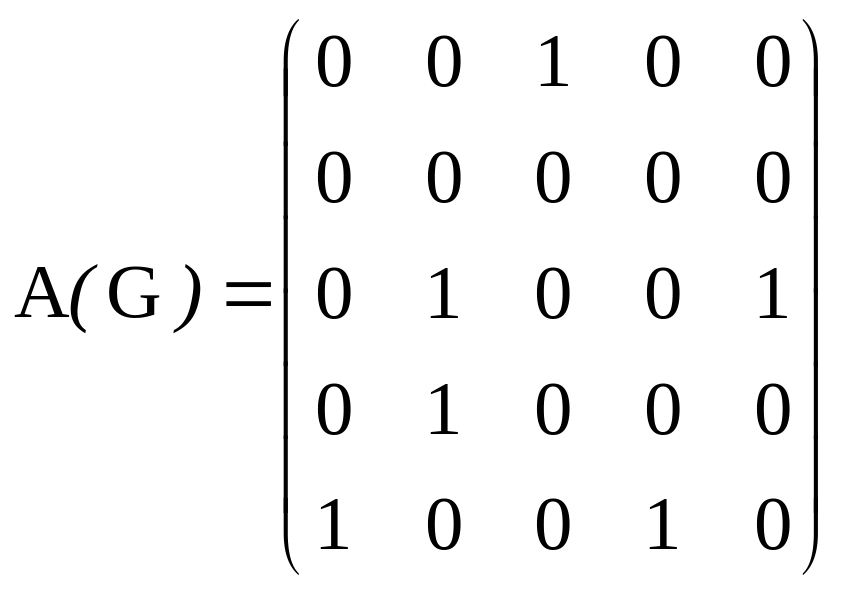Если нет, то найти компоненты сильной связности.

Решение

Сначала определим матрицу сильной связности данного графа:

.

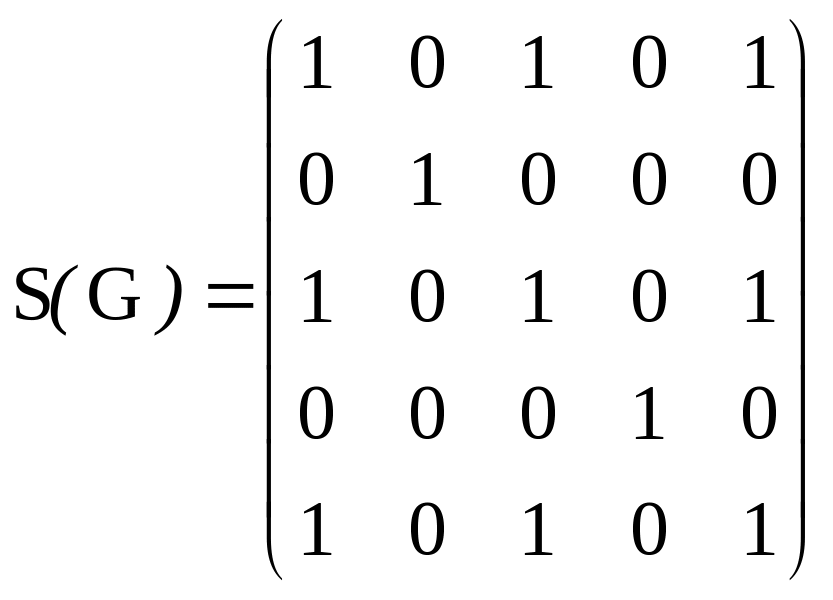Матрица сильной связности S(G) содержит нули, следовательно, орграф не является сильно связным. Образуем первую компоненту сильной связности. Это орграф, вершины которого соответствуют единицам первой строки матрицы сильной связности. Множество вершин G₁ - первой компоненты сильной связности: . В качестве матрицы смежности G₁ берем подматрицу матрицы А(G), находящуюся на пересечении первой, третьей, пятой строк с первым, третьим, пятым столбцом:

.

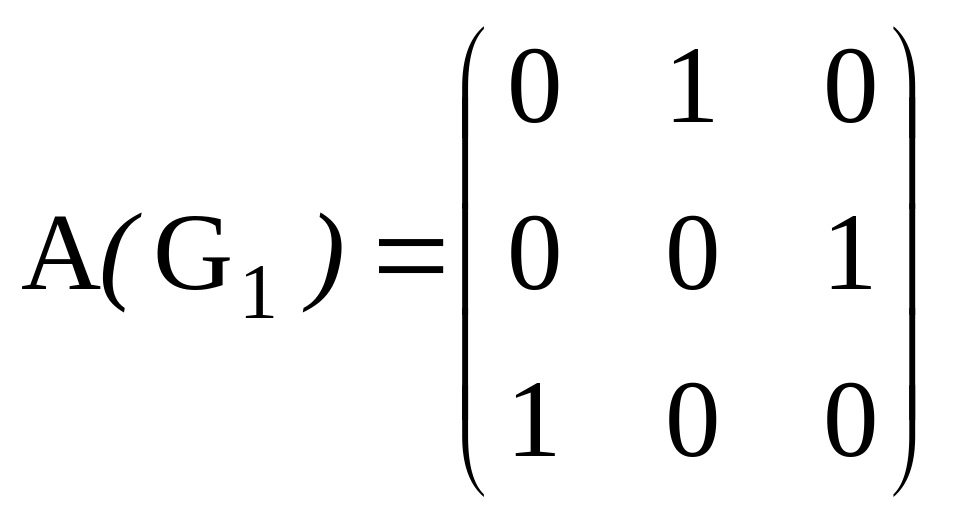Вычеркиваем из матрицы первую, третью, пятую строки, а также первый, третий, пятый столбцы, переходим к матрице . С помощью нее определяем множество вершин G₂ - второй компоненты сильной связности: . Матрица смежности G₂ имеет вид: .

Вычеркивая из матрицы S₂ первые строку и столбец, получаем матрицу . Третья компонента сильной связности G₃ содержит одну вершину – х₄ и характеризуется матрицей смежности .

В результате вычеркивания первых строки и столбца из матрицы S₃ ничего не осталось. Работа алгоритма прекращена. Орграф имеет три компоненты сильной связности.

3. Варианты задачи №9

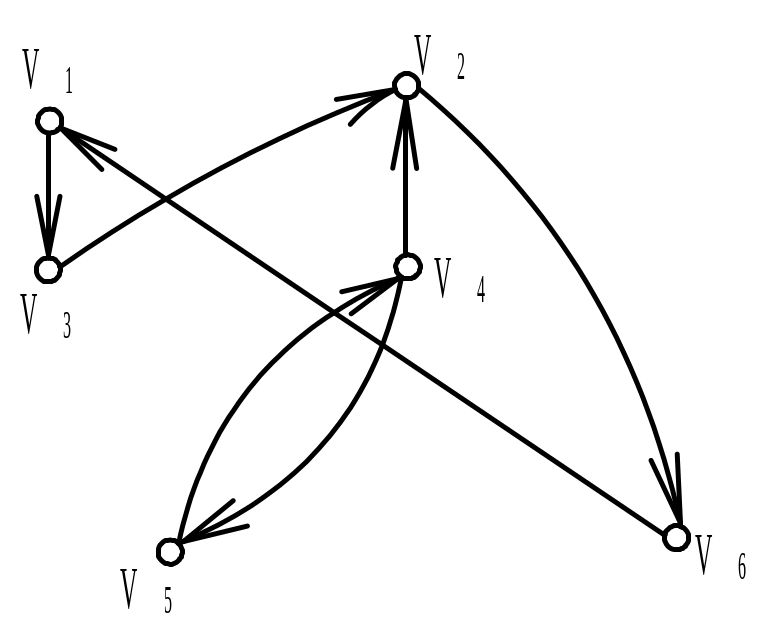
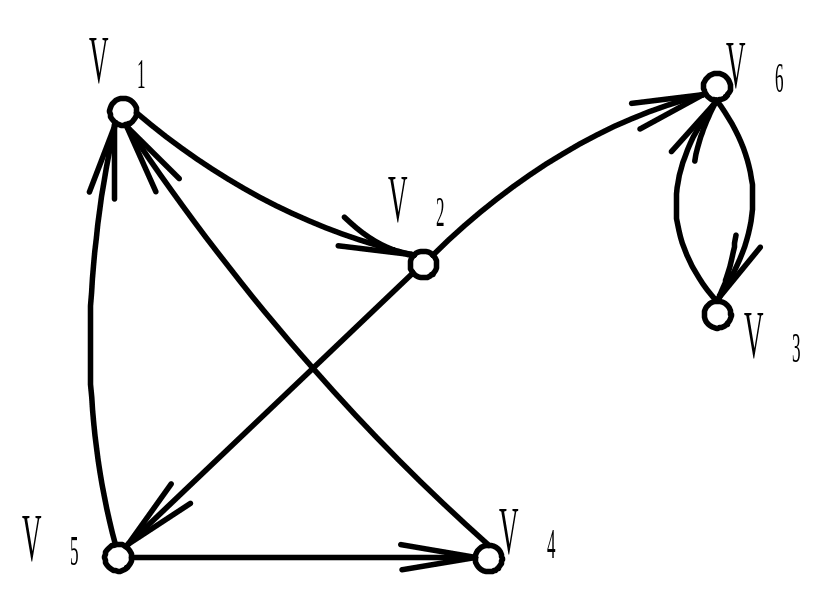
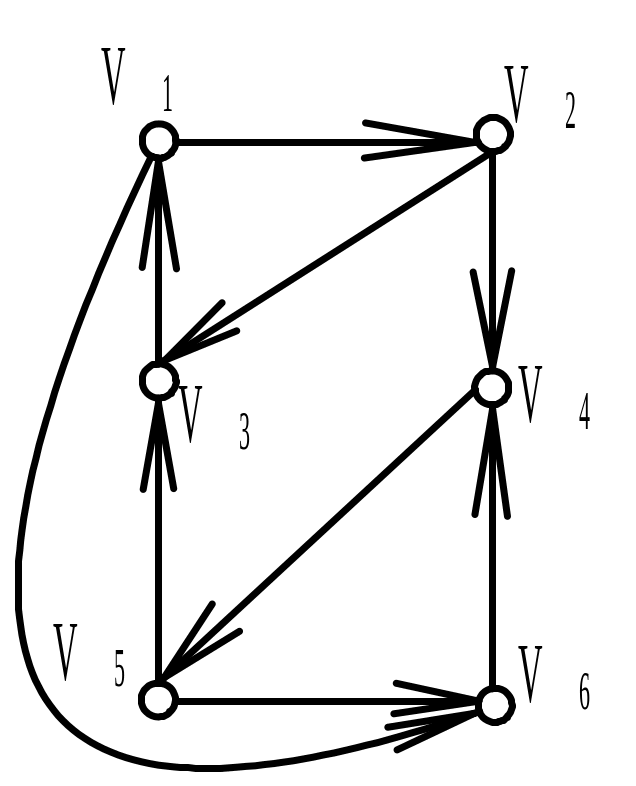
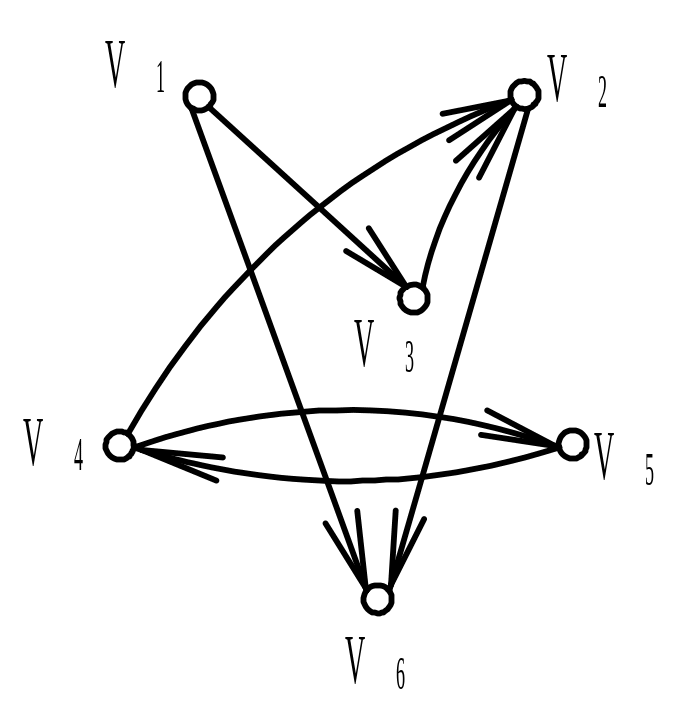
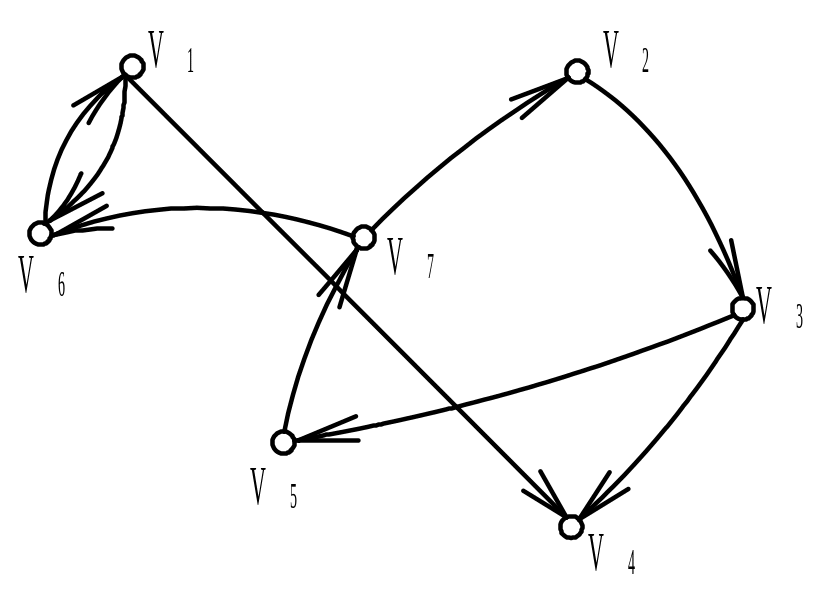
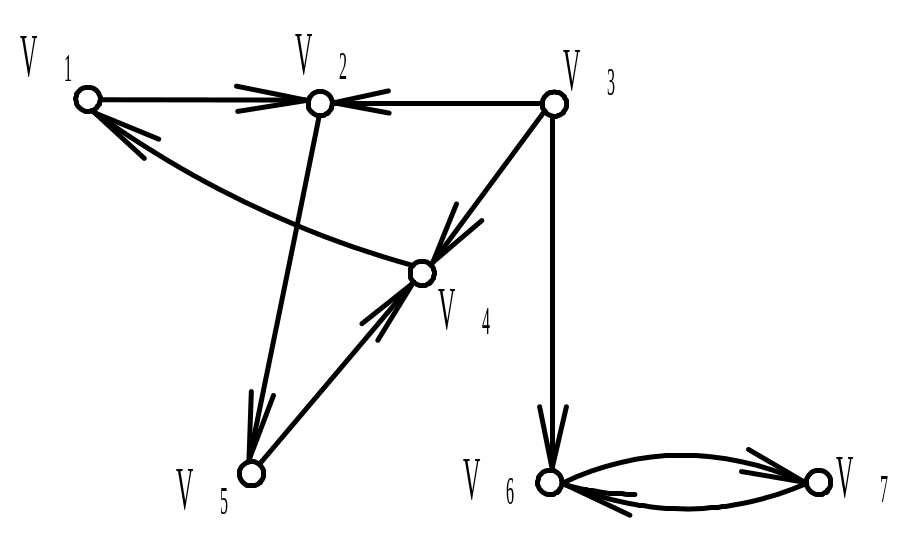
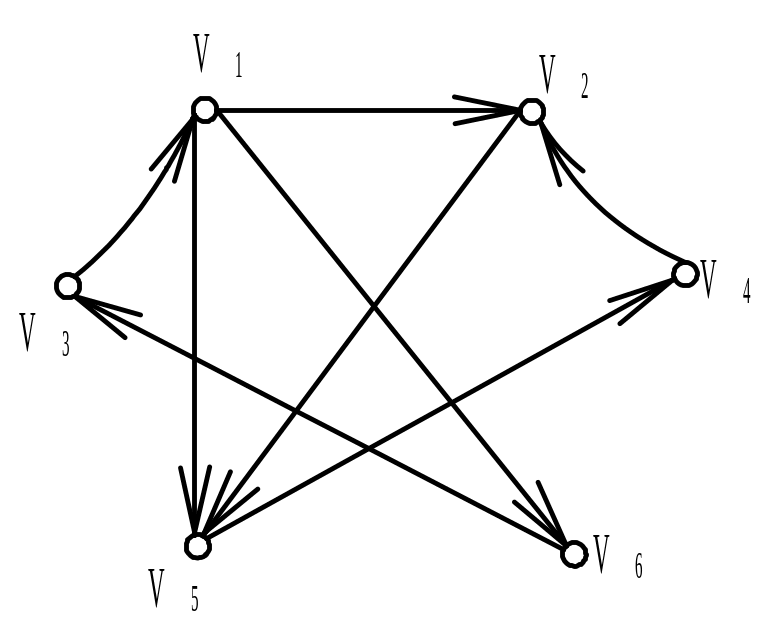
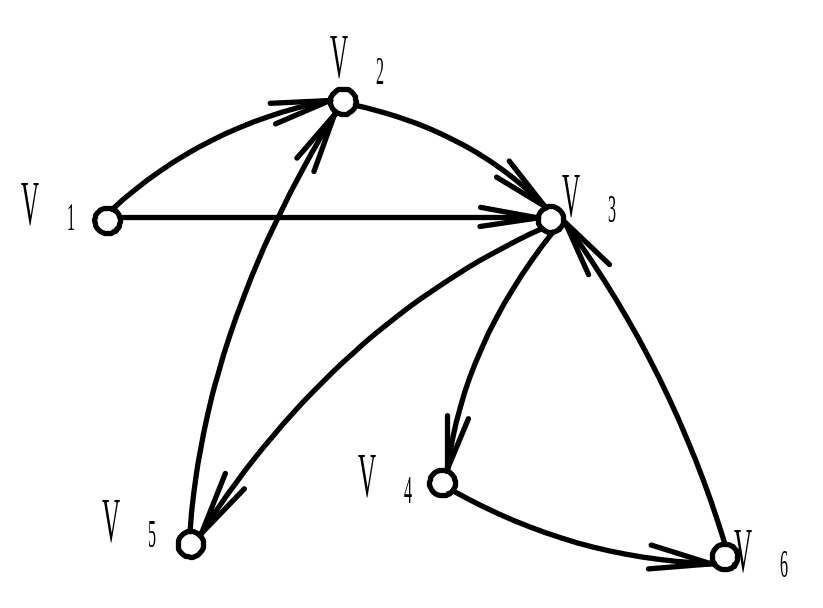
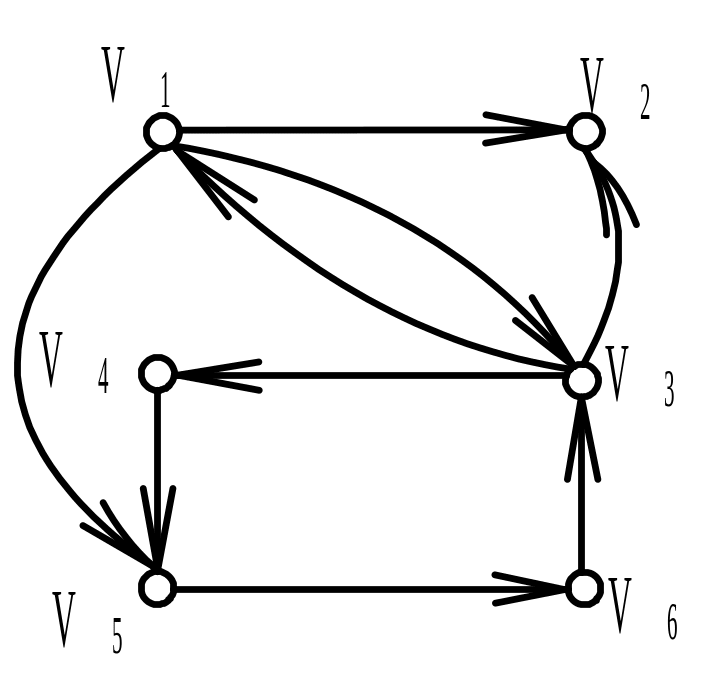
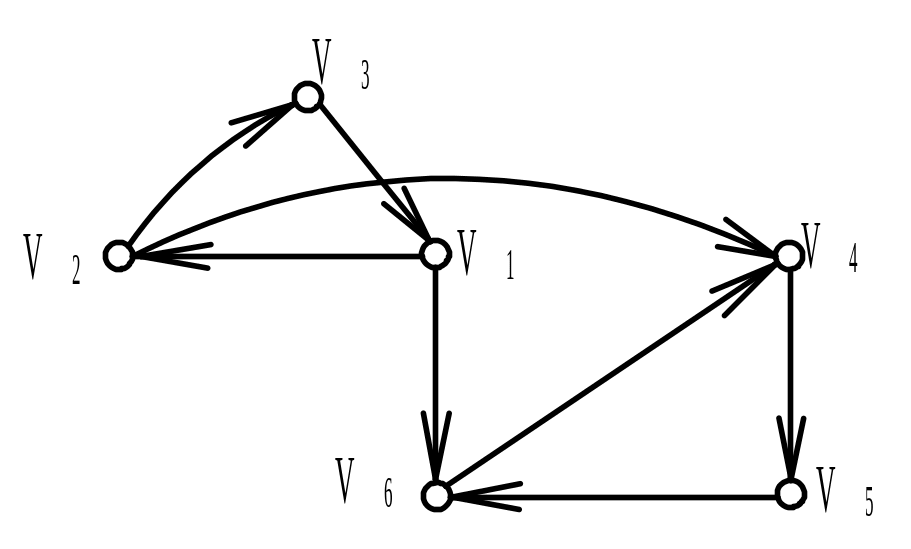
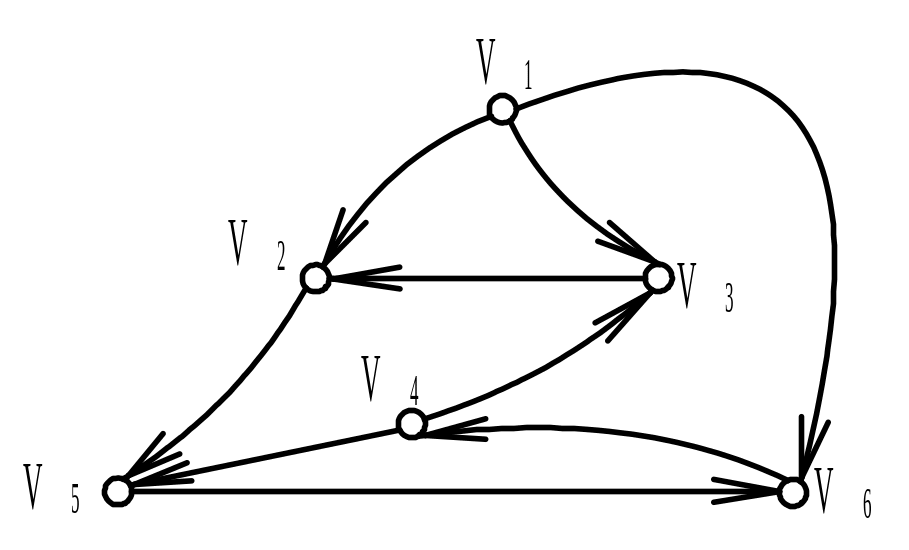
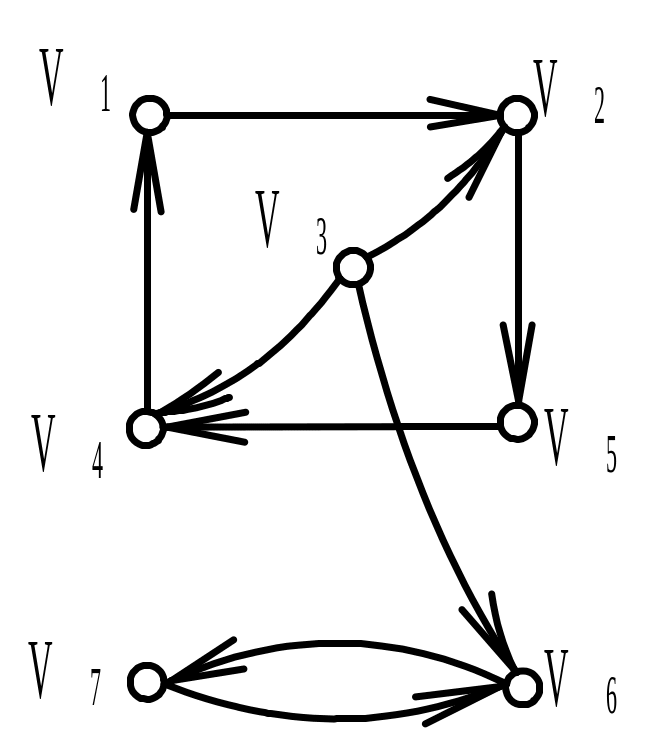
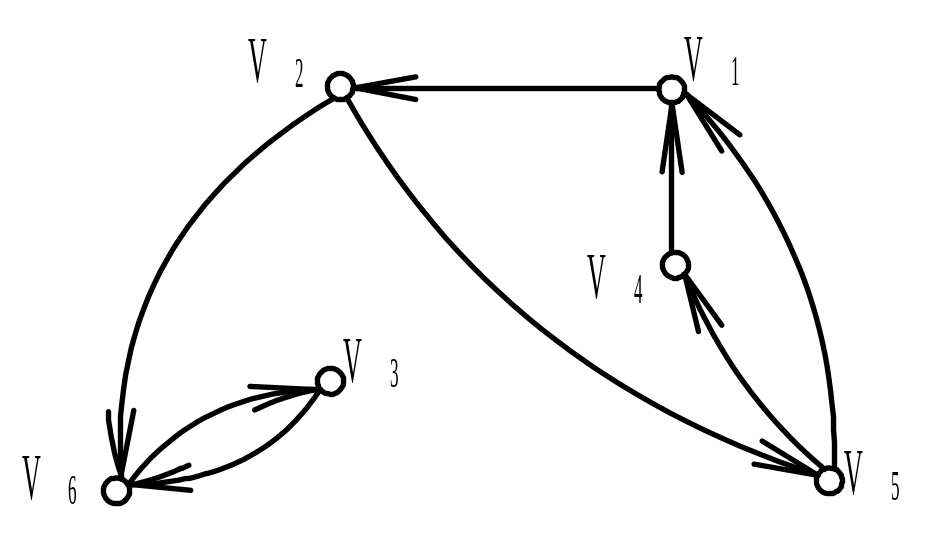
Найти матрицу смежности А ориентированного графа G (диаграмма дана на рисунке). Обозначить дуги и найти матрицу инцидентности В орграфа. Найти матрицу сильной связности S. Выделить компоненты сильной связности орграфа G. Построить диаграммы компонент сильной связности.

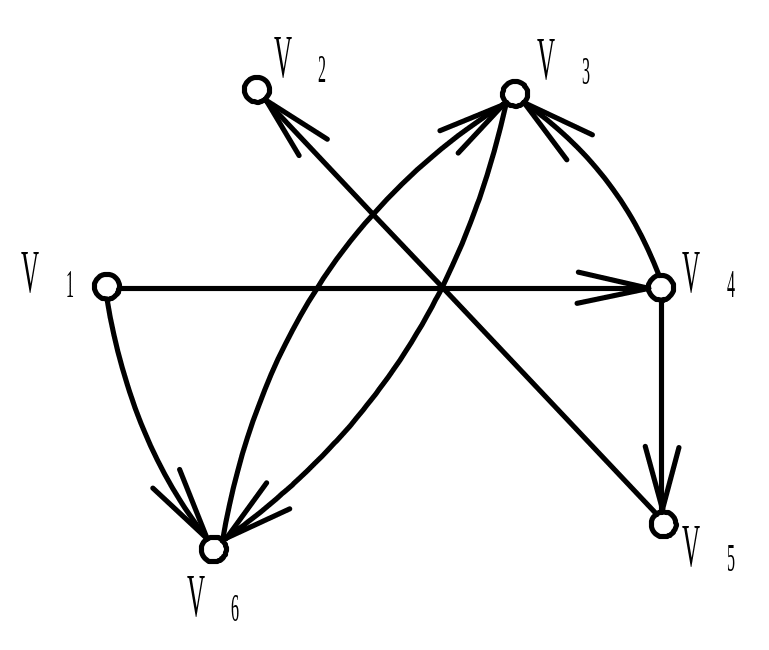
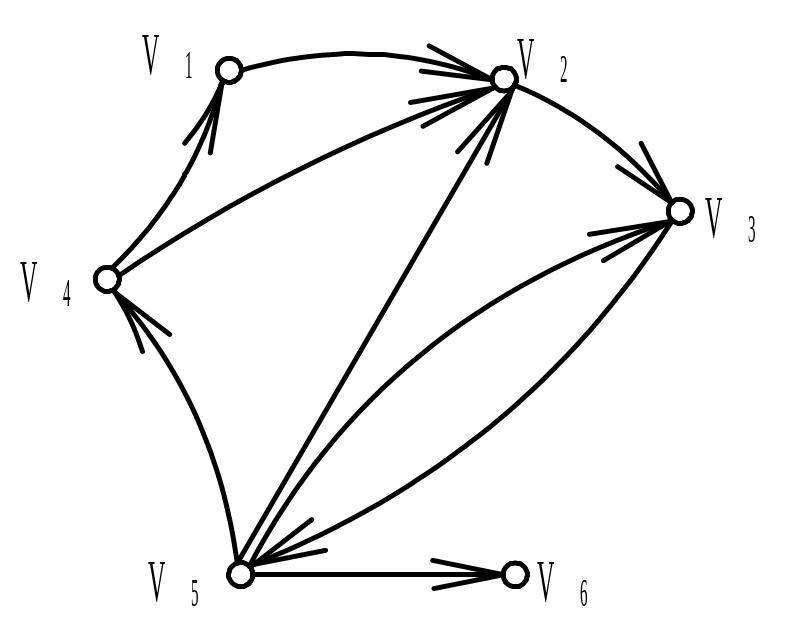
Вариант 1	Вариант 2	Вариант 3
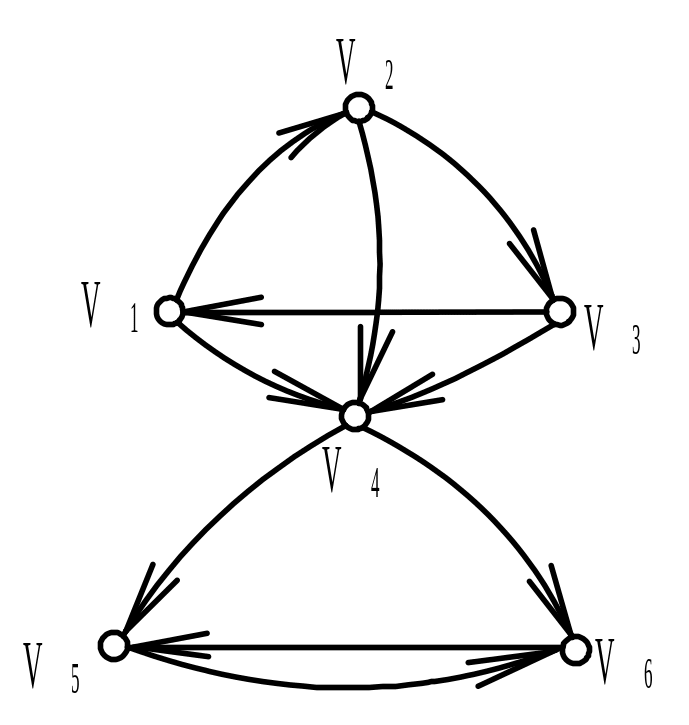
Вариант 4	Вариант 5	Вариант 6
Вариант 7	Вариант 8	Вариант 9
Вариант 10	Вариант 11	Вариант 12
Вариант 13	Вариант 14	Вариант 15
Вариант 16	Вариант 17	Вариант 18
Вариант 19	Вариант 20	Вариант 21
Вариант 22	Вариант 23	Вариант 24
Вариант 25	Вариант 26	Вариант 27
Вариант 28	Вариант 29	Вариант 30

5.4 Нахождение кратчайших путей

Орграф G(X, A) называется взвешенным, если каждой дуге (x,y) поставлено в соответствие некоторое действительное число l(x, y) - вес дуги (x, y). Весом маршрута x₁,x₂, …,x_n, x_n+1 называется число l= . Взвешенным расстоянием (w- расстоянием) между вершинами x и y называется минимальный из весов (x, y) – маршрутов. (x, y) – маршрут, вес которого равен расстоянию , называется кратчайшим (x, y) – маршрутом во взвешенном графе G.

Алгоритм Форда-Беллмана позволяет определить кратчайшее расстояние от фиксированной вершины графа G, называемой источником, до всех других вершин этого графа.

Задаётся строка D⁽¹⁾=(d₁⁽¹⁾, d₂⁽¹⁾, ..., d_n⁽¹⁾), полагая d_i⁽¹⁾=0, d_j⁽¹⁾=w_ij, i≠j. В этой строке d_j⁽¹⁾ (i≠j) есть вес w_ij дуги (x_i, x_j), если (x_i, x_j) существует, и d_j⁽¹⁾=∞, если дуга (x_i, x_j) отсутствует в G. Далее определяется строка D⁽²⁾=(d₁⁽²⁾, d₂⁽²⁾, ..., d_n⁽²⁾), полагая d_j⁽²⁾=min{ d_j⁽¹⁾, d_k⁽¹⁾ + w_kj}_{k=1, ..., n}. При этом d_j⁽²⁾ - минимальный из весов (x_i, x_j) – маршрутов, состоящих не более, чем из двух дуг.

Продолжая процесс, на шаге s определяется строка D^(s)=(d₁^(s), d₂^(s), ..., d_n^(s)), полагая d_j^(s)=min{ d_j^(s-1), d_k^(s-1) + w_kj}_{k=1, ..., n}. Искомая строка w-расстояний получается при s=n – 1: d_j^(n-1) = . Работа алгоритма завершается на шаге k, если D^(k) = D^(k+1).

Задача. Найти кратчайшие расстояния от вершины 1 до всех других вершин в орграфе G с матрицей весов W:

.

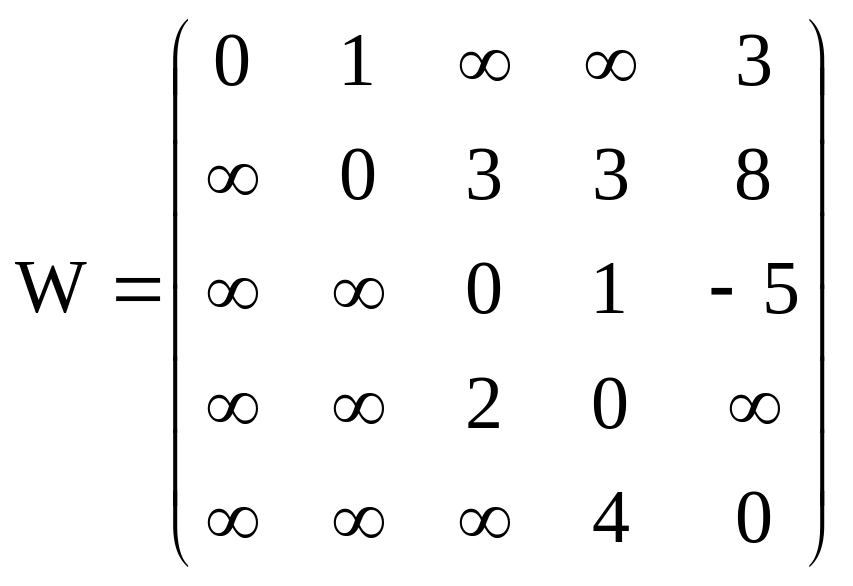Решение

Выберем в качестве источника вершину 1. Тогда D⁽¹⁾=(0, 1, ∞, ∞, 3), D⁽²⁾=(0, 1, 4, 4, 3), D⁽³⁾=(0, 1, 4, 4, -1), D⁽⁴⁾=(0, 1, 4, 3, -1). Таким образом, , , , , .