- •Дискретная математика
- •Введение
- •1 Теоретические вопросы
- •1 Основы теории множеств
- •1.1 Основные понятия и операции
- •1.2 Примеры
- •1.3 Варианты задачи №1
- •1.4 Варианты задачи №2
- •2 Отношения
- •2.1 Основные понятия и формулы
- •2.2 Примеры
- •2.3 Варианты задачи №3
- •3 Основы комбинаторики
- •3.1 Основные формулы
- •Примеры
- •3.3 Варианты задачи №4
- •3.4 Варианты задачи №5
- •Элементы математической логики
- •4.1 Основные понятия и формулы
- •Примеры
- •4.3 Варианты задачи №6
- •4.4 Варианты задачи №7
- •4.5 Варианты задачи №8
- •Основы теории графов
- •Основные понятия и формулы
- •5.2 Примеры
- •Варианты задачи №9
- •5.4 Нахождение кратчайших путей
- •5.5 Варианты задачи №10
- •Сетевое планирование
- •Основные понятия и формулы
- •Примеры
- •Варианты задачи №11
- •Содержание
3.4 Варианты задачи №5
Решить уравнения 1 – 13:
 .
.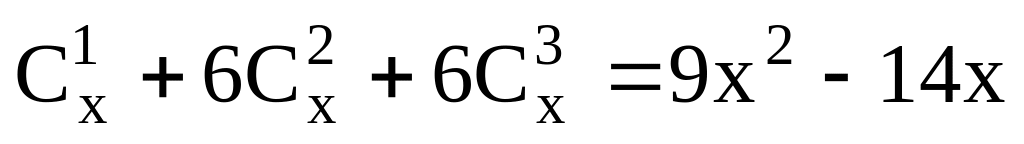 .
. .
.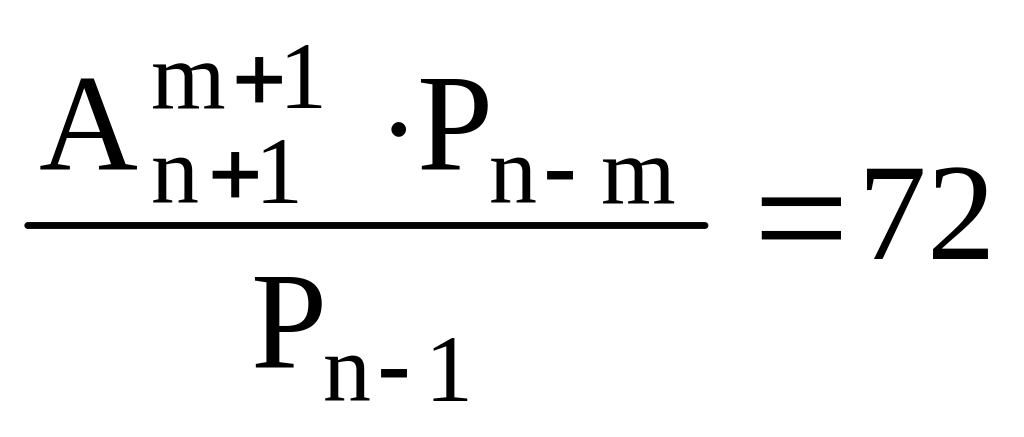 .
.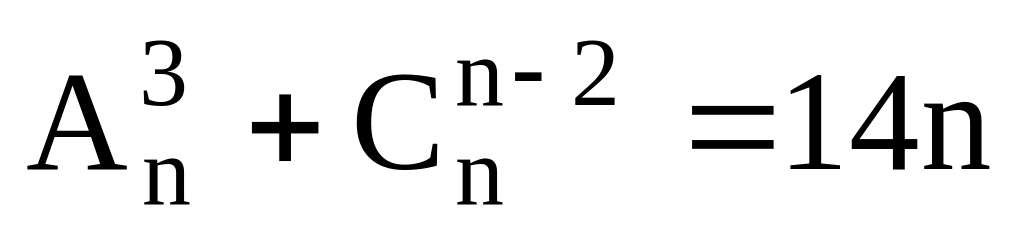 .
.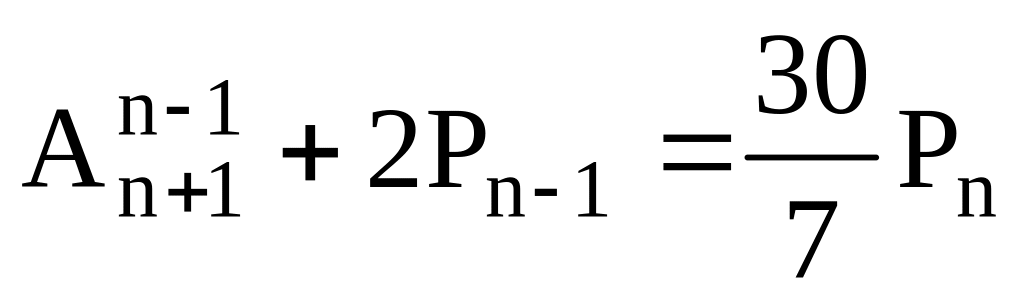 .
.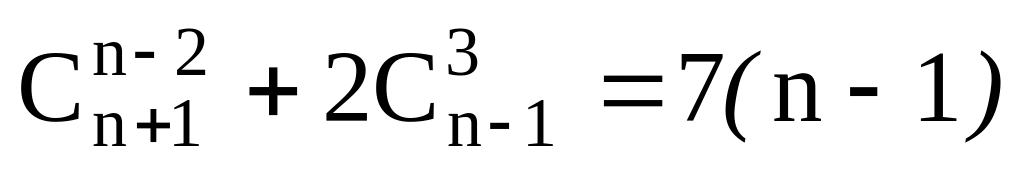 .
.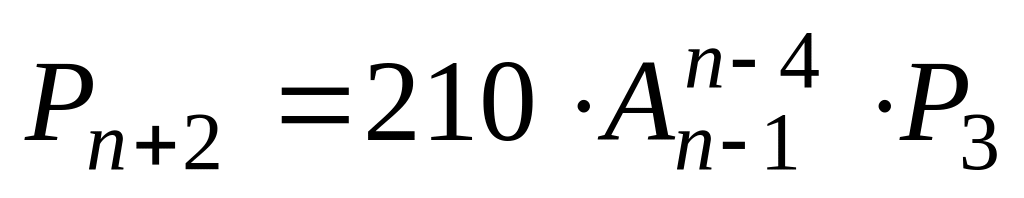 .
.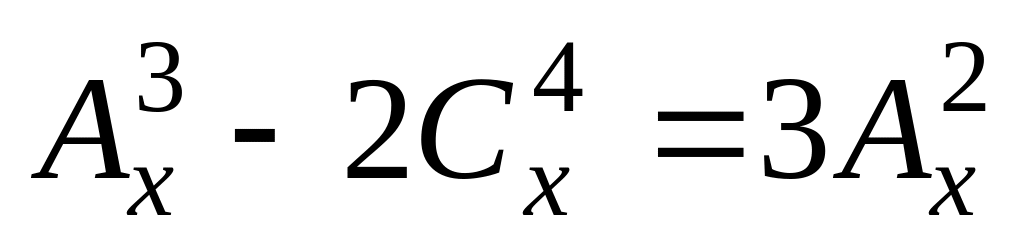 .
.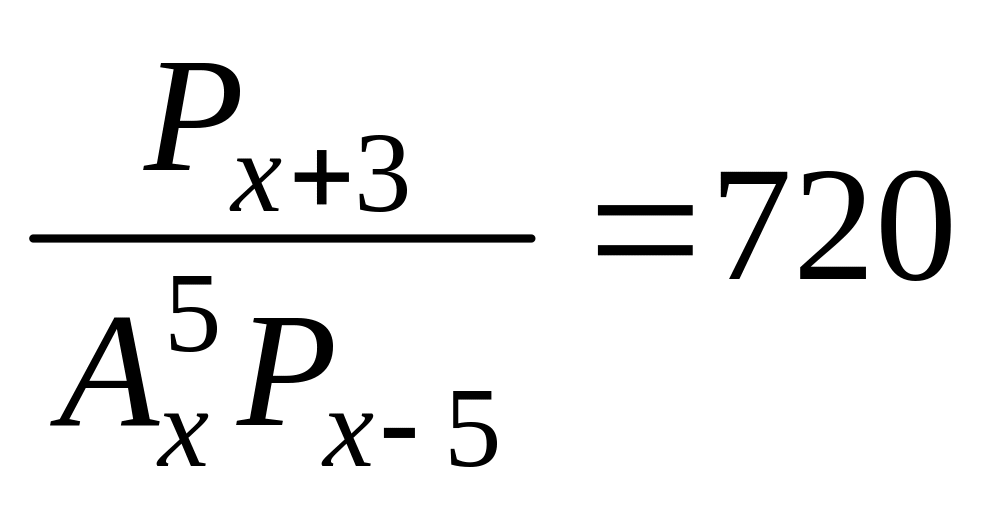 .
. .
.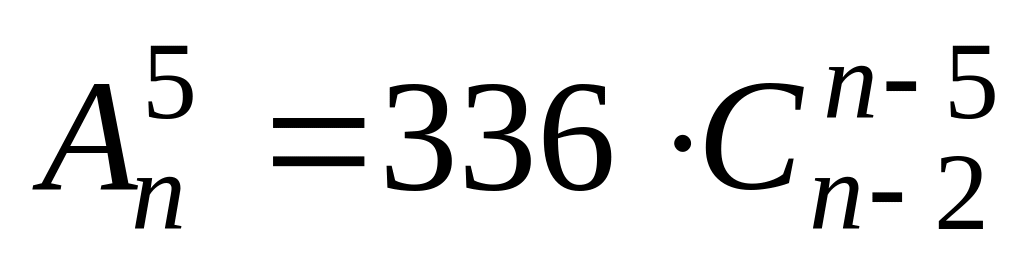 .
.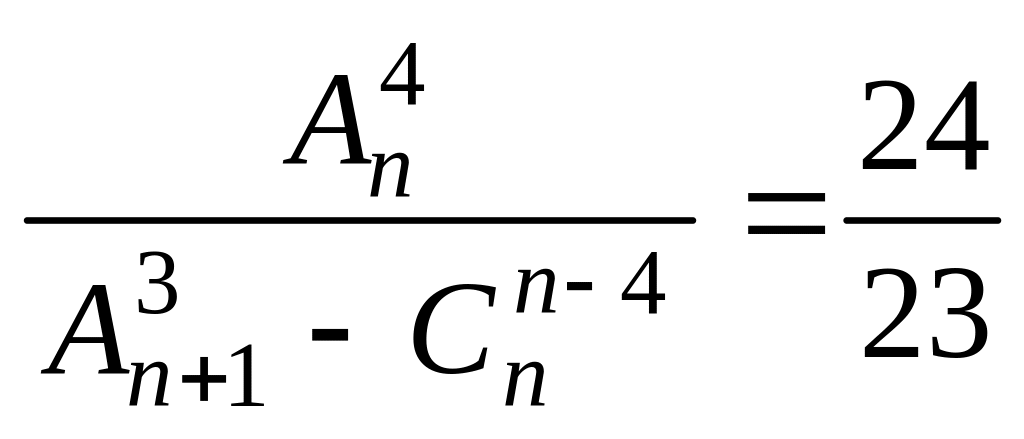 .
.Показать, что при любом k сумма
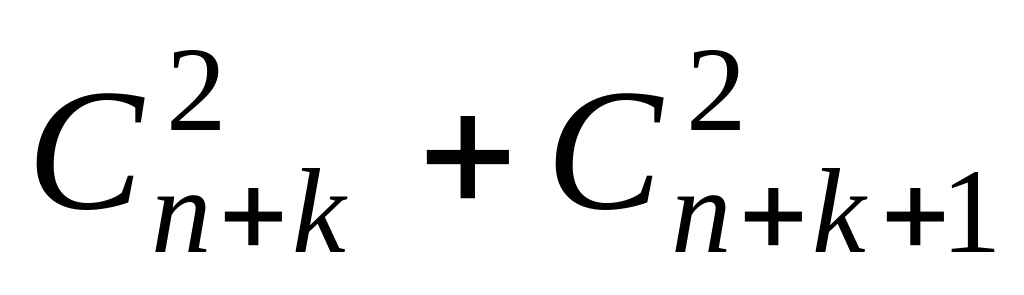 есть точный квадрат.
есть точный квадрат.Доказать тождество
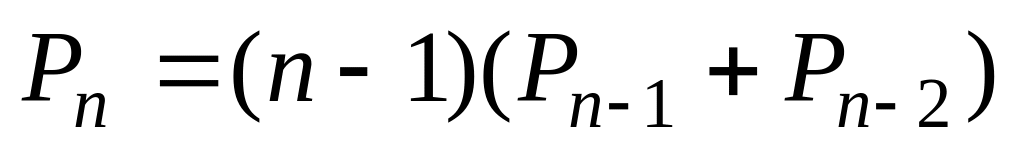 .
.Доказать тождество
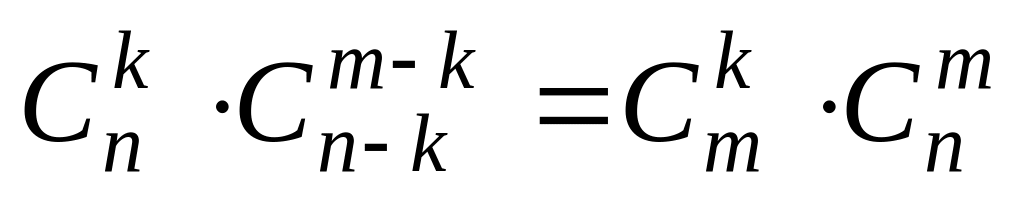 .
.Сумма биномиальных коэффициентов равна 256. Найти коэффициент члена бинома Ньютона
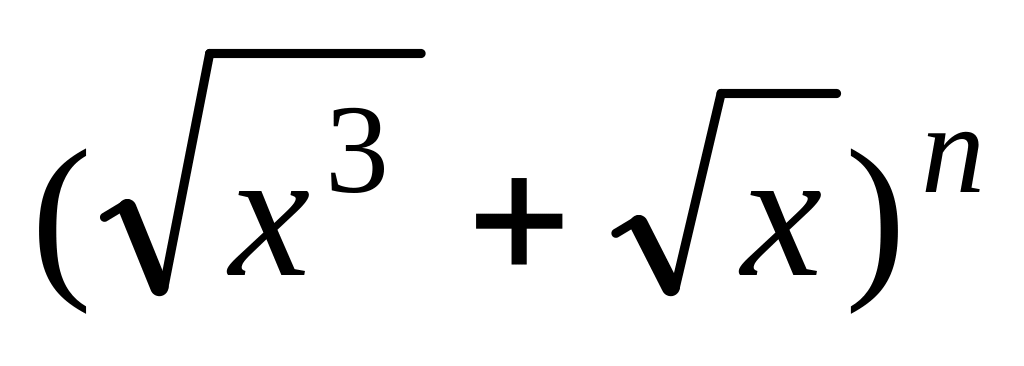 ,
который содержит
,
который содержит
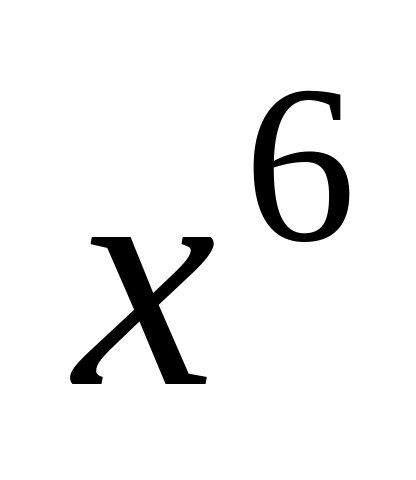 .
.Каков наибольший коэффициент разложения
 ,
если сумма всех коэффициентов равна
4096?
,
если сумма всех коэффициентов равна
4096?Сумма биномиальных коэффициентов разложения
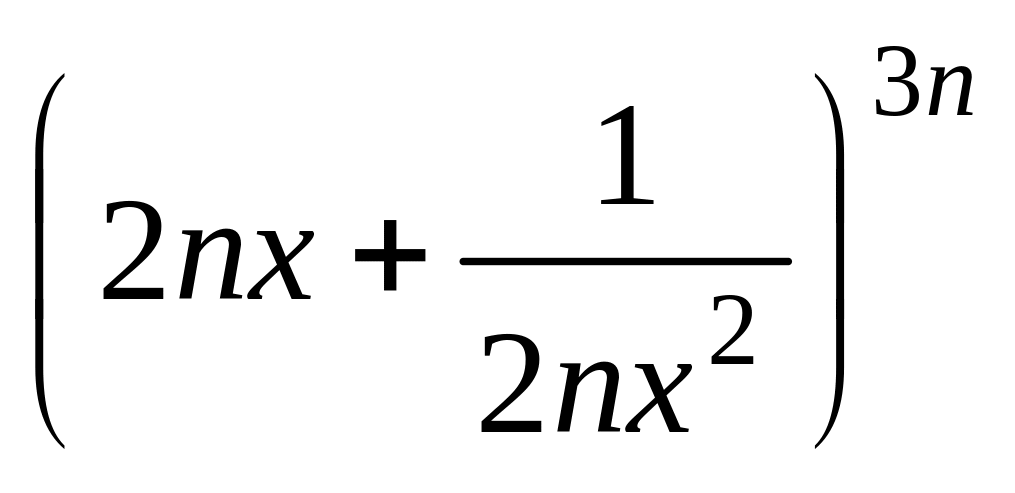 равна 64. Найти слагаемое, не содержащее
x.
равна 64. Найти слагаемое, не содержащее
x.Сумма биномиальных коэффициентов с нечетными номерами в разложении
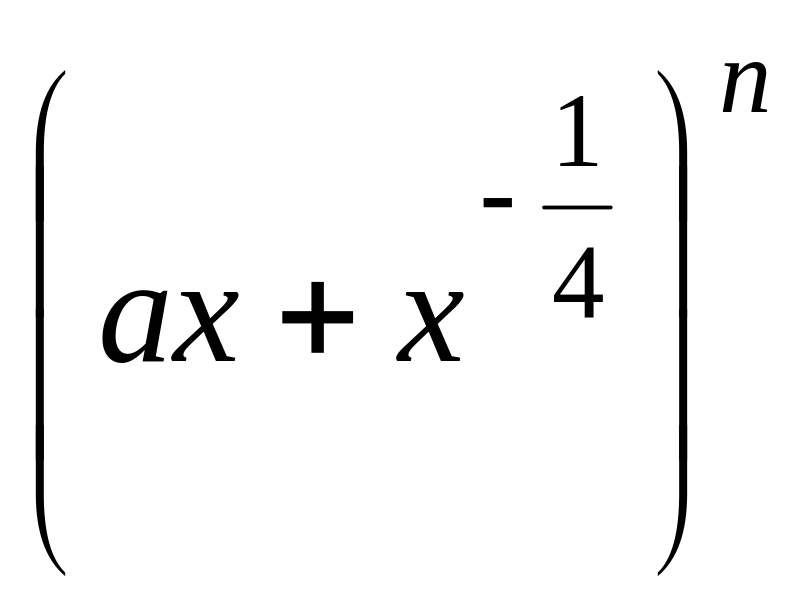 равна 512. Найти слагаемое, не содержащее
x.
равна 512. Найти слагаемое, не содержащее
x.Определить
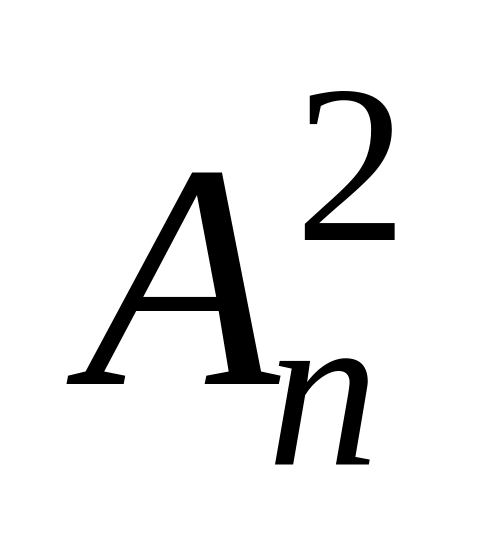 ,
если пятое слагаемое разложения
,
если пятое слагаемое разложения
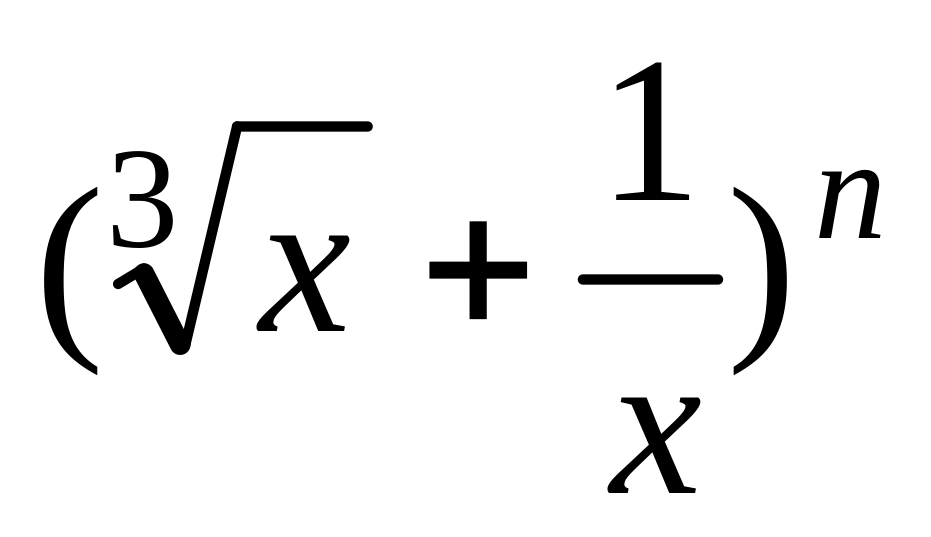 не зависит от x.
не зависит от x.В разложении
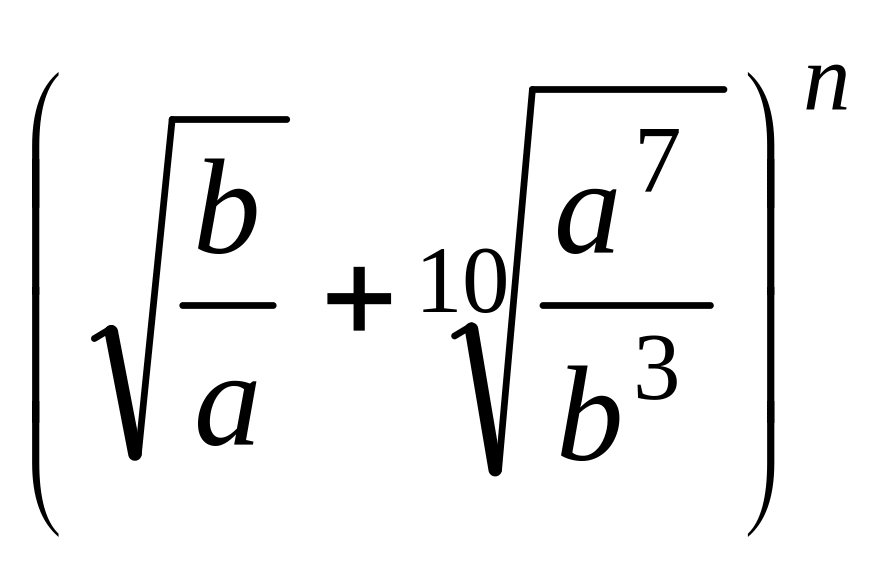 имеется член, содержащий ab.
Найти этот член.
имеется член, содержащий ab.
Найти этот член.В какую натуральную степень следует возвести бином
 ,
чтобы отношение четвертого слагаемого
разложения к третьему было равно
,
чтобы отношение четвертого слагаемого
разложения к третьему было равно
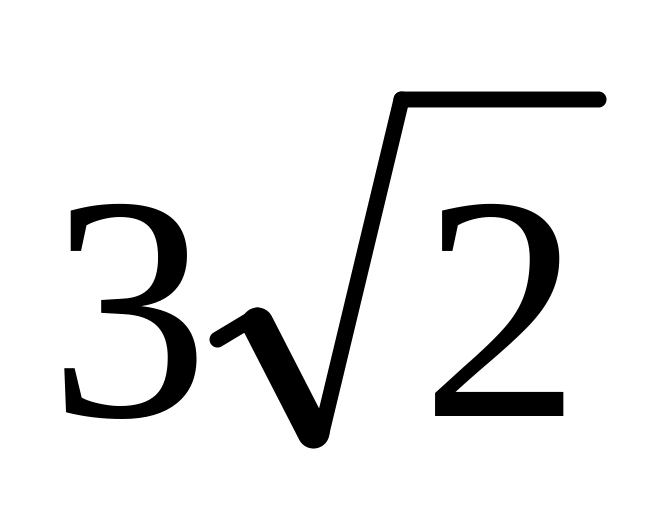 ?
?При каком значении x четвертое слагаемое разложения
 в 20 раз больше m, если
биномиальный коэффициент четвертого
слагаемого относится к биномиальному
коэффициенту второго слагаемого как
5:1?
в 20 раз больше m, если
биномиальный коэффициент четвертого
слагаемого относится к биномиальному
коэффициенту второго слагаемого как
5:1?Сумма коэффициентов второго и третьего слагаемых разложения
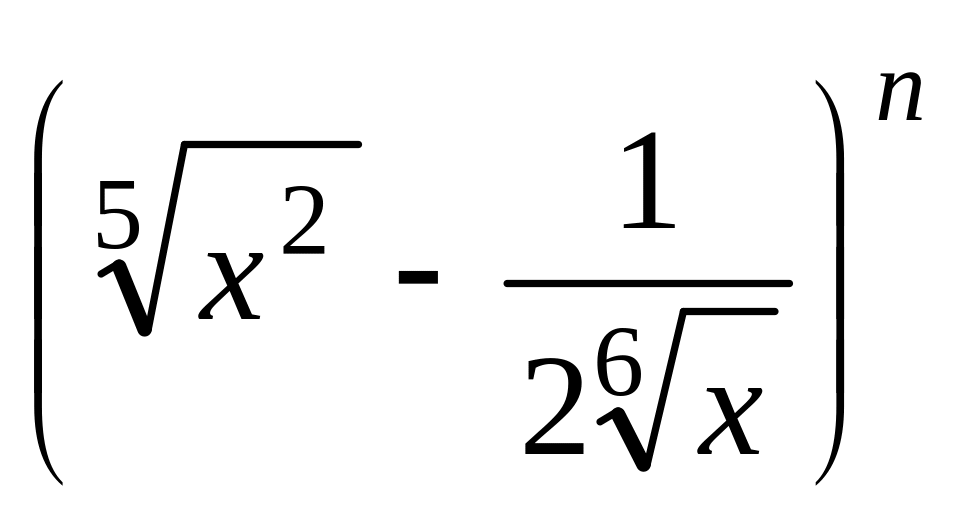 равна 25,5. Написать член, не содержащий
x.
равна 25,5. Написать член, не содержащий
x.Найти наибольший полиномиальный коэффициент разложения
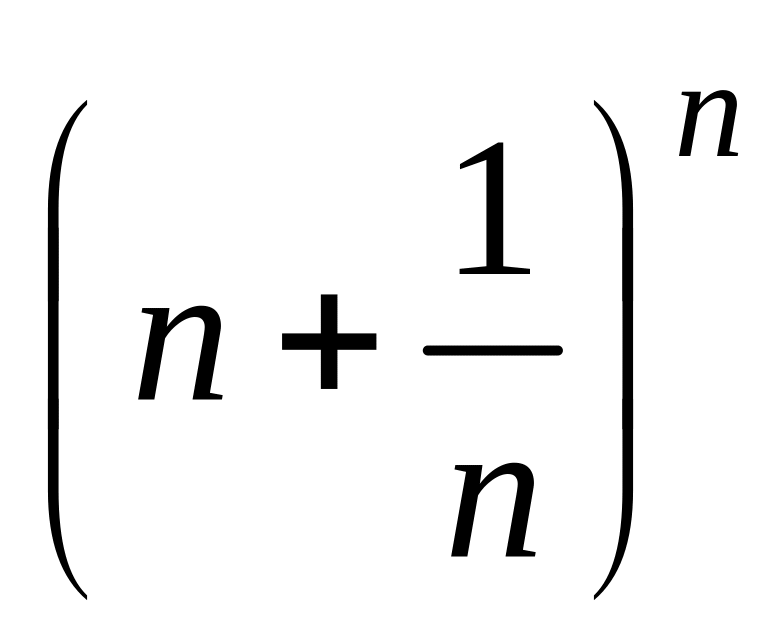 ,
если произведение четвертого от начала
и четвертого от конца слагаемых равно
14400?
,
если произведение четвертого от начала
и четвертого от конца слагаемых равно
14400?Разность между третьими биномиальными коэффициентами разложений
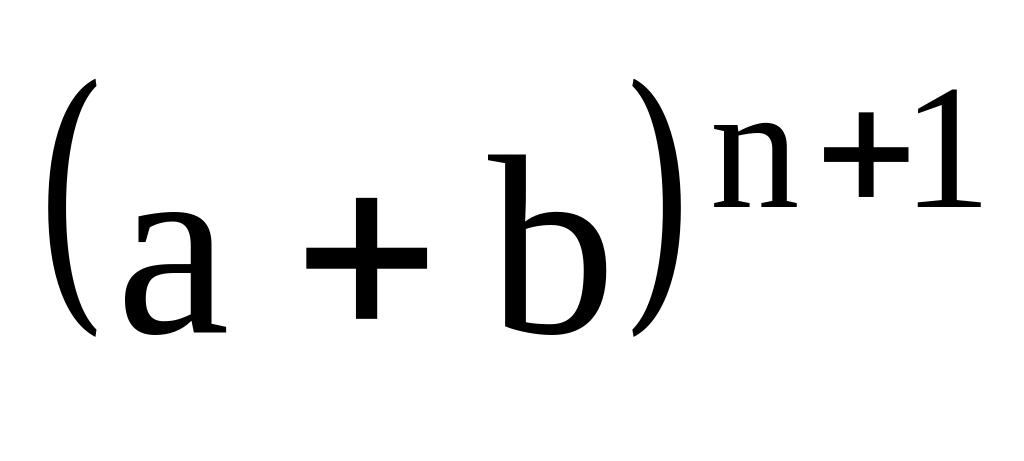 и
и
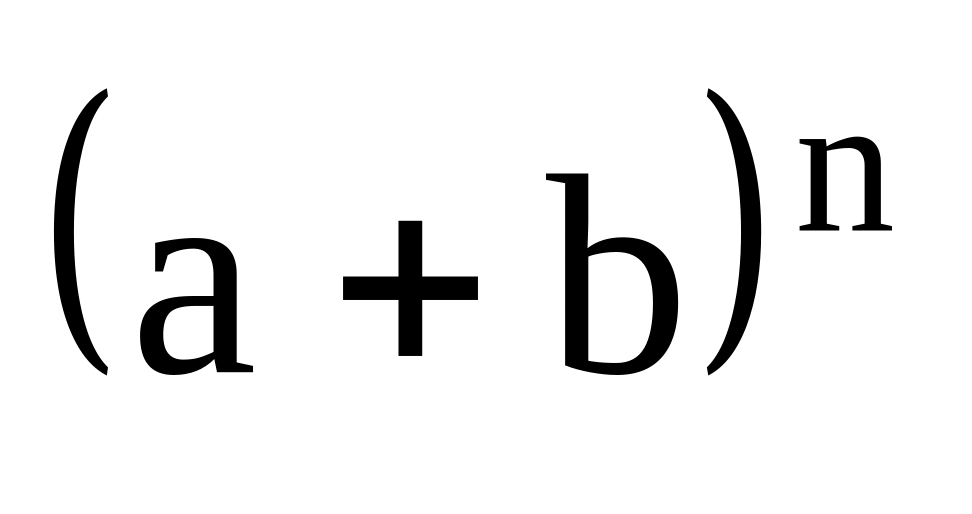 равна 225. Найти число рациональных
членов разложения
равна 225. Найти число рациональных
членов разложения
 .
.Сумма третьего от начала и четвертого от конца биномиальных коэффициентов разложения
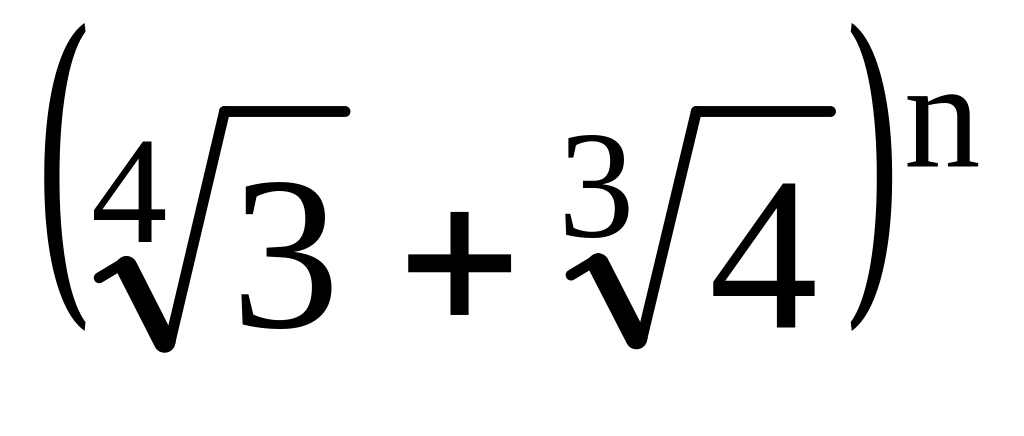 равна 9900. Сколько рациональных членов
содержится в этом разложении?
равна 9900. Сколько рациональных членов
содержится в этом разложении?При каких значениях x четвертое слагаемое разложения
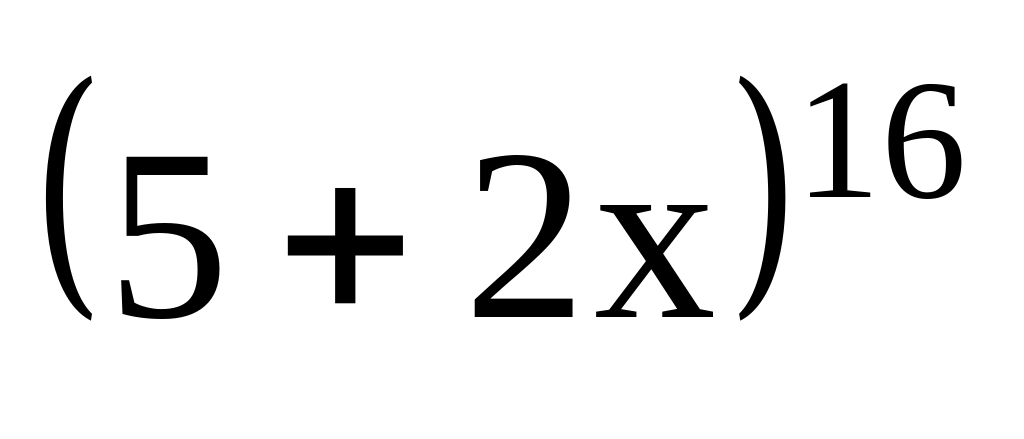 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых?Найти k-й член разложения
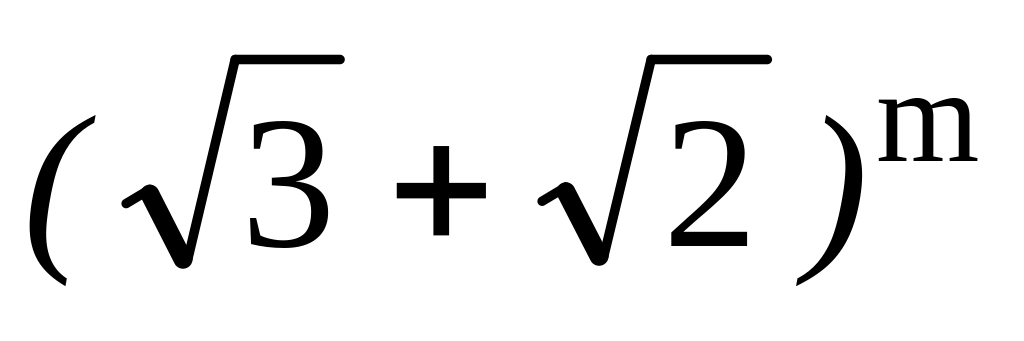 ,
если известно, что
,
если известно, что

Элементы математической логики
4.1 Основные понятия и формулы
Высказывание – это всякое утверждение, о котором имеет смысл говорить, что оно истинно или ложно.
В математической логике обычно истинность высказывания обозначается 1, ложность – 0.
Высказывания, истинные (ложные) во всех возможных ситуациях, называются абсолютно истинными (абсолютно ложными). Абсолютно истинные и абсолютно ложные высказывания называются логическими константами.
Одноместная логическая операция – отрицание: отрицание истинного ложно и наоборот (таблица 2). Отрицание - одноместная операция в том смысле, что из одного простого высказывания А строится новое высказывание А или А (читается: не А).
Таблица 2 - Таблица истинности операции отрицания
-

0
1
1
0
Все остальные логические операции являются двуместными: сложное высказывание строится из двух или более простых.
Конъюнкция (логическое умножение): высказывание АВ (читается: А и В) истинно тогда и только тогда, когда истинны оба высказывания А и В (таблица 3).
Таблица 3 - Таблица истинности операции конъюнкции
-
0
0
0
0
1
0
1
0
0
1
1
1
Дизъюнкция (логическое сложение) высказываний А и В - высказывание АВ (читается: А или В), которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний А или В (таблица 4).
Таблица 4 - Таблица истинности операции дизъюнкции
-
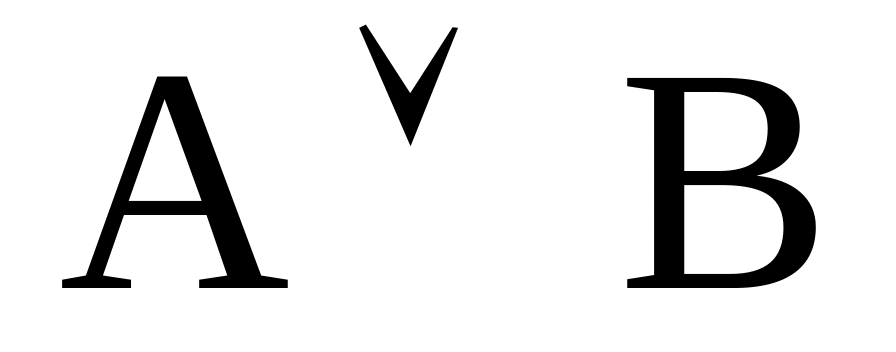
0
0
0
0
1
1
1
0
1
1
1
1
Альтернативная дизъюнкция (сложение
по модулю 2) высказываний А и В -
высказывание А![]() В
(читается: или А, или В), которое истинно
тогда и только тогда, когда истинно
только одно из высказываний А или В
(таблица 5).
В
(читается: или А, или В), которое истинно
тогда и только тогда, когда истинно
только одно из высказываний А или В
(таблица 5).
Таблица 5 - Таблица истинности операции альтернативной дизъюнкции
-
0
0
0
0
1
1
1
0
1
1
1
0
Импликация высказываний А и В - высказывание АВ (читается: если А, то В), которое ложно тогда и только тогда, когда А истинно, а В ложно (таблица 6). А называется посылкой, В – следствием.
Таблица 6 - Таблица истинности операции импликации
-
0
0
1
0
1
0
1
0
1
1
1
1
Эквивалентность высказываний А и
В - высказывание А![]() В
(читается А эквивалентно В), которое
истинно тогда и только тогда, когда А и
В оба истинны или оба ложны (таблица 7).
В
(читается А эквивалентно В), которое
истинно тогда и только тогда, когда А и
В оба истинны или оба ложны (таблица 7).
Таблица 7 - Таблица истинности операции эквивалентности
-
0
0
1
0
1
0
1
0
0
1
1
1
Штрихом Шеффера или антиконъюнкцией
называется логическая операция,
определяемая формулой
![]() .
.
Стрелкой Пирса или антидизъюнкцией
называется логическая операция,
определяемая формулой
![]() .
.
Функцией алгебры логики от n переменных х1,x2,...,xn называется функция f(x1,x2,...,xn), принимающая значения 0 или 1, аргументы которой также принимают значения 0 или 1.
Функция алгебры логики f(x1,x2,...,xn) может задаваться своей таблицей истинности, в каждой строке которой дается набор длины n значений логических переменных x1,x2,...,xn и соответствующее значение функции алгебры логики.
Всего возможных наборов n логических переменных равно N=2n.
Всего функций алгебры логики от n логических переменных равно 2N, где N=2n.
Функции f и g алгебры логики от n логических переменных x1,x2,...,xn называются равносильными (f=g), если при каждом возможном наборе логических переменных значения f и g равны (таблицы истинности функций совпадают).
Если f(x)=0, то говорят, что f тождественно равна 0.
Если f(x)=1, то говорят, что f тождественно равна 1.
В алгебре логики знак конъюнкции (логическое умножение) обычно опускается: xy=xy.
Важнейшие равносильности алгебры логики:

Суперпозиция основных логических
функций
![]()
называется формулой.
Введем обозначение:
![]()
Формула
![]() ,
где
,
где
![]() любой двоичный набор, а среди переменных
любой двоичный набор, а среди переменных
![]() могут быть совпадающие, называется
элементарной конъюнкцией.
могут быть совпадающие, называется
элементарной конъюнкцией.
Всякая дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).
Элементарная конъюнкция называется правильной, если в нее каждая переменная входит не более одного раза, включая ее вхождение под знаком отрицания.
Правильная элементарная конъюнкция называется полной относительно переменных x1,x2,...,xn, если в нее каждая из этих переменных входит один и только один раз, быть может, со знаком отрицания.
Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных x1,x2,...,xn называется полная правильная ДНФ, в которой нет одинаковых элементарных конъюнкций.
Всякую функцию алгебры логики f(x1,x2,...,xn), не равную тождественно нулю, можно представить совершенной дизъюнктивной нормальной формой:
![]() ,
,
где символ
![]() означает, что дизъюнкция берется по тем
наборам, на которых функция равна 1.
означает, что дизъюнкция берется по тем
наборам, на которых функция равна 1.
Формула вида
![]() называется элементарной дизъюнкцией.
называется элементарной дизъюнкцией.
Всякая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ).
Элементарная дизъюнкция называется правильной, если в нее каждая переменная входит не более одного раза, включая ее вхождение под знаком отрицания.
Правильная элементарная дизъюнкция называется полной относительно переменных x1,x2,...,xn, если каждая из этих переменных входит в нее один и только один раз, быть может, со знаком отрицания.
Совершенной конъюнктивной нормальной формой (СКНФ) относительно переменных x1,x2,...,xn называется полная, правильная КНФ, в которой нет одинаковых элементарных дизъюнкций.
Всякую функцию алгебры логики f(x1,x2,...,xn), не равную тождественно 1, можно представить совершенной конъюнктивной нормальной формой:
![]() ,
,
где символ
![]() означает, что конъюнкция берется по тем
наборам, на которых функция равна нулю.
означает, что конъюнкция берется по тем
наборам, на которых функция равна нулю.
Для упрощения ДНФ или КНФ рекомендуется применять следующие равносильности: