1 Основы теории множеств

1.1 Основные понятия и операции

Множество - это любая определенная совокупность объектов, которые называются элементами множества. Элементы множества различны и отличимы друг от друга.

Приняты следующие обозначения. Если a - элемент множества А, то пишут: а А. В противном случае: а А или а А.

Два множества А и В равны, если они содержат одни и те же элементы: А=В.

Множество А всех элементов, обладающих свойством Н(x), обозначается А= или А= .

Множество, не содержащее ни одного элемента, называется пустым и обозначается .

Если все элементы множества В являются элементами множества А, то это обозначают В А или А В (В содержится в А или А содержит В). Множество В называется подмножеством множества А. Если В А, то В называется собственным подмножеством множества и обозначается: В А. Считается, что  является подмножеством любого множества.

Отношения и называются включением и собственным включением.

Объединение множеств А и В обозначается А В и представляет собой множество элементов, принадлежащих или множеству А, или множеству В.

Пересечение множеств А и В обозначается А В и представляет собой множество элементов, принадлежащих и множеству А, и множеству В (их общая часть).

Если множества А и В не имеют общих элементов, то есть их пересечение есть пустое множество: А В=, то они называются непересекающимися или дизъюнктными.

Справедливы следующие соотношения:

;

;

;

, ;

;

=А, =.

Разность множеств А и В обозначается А\В, это есть множество элементов множества А, которые не принадлежат множеству В.

Симметрическая разность АВ множеств А и В представляет собой множество, состоящее из элементов, принадлежащих в точности одному из множеств А и В: АВ=(А\В)(В\А).

Если А U, то дополнение множества А относительно множества U определяется как =U\А.

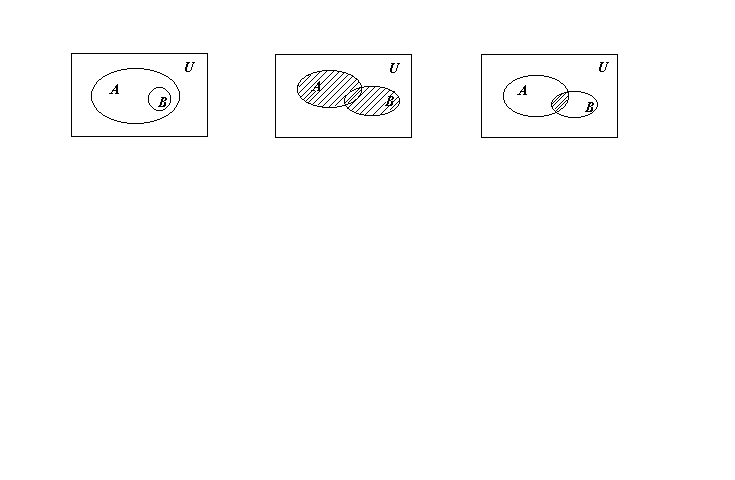
Для более наглядного представления операций над множествами и их свойств применяют диаграммы Эйлера - Венна (рисунок 1). Каждое множество предсталяется множестом точек на плоскости.

\

Рисунок 1 – Диаграммы Эйлера – Венна

Приняты следующие обозначения для числовых множеств:

N – множество натуральных чисел;

Z – множество целых чисел;

R – множество действительных чисел;

Q – множество рациональных чисел;

С – множество комплексных чисел.

Множества А и В называются эквивалентными или равномощными (АВ), если между ними можно установить взаимно однозначное соответствие.

Множество А является бесконечным, если оно эквивалентно некоторому собственному подмножеству.

Всякое бесконечное множество, эквивалентное множеству натуральных чисел N, называется счетным.

Всякое бесконечное множество, эквивалентное множеству действительных чисел Q, называется множеством мощности континуума. Мощность континуума обозначается через .

Множество А, состоящее из конечного числа n элементов, называется конечным. Мощность конечного множества А равна: А=n.

Если АВ, то АВ=А+В - АВ.

Для дизъюнктных множеств (АВ= ) АВ=А+В.

Пусть A_i (i =1,2,...,n; n>1) – конечные множества. Имеет место формула включений-исключений:

А₁А₂...А_n=(A₁+A₂+...+A_n) – ...

... - (A₁A₂+A₁A₃+...+A_n-1A_n) +...

...+ (A₁A₂A₃+A₁A₂A₄+...+A_n-2A_n-1A_n) -- ...

...+(-1)ⁿ⁺¹A₁A₂...A_n.

Универсальным множеством U по отношению к конечному множеству А называется множество всех подмножеств множества А. Мощность универсального множества U равна U=2ⁿ, где n=A.